
Ce que cet article vous apporte concerne le calcul de statistiques simples en Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.
1. Pour ces opérations, assurez-vous que la bibliothèque intégrée Anaconda a été installée sur l'ordinateur. Si une erreur se produit après l'installation, vous pouvez désinstaller Python sur l'ordinateur d'origine et réinstaller Anaconda. recommandé lors de l'installation Cochez directement Ajouter des variables d'environnement, sinon vous devrez ajouter vous-même des variables d'environnement à l'avenir Dans le compilateur de Pycharm, sélectionnez python dans le dossier d'installation d'Anaconda. Créez un nouveau dossier de données dans Pycharm pour stocker les fichiers de données.
2. Ouvrez la console Python.
3. Utilisez d'abord python pour lire les données. Vous devez d'abord saisir import pandas as pd pour introduire le package pandas, puis saisir df=pd.read_csv("./data/CityData.csv") pour lisez les données, et enfin entrez df pour afficher les données.
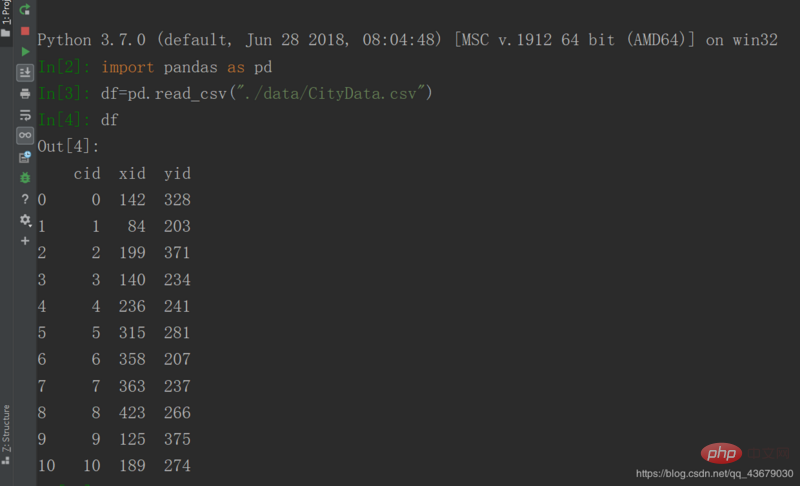
4. Entrez respectivement type(df) et type(df["cid"]) pour constater que les deux types de données sont différents.


5. Calculer la moyenne : df.mean() ou df["xid"].mean()
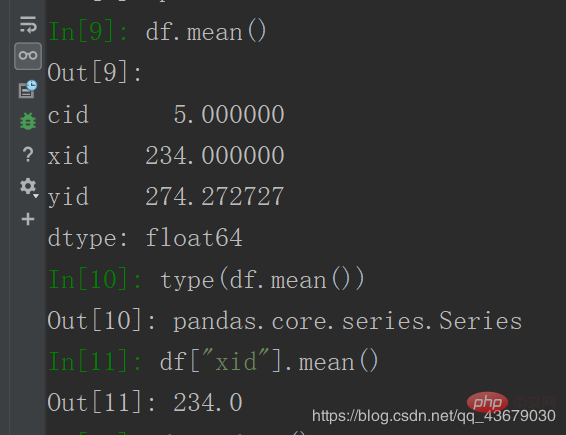
6. Calculez la médiane : saisissez df.median( ) ou df["yid"].median

7. Rechercher des quartiles : saisissez df .quantile(q =0,25)

8. Recherchez le mode : entrez df.mode() ou df["xid"].mode( )
9. Trouvez l'écart type : entrez df.std() ou df["yid"].std()
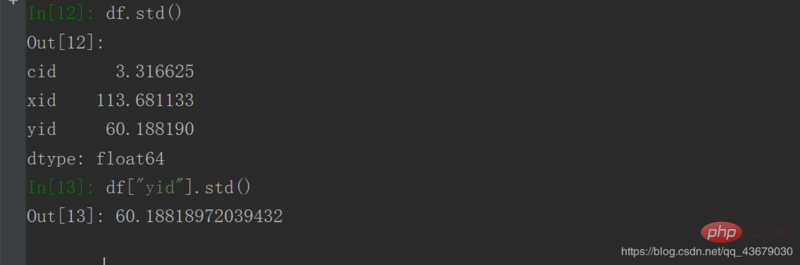
10. Calculer la variance : df.var() ou df["xid"].var()

11. df["xid"].sum()
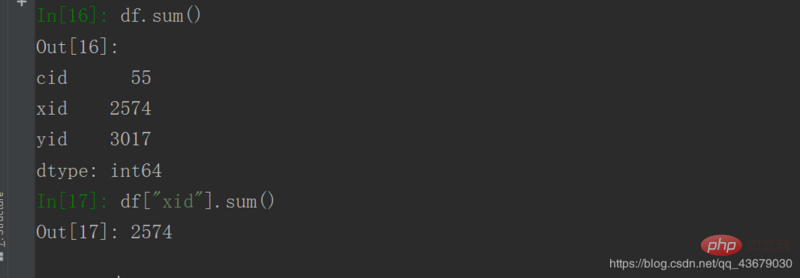
12. Calculez le coefficient d'asymétrie : df.skew() ou df[ "yid"] .skew()
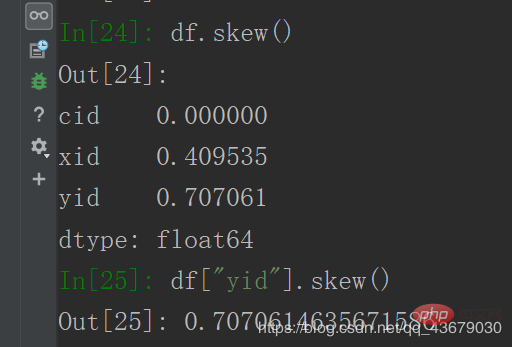
13. Calculer le coefficient d'aplatissement : df.kurt() ou df["yid"].kurt ()
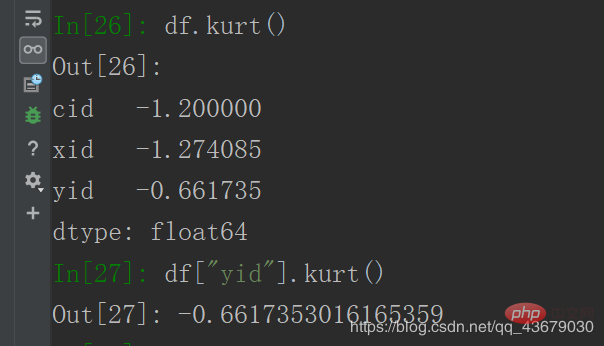
14. Générez une fonction de distribution normale. Les pandas ne peuvent pas la générer directement. Vous devez d'abord introduire scipyimport scipy.stats en tant que ss, puis entrer la norme ss. , ce qui est généré à ce moment est un objet distribué normal. Nous entrons ss.norm.stats(moments="mvsk") pour vérifier respectivement la moyenne, la variance, le coefficient d'asymétrie et le coefficient d'aplatissement.

A ce moment, nous pouvons voir que quatre valeurs sont générées, correspondant au mvsk de la distribution normale, qui sont 0, 1, 0 et 0 respectivement.
15.ss.norm.pdf(0.0) représente la valeur de l'ordonnée lorsque l'abscisse est 0. ss.norm.ppf(0.9) signifie que la valeur obtenue lors de l'accumulation depuis l'infini négatif jusqu'à la valeur de retour est de 0,9, où la valeur après ppf doit être comprise entre 0 et 1. ss.norm.cdf(2) représente la valeur de retour lors de l'intégration de l'infini négatif à 2, et ss.norm.rvs(size=10) peut obtenir 10 nombres aléatoires conformes à la distribution normale.
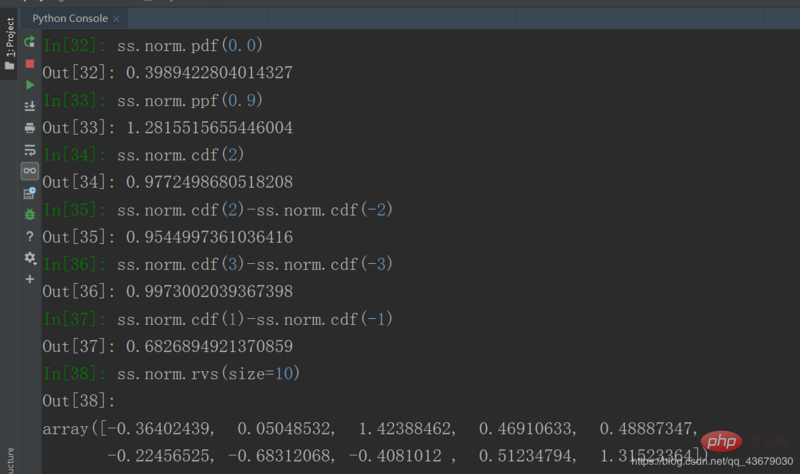
16. De même, nous pouvons saisir ss.chi2 et ss.t pour obtenir respectivement la distribution du chi carré et la distribution T.

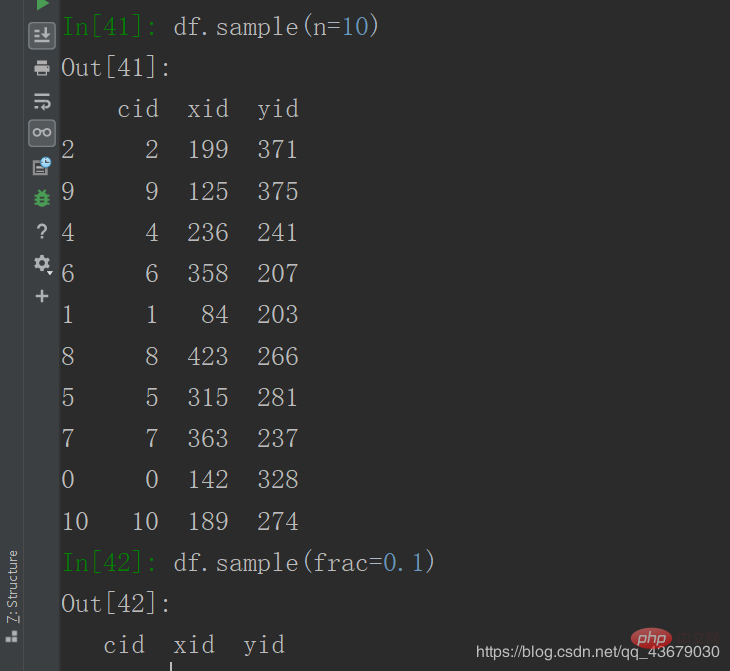
17. De plus, nous pouvons également effectuer un échantillonnage, entrez df.sample(n=10) pour extraire 10 échantillons des données, entrez df. sample(frac=0.1) prélève un échantillon de 10 % des données.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!