
Cet article vous apporte une introduction détaillée aux fonctions couramment utilisées dans numpy de Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.
Numpy est une bibliothèque liée au calcul scientifique en Python. Cet article présentera certaines fonctions numpy couramment utilisées. Vous devez les présenter avant d'utiliser numpy. Entrez import numpy comme np. np.
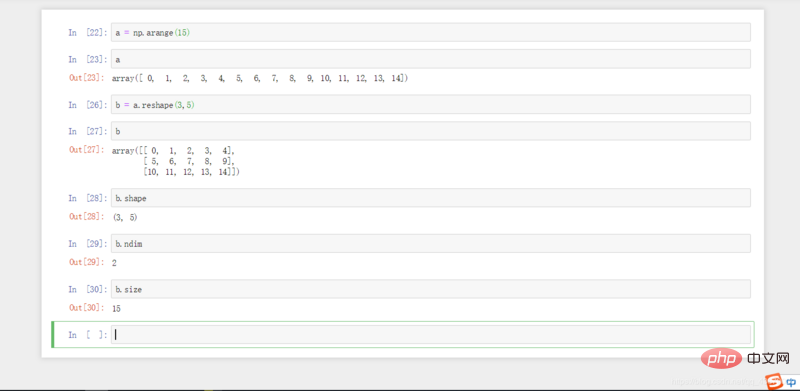
1.np.arange(n) : Génère des entiers de 0 à n-1.
2.a.reshape(m,n) : Redéfinir a comme une matrice avec m lignes et n colonnes.
3.a.shape : Imprime les lignes et les colonnes de a.
4.a.ndim : Trouver les dimensions d'un.
5.a.size : affiche le nombre d'éléments dans a.
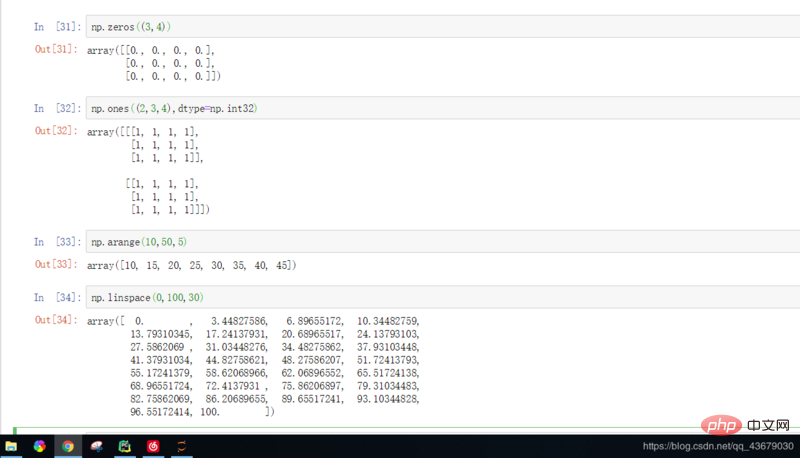
6.np.zeros((m,n)) : Génère une matrice nulle de m lignes et n colonnes. dans la fonction Un tuple est transmis. La matrice 0 générée à ce moment est suivie d'un point décimal, car le type de données par défaut du système est à virgule flottante. Pour obtenir le type entier, nous devons spécifier le type de données à l'avance.
7.np.ones((k,m,n),dtype=np.int32) : Générez k matrices d'identité avec m lignes et n colonnes, et le type de données dans la matrice est entier.
8.np.arange(m,n,k) : Générez des données découpées de m à n avec un pas de k.
9.np.linspace(m,n,k) : Prenez k valeurs à intervalles égaux dans les données de m à n.
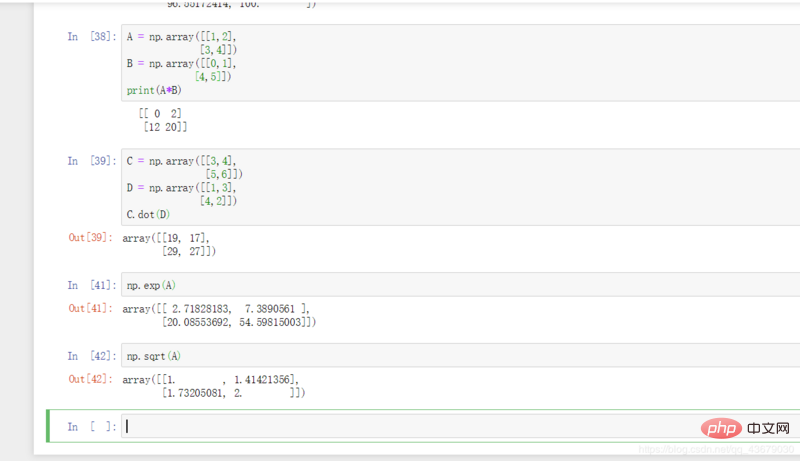
10. Si A et B sont des matrices de même dimension, alors A*B renvoie le résultat de la multiplication des positions correspondantes de A et B matrices , A.dot(B) ou np.dot(A,B) renvoie le résultat de la multiplication matricielle.
11.np.exp(A) ou np.sqrt(B) : obtenez respectivement la puissance B de e et le résultat de la racine carrée de chaque nombre de la matrice B.
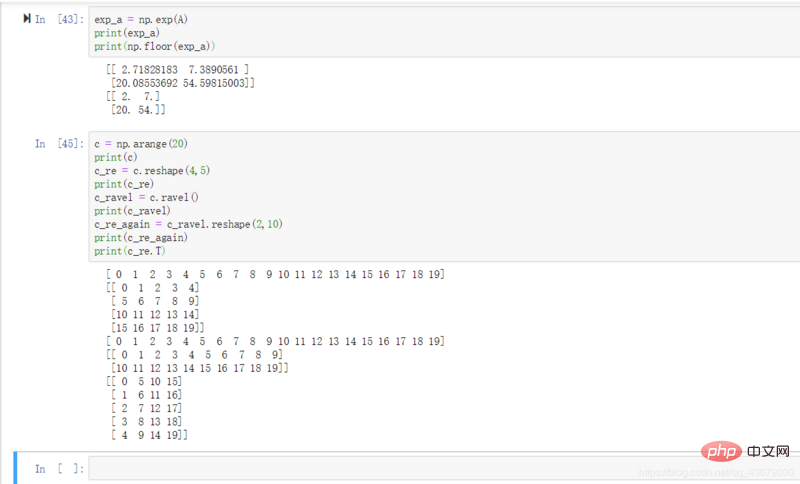
12.np.floor() : arrondir à l'inférieur.
13.a.ravel() : Ré-étire la matrice a en un vecteur Après étirement, elle peut être remodelée en une nouvelle matrice.
14.a.T : Trouver la matrice de transposition de a.
15.a.reshape(n,-1) ou a.reshape(-1,n) : Après avoir déterminé les lignes (colonnes) d'une matrice, les colonnes (lignes) correspondantes sont également directement déterminées, alors entrez simplement -1.
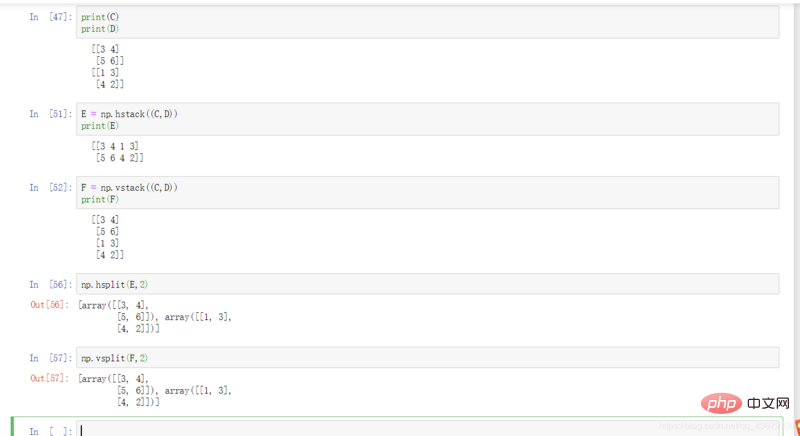
16.np.hstack((a,b)) : Épisser les matrices a et b horizontalement.
17.np.vstack((a,b)) : Épisser les matrices a et b verticalement.
18.np.hsplit(a,n) : Couper la matrice a en n parties latéralement.
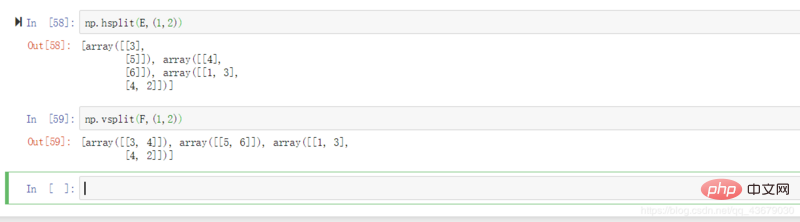
19.np.hsplit(a,(m,n)) : Divisé horizontalement dans l'espace entre l'index m et n de a.
20.np.vsplit(a,n) : Coupez la matrice a en n parties verticalement.
21.np.hsplit(a,(m,n)) : Coupe verticalement dans l'espace avec les index m et n dans a.
22. Copie de la matrice :
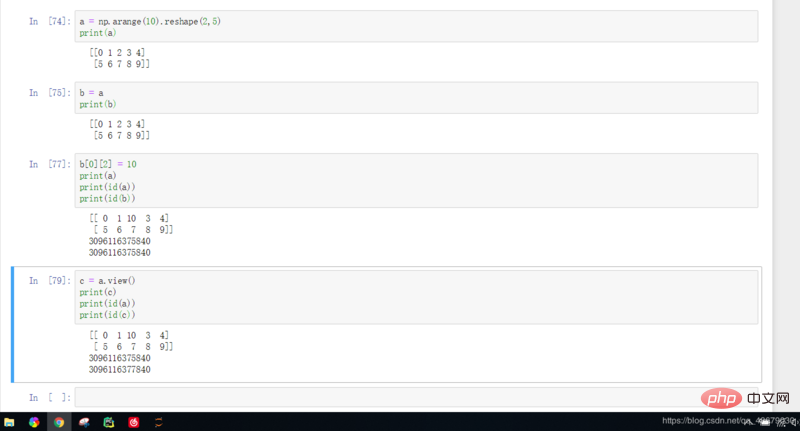
b = a : Les adresses de b et a obtenues à ce moment sont exactement les mêmes, c'est-à-dire que a et b sont simplement des noms différents de la même matrice, et opérer sur l'une d'entre elles entraînera le même changement dans l'autre matrice.
b = a.view() : L'adresse de b obtenue à ce moment est différente de celle de a, mais l'opération sur b changera a.
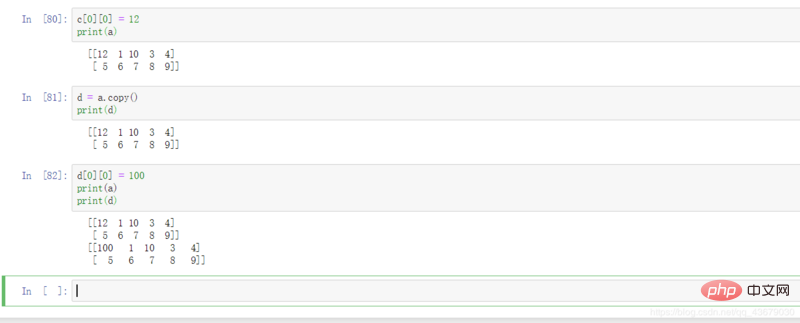
b = a.copy() : Ce que vous obtenez à ce moment, ce sont deux matrices complètement indépendantes.
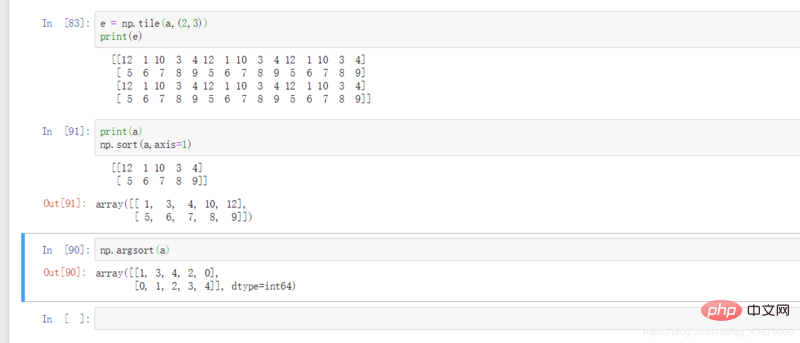
23.b = np.tile(a,(m,n )) : Augmentez le nombre de lignes de la matrice a de m fois et le nombre de colonnes de n fois.
24.np.sort(a, axis=k) : Trier la matrice a en k dimension.
25.np.argsort(a) : renvoie la valeur d'index de a par ordre croissant (l'arrangement par défaut est l'ordre croissant).
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!