Exemple de code d'implémentation Java du tri radix (RadixSort)

Ce que cet article vous apporte est un exemple de code pour implémenter le tri par base (RadixSort) en Java. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.

Le tri par base est un dérivé du tri par seau et du tri par comptage, car l'un de ces deux types est utilisé dans le tri par base.

Les éléments à trier par tri radix doivent avoir des chiffres hauts et bas. Par exemple, les mots adobe, activiti et activiti sont supérieurs à adobe.

Maintenant on peut se poser une question, comment trier les mots dans le dictionnaire ?

Par exemple, nous avons maintenant les mots suivants :

"Java", "Mongodb", "Redis", "Kafka", "javascript", "mysql", "mybatis", "kindle", "rpc", "Algorithm", "mergeSort", "quickSort", "Adobe"

Comment le trier ici ? hauteur. Les bits sont divisés en individus individuels. Par exemple, Adobe est divisé en A, d, o, b, e, l'algorithme est divisé en A, l, g, o, r, i, t, h, m, puis nous procédons de droite à gauche, afin de comparer. Mais Adobe et Algorithm ne peuvent pas être comparés directement ici car ils sont de longueur différente, donc avant la comparaison, nous devons trouver la longueur de l'élément le plus long, puis compléter les éléments courts restants à la même longueur :

Adobe0000

Algorithme

De cette façon, une comparaison peut être formée, de droite à gauche, 0:m,0:h,0:t,0:i,e:r,b:o,o : g,d:l,A:A, nous pouvons comparer Adobe Algorihtm

Suivre les images suivantes rendra le principe plus clair :

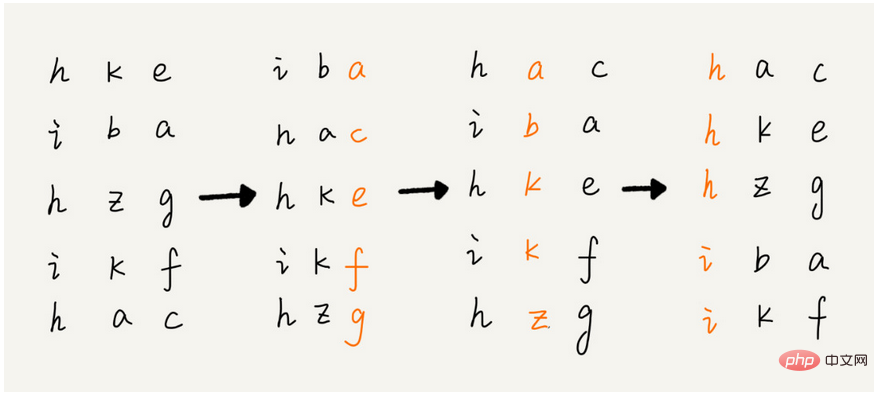
De We peut voir sur la figure ci-dessus que le tri par base sera comparé de droite à gauche (c'est-à-dire qu'il doit être parcouru plusieurs fois dans la mise en œuvre de notre programme), et le nombre spécifique de parcours dépend de la longueur de l'élément le plus long, de droite à gauche. Le tri par compartiment ou le tri par comptage peut être utilisé pour comparer les éléments de chaque bit de gauche. La complexité temporelle du tri par compartiment et du tri par comptage est O(n). O(n). (k * n), et k n'est généralement pas très grand et peut être considéré comme une constante, donc la complexité temporelle du tri par base est également O(n).

Ce qui suit est mon implémentation Java :

package com.structure.sort;
/**
 * @author zhangxingrui
 * @create 2019-01-30 14:58
 **/
public class RadixSort {
    public static void main(String[] args) {
        /*int[] numbers = {19, 36, 24, 10, 9, 29, 1, 0, 3, 60, 100, 1001, 999, 520, 123, 96};
        radixSort(numbers);
        for (int number : numbers) {
            System.out.println(number);
        }*/
        String[] words = {"Java", "Mongodb", "Redis", "Kafka", "javascript", "mysql", "mybatis", "kindle", "rpc", "Algorithm", "mergeSort", "quickSort", "Adobe"};
//        String[] words = {"Java", "mongodb", "Kafka"};
        radixSort(words);
        for (String word : words) {
            System.out.println(word.replaceAll("0", ""));
        }
    }
    /**
     * @Author: xingrui
     * @Description: 基数排序（单词）
     * @Date: 15:53 2019/1/30
     */
    private static void radixSort(String[] words){
        int exp = 0;
        int maxLength = getMaxLength(words);
        autoComplete(words, maxLength);
        for(exp = 1; exp <= maxLength; exp++){
            countingSort(words, exp);
        }
    }
    /**
     * @Author: xingrui
     * @Description: 计数排序（单词）
     * @Date: 13:57 2019/1/30
     */
    private static void countingSort(String[] words, int exp){
        int n = words.length;
        String[] r = new String[n];
        int[] c = new int[122];
        for(int i = 0; i < n; ++i){
            int asc = (byte)words[i].charAt(words[i].length() - exp);
            c[asc]++;
        }
        for(int i = 1; i < 122; ++i){
            c[i] = c[i-1] + c[i];
        }
        for (int i = n - 1; i >= 0; --i){
            int asc = (byte)words[i].charAt(words[i].length() - exp);
            int index = c[asc];
            r[index - 1] = words[i];
            c[asc]--;
        }
        for(int i = 0; i < n; ++i){
            words[i] = r[i];
        }
    }
    /**
     * @Author: xingrui
     * @Description: 基数排序（纯数字）
     * @Date: 15:00 2019/1/30
     */
    private static void radixSort(int[] numbers){
        int exp = 0;
        int maxNumber = getMaxNumber(numbers);
        for(exp = 1; maxNumber/exp > 0; exp *= 10){
            countingSort(numbers, exp);
        }
    }
    /**
     * @Author: xingrui
     * @Description: 计数排序（纯数字）
     * @Date: 13:57 2019/1/30
     */
    private static void countingSort(int[] numbers, int exp){
        int n = numbers.length;
        int[] r = new int[n];
        int[] c = new int[10];
        for(int i = 0; i < n; ++i){
            c[numbers[i]/exp % 10]++;
        }
        for(int i = 1; i < 10; ++i){
            c[i] = c[i-1] + c[i];
        }
        for (int i = n - 1; i >= 0; --i){
            int index = c[numbers[i] / exp % 10];
            r[index - 1] = numbers[i];
            c[numbers[i] / exp % 10]--;
        }
        for(int i = 0; i < n; ++i){
            numbers[i] = r[i];
        }
    }
    /**
     * @Author: xingrui
     * @Description: 自动补全单词
     * @Date: 16:38 2019/1/30
     */
    private static void autoComplete(String[] words, int maxLength){
        int i = 0;
        for (String word : words) {
            if(word.length() < maxLength){
                int value = maxLength - word.length();
                StringBuilder sb = new StringBuilder();
                for(int j = 0; j < value; ++j){
                    sb.append("0");
                }
                words[i] = word + sb;
            }
            i++;
        }
    }
    /**
     * @Author: xingrui
     * @Description: 获取字符串最大的长度
     * @Date: 15:56 2019/1/30
     */
    private static int getMaxLength(String[] words){
        int maxLength = words[0].length();
        for(int i = 1; i < words.length; ++i){
            if(words[i].length() > maxLength)
                maxLength = words[i].length();
        }
        return maxLength;
    }
    /**
     * @Author: xingrui
     * @Description: 获取最大的数字
     * @Date: 15:56 2019/1/30
     */
    private static int getMaxNumber(int[] numbers){
        int maxNumber = numbers[0];
        for(int i = 1; i < numbers.length; ++i){
            if(numbers[i] > maxNumber)
                maxNumber = numbers[i];
        }
        return maxNumber;
    }
}

Ce qu'il faut noter, c'est qu'avant de trier, vous devez trouver la longueur maximale de l'élément pour déterminer le nombre de boucles et compléter les éléments plus courts. basé sur la longueur maximale de l'élément.

Résultat de l'exécution du programme :

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!