
Le contenu de cet article explique comment utiliser Python pour calculer pi (exemple de code). Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer.
1. Introduction à π
Introduction à π
Pi est représenté par la lettre grecque π (prononcée pài), qui est une constante ( approximativement égal à 3,141592654), qui représente le rapport entre la circonférence et le diamètre d'un cercle. Il s'agit d'un nombre décimal infini et non répétitif. Dans la vie quotidienne, 3,14 est généralement utilisé pour représenter pi pour les calculs approximatifs.
Le processus de résolution de π
En 1965, le mathématicien britannique John Wallis a publié une monographie mathématique dans laquelle il a dérivé une formule et a découvert que pi est égal à l'infini, le produit de fractions multipliées ensemble.
En 2015, des scientifiques de l'Université de Rochester ont découvert la même formule pour pi dans les calculs de mécanique quantique des niveaux d'énergie des atomes d'hydrogène.
Le 14 mars 2019, Google a annoncé que pi avait désormais atteint 31 400 milliards de décimales.
Ici, j'utilise une formule que je considère comme « bonne » à résoudre. Bonne car les résultats du calcul sont relativement précis, mais le processus de calcul prend beaucoup de temps. Apprenons ensemble. 2. Calcul approximatif de π
1. Formule de calcul
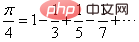 2. Explication de la méthode
2. Explication de la méthode
Les numérateurs à droite de l'équation sont tous 1, et le dénominateur C'est une séquence croissante, à partir du premier élément, le signe des termes impairs est positif et le signe des termes pairs est négatif. Plus le dénominateur du côté droit de l’équation est grand et petit, plus la valeur calculée de pi est précise. En d’autres termes, plus il y a de termes sur le côté droit de l’équation, plus la valeur calculée est précise.
3. Implémentation du code (python)
4. Exemple d'imagefrom math import fabs #导入数学模块
from time import perf_counter #导入时间模块
def Bar(i): #动态文本条
N = pow(10,level)
a = int((i/N)*50)
b = 50 - a
Y , N = '*' * a , '.' * b
print("\r计算中:{:3.0f}% [{}->{}] {:.2f}s"
.format(2*a,Y,N,perf_counter()),end='')
level = eval(input('计算Pi精确到小数点后几位数:'))
print('\n{:=^70}'.format('计算开始'))
a,b,pi,tmp = 1,1,0,1
i = 0
'''
a 分子 | b 分母 | pi 圆周率
tmp 存储a/b的值 | i 执行进度
'''
perf_counter() #开始计时
while (fabs(tmp) >= pow(10,-level)): #计算Pi
pi += tmp
b += 2
a = -a
tmp = a/b
i += 2
Bar(i) #调用函数,实时显示计算进度
print('\n{:=^70}'.format('计算完成'))
print('\nPi的计算值为:{}'.format(round(pi*4,level))) #输出计算结果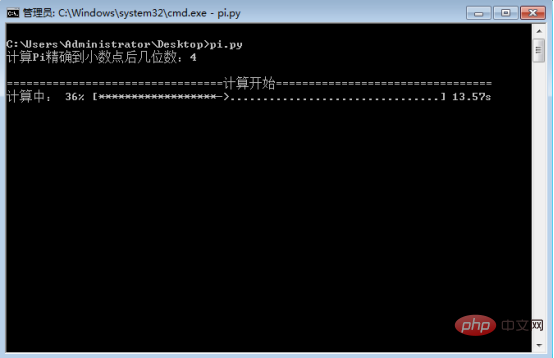

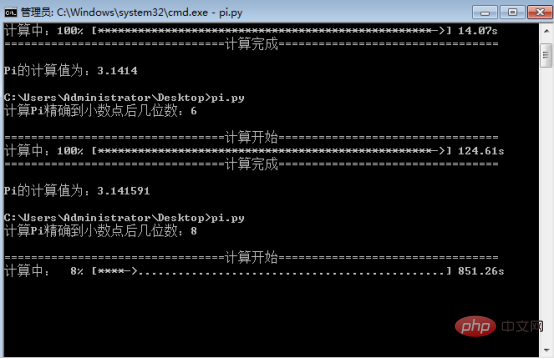 Comme le montrent les trois images ci-dessus, il ne faut que 14,07 secondes pour être précis à 4 décimales, 124,61 secondes pour être précis à 6 décimales et 850/8 % pour être précis. à 8 décimales = 10625 secondes, soit environ 177 minutes ou 2,95 heures. Cette méthode est bonne, mais son calcul prend quand même beaucoup de temps.
Comme le montrent les trois images ci-dessus, il ne faut que 14,07 secondes pour être précis à 4 décimales, 124,61 secondes pour être précis à 6 décimales et 850/8 % pour être précis. à 8 décimales = 10625 secondes, soit environ 177 minutes ou 2,95 heures. Cette méthode est bonne, mais son calcul prend quand même beaucoup de temps.
"Pi" est une existence merveilleuse et belle. C'est une décimale infinie et non répétitive. C'est comme une sorte de beauté imparfaite, tant que vous avez les yeux pour découvrir la beauté !
En 2011, l'Association mathématique internationale a officiellement annoncé que le 14 mars de chaque année serait la Journée internationale des mathématiques. La source est le pi de l'ancien mathématicien chinois Zu Chongzhi.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!