 interface Web
interface Web
 js tutoriel
js tutoriel
 Introduction aux algorithmes JavaScript de parcours en profondeur d'abord (DFS) et de parcours en largeur en premier (BFS)
Introduction aux algorithmes JavaScript de parcours en profondeur d'abord (DFS) et de parcours en largeur en premier (BFS)
Introduction aux algorithmes JavaScript de parcours en profondeur d'abord (DFS) et de parcours en largeur en premier (BFS)
Cet article vous présente une introduction aux algorithmes JavaScript de traversée en profondeur (DFS) et en largeur (BFS). Il a une certaine valeur de référence. Les amis dans le besoin pourront s'y référer. vous avez aidé.
Contexte : lors du développement d'une page, nous rencontrons parfois cette exigence : parcourir un certain nœud dom sur la page pour trouver le nœud dom cible. Notre approche normale consiste à utiliser le sélecteur document.getElementById() , document. getElementsByName() ou document.getElementsByTagName(), mais dans cet article, nous recherchons les nœuds dom d'un point de vue algorithmique et comprenons en même temps les principes du parcours en profondeur d'abord (DFS) et du parcours en largeur d'abord (BFS).
Préparation
Supposons que la structure dom sur la page soit la suivante :
<div> <ul> <li> <a> <img src="/static/imghw/default1.png" data-src="" class="lazy" alt="Introduction aux algorithmes JavaScript de parcours en profondeur d'abord (DFS) et de parcours en largeur en premier (BFS)" > </a> </li> <li> <span></span> </li> <li> </li> </ul> <p></p> <button></button> </div>
Convertissons cette structure dom en arbre
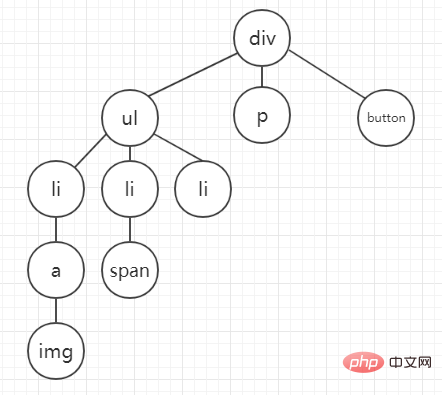
Après avoir fait cela, la structure dom semble être beaucoup plus claire.
Recherche en profondeur
Cette méthode parcourt l'arborescence DOM dans une dimension verticale, en commençant par un nœud DOM et en parcourant ses nœuds enfants jusqu'à ce que tous ses nœuds enfants aient été parcourus, ses nœuds frères sont traversés. Autrement dit, comme le montre la figure (l'ordre de parcours est la marque de verrouillage rouge) :
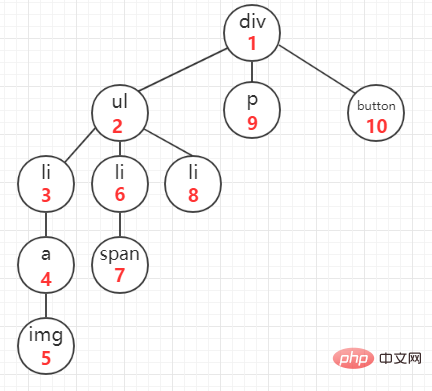
code js pour implémenter cet algorithme (version récursive) :
function deepFirstSearch(node,nodeList) {
if (node) {
nodeList.push(node);
var children = node.children;
for (var i = 0; i <p>Version non récursive : </p><pre class="brush:php;toolbar:false">function deepFirstSearch(node) {
var nodes = [];
if (node != null) {
var stack = [];
stack.push(node);
while (stack.length != 0) {
var item = stack.pop();
nodes.push(item);
var children = item.children;
for (var i = children.length - 1; i >= 0; i--)
stack.push(children[i]);
}
}
return nodes;
}deepFirstSearch accepte deux paramètres, le premier paramètre est le nœud qui doit être traversé, le second est le tableau stocké dans le nœud et renvoie le tableau après traversée, l'ordre des éléments du tableau C'est la séquence de traversée, méthode d'appel :
let root = document.getElementById('root')
deepTraversal(root,nodeList=[])Résultat de sortie de la console

Traversée en largeur en premier (traversée en largeur)
Cette méthode parcourt l'arborescence DOM dans une dimension horizontale, en commençant par le premier nœud enfant du nœud, en traversant tous ses nœuds frères, puis en traversant les nœuds enfants du premier nœud. Après avoir terminé la traversée, nous n'entrerons pas dans les détails pour le moment. Commence à parcourir les nœuds enfants de ses nœuds frères. Comme le montre la figure (l'ordre de parcours est la marque de verrouillage rouge) :
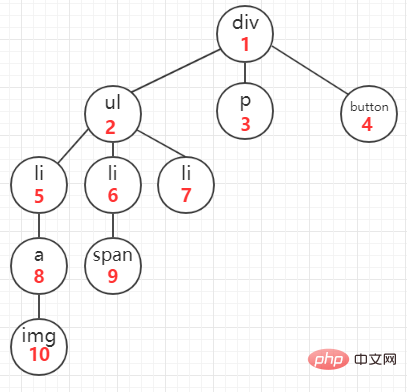
Code de l'algorithme d'implémentation js (version récursive) :
function breadthFirstSearch(node) {
var nodes = [];
var i = 0;
if (!(node == null)) {
nodes.push(node);
breadthFirstSearch(node.nextElementSibling);
node = nodes[i++];
breadthFirstSearch(node.firstElementChild);
}
return nodes;
}récursif version Parce que le niveau de BFS est trop profond, cela entraînera un débordement de pile : taille maximale de la pile d'appels dépassée, mais l'ordre de parcours ne pose toujours pas de problème. Vous pouvez opérer pendant le processus de parcours sans renvoyer le tableau parcouru.
Version non récursive :
function breadthFirstSearch(node) {
var nodes = [];
if (node != null) {
var queue = [];
queue.unshift(node);
while (queue.length != 0) {
var item = queue.shift();
nodes.push(item);
var children = item.children;
for (var i = 0; i <p>Sortie de la console : </p><p><img src="/static/imghw/default1.png" data-src="https://img.php.cn/upload/image/727/585/757/1553909199320348.png" class="lazy" title="1553909199320348.png" alt="Introduction aux algorithmes JavaScript de parcours en profondeur dabord (DFS) et de parcours en largeur en premier (BFS)"></p><p style="max-width:90%">Résumé : BFS et DFS sont tous deux des algorithmes graphiques. Premièrement, le La version décrite dans cet article est relativement simple et constitue un graphe non orienté et non connecté. D'autres algorithmes basés sur JavaScript seront mis à jour à l'avenir. </p><p style="white-space: normal;">Cet article est terminé ici. Pour d'autres contenus passionnants, vous pouvez prêter attention à la colonne <a href="http://www.php.cn/course/list/17.html" target="_blank">Tutoriel vidéo JavaScript</a> du site Web PHP chinois ! </p><p></p>Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
Écrit ci-dessus et compréhension personnelle de l'auteur : À l'heure actuelle, dans l'ensemble du système de conduite autonome, le module de perception joue un rôle essentiel. Le véhicule autonome roulant sur la route ne peut obtenir des résultats de perception précis que via le module de perception en aval. dans le système de conduite autonome, prend des jugements et des décisions comportementales opportuns et corrects. Actuellement, les voitures dotées de fonctions de conduite autonome sont généralement équipées d'une variété de capteurs d'informations de données, notamment des capteurs de caméra à vision panoramique, des capteurs lidar et des capteurs radar à ondes millimétriques pour collecter des informations selon différentes modalités afin d'accomplir des tâches de perception précises. L'algorithme de perception BEV basé sur la vision pure est privilégié par l'industrie en raison de son faible coût matériel et de sa facilité de déploiement, et ses résultats peuvent être facilement appliqués à diverses tâches en aval.
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
La couche inférieure de la fonction de tri C++ utilise le tri par fusion, sa complexité est O(nlogn) et propose différents choix d'algorithmes de tri, notamment le tri rapide, le tri par tas et le tri stable.
 L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
La convergence de l’intelligence artificielle (IA) et des forces de l’ordre ouvre de nouvelles possibilités en matière de prévention et de détection de la criminalité. Les capacités prédictives de l’intelligence artificielle sont largement utilisées dans des systèmes tels que CrimeGPT (Crime Prediction Technology) pour prédire les activités criminelles. Cet article explore le potentiel de l’intelligence artificielle dans la prédiction de la criminalité, ses applications actuelles, les défis auxquels elle est confrontée et les éventuelles implications éthiques de cette technologie. Intelligence artificielle et prédiction de la criminalité : les bases CrimeGPT utilise des algorithmes d'apprentissage automatique pour analyser de grands ensembles de données, identifiant des modèles qui peuvent prédire où et quand les crimes sont susceptibles de se produire. Ces ensembles de données comprennent des statistiques historiques sur la criminalité, des informations démographiques, des indicateurs économiques, des tendances météorologiques, etc. En identifiant les tendances qui pourraient échapper aux analystes humains, l'intelligence artificielle peut donner du pouvoir aux forces de l'ordre.
 Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
01Aperçu des perspectives Actuellement, il est difficile d'atteindre un équilibre approprié entre efficacité de détection et résultats de détection. Nous avons développé un algorithme YOLOv5 amélioré pour la détection de cibles dans des images de télédétection optique haute résolution, en utilisant des pyramides de caractéristiques multicouches, des stratégies de têtes de détection multiples et des modules d'attention hybrides pour améliorer l'effet du réseau de détection de cibles dans les images de télédétection optique. Selon l'ensemble de données SIMD, le mAP du nouvel algorithme est 2,2 % meilleur que YOLOv5 et 8,48 % meilleur que YOLOX, permettant ainsi d'obtenir un meilleur équilibre entre les résultats de détection et la vitesse. 02 Contexte et motivation Avec le développement rapide de la technologie de télédétection, les images de télédétection optique à haute résolution ont été utilisées pour décrire de nombreux objets à la surface de la Terre, notamment des avions, des voitures, des bâtiments, etc. Détection d'objets dans l'interprétation d'images de télédétection
 Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript : Comment obtenir le code d'état HTTP, des exemples de code spécifiques sont requis Préface : Dans le développement Web, l'interaction des données avec le serveur est souvent impliquée. Lors de la communication avec le serveur, nous devons souvent obtenir le code d'état HTTP renvoyé pour déterminer si l'opération a réussi et effectuer le traitement correspondant en fonction de différents codes d'état. Cet article vous apprendra comment utiliser JavaScript pour obtenir des codes d'état HTTP et fournira quelques exemples de codes pratiques. Utilisation de XMLHttpRequest
 Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
1. Contexte de la construction de la plateforme 58 Portraits Tout d'abord, je voudrais partager avec vous le contexte de la construction de la plateforme 58 Portraits. 1. La pensée traditionnelle de la plate-forme de profilage traditionnelle ne suffit plus. La création d'une plate-forme de profilage des utilisateurs s'appuie sur des capacités de modélisation d'entrepôt de données pour intégrer les données de plusieurs secteurs d'activité afin de créer des portraits d'utilisateurs précis. Elle nécessite également l'exploration de données pour comprendre le comportement et les intérêts des utilisateurs. et besoins, et fournir des capacités côté algorithmes ; enfin, il doit également disposer de capacités de plate-forme de données pour stocker, interroger et partager efficacement les données de profil utilisateur et fournir des services de profil. La principale différence entre une plate-forme de profilage d'entreprise auto-construite et une plate-forme de profilage de middle-office est que la plate-forme de profilage auto-construite dessert un seul secteur d'activité et peut être personnalisée à la demande. La plate-forme de mid-office dessert plusieurs secteurs d'activité et est complexe ; modélisation et offre des fonctionnalités plus générales. 2.58 Portraits d'utilisateurs de l'arrière-plan de la construction du portrait sur la plate-forme médiane 58
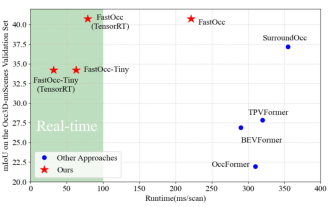 Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Écrit ci-dessus & La compréhension personnelle de l'auteur est que dans le système de conduite autonome, la tâche de perception est un élément crucial de l'ensemble du système de conduite autonome. L'objectif principal de la tâche de perception est de permettre aux véhicules autonomes de comprendre et de percevoir les éléments environnementaux environnants, tels que les véhicules circulant sur la route, les piétons au bord de la route, les obstacles rencontrés lors de la conduite, les panneaux de signalisation sur la route, etc., aidant ainsi en aval modules Prendre des décisions et des actions correctes et raisonnables. Un véhicule doté de capacités de conduite autonome est généralement équipé de différents types de capteurs de collecte d'informations, tels que des capteurs de caméra à vision panoramique, des capteurs lidar, des capteurs radar à ondes millimétriques, etc., pour garantir que le véhicule autonome peut percevoir et comprendre avec précision l'environnement environnant. éléments , permettant aux véhicules autonomes de prendre les bonnes décisions pendant la conduite autonome. Tête





