Comment utiliser l'algorithme de Dijkstra pour trouver l'itinéraire le plus économique pour le 1er mai

Demain, c'est le 1er mai, êtes-vous prêt pour votre guide de voyage ? Aujourd'hui, l'éditeur vous présentera un article sur l'utilisation de l'algorithme dijkstra pour vous aider à trouver facilement des itinéraires de voyage, à un prix abordable et sans souci. Venez jeter un œil !

Cas :

Le 1er mai approche bientôt et Xiao Zhang est prêt à voyager !

J'ai vérifié les billets d'avion de divers endroits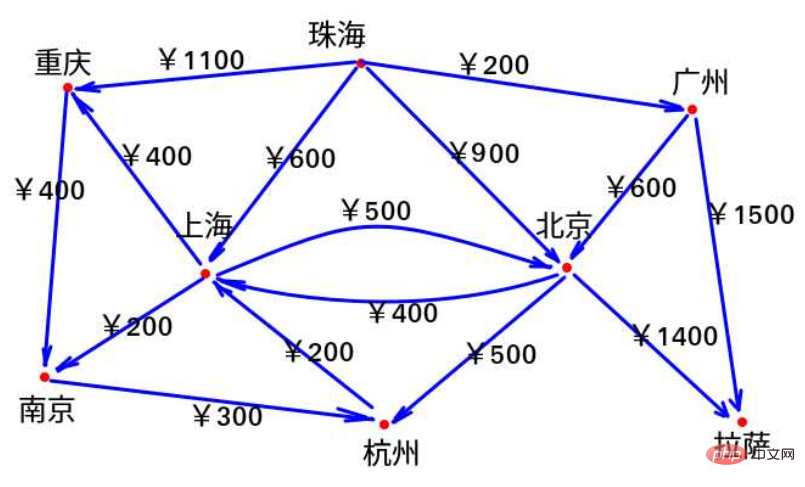

　
Parce que mon salaire a été très mal déduit cette année, Xiao Zhang n'a pas beaucoup d'argent et doit faire attention à son budget. Il veut connaître le coût le plus bas pour se rendre dans différentes villes.
【Eh bien, il n'est pas nécessaire de considérer le coût du retour. Xiao Zhang allait dire à l'oncle de la police qu'il avait été enlevé et qu'il serait renvoyé gratuitement. 】
S'il veut voler de Zhuhai à Lhassa, quel est le coût minimum du billet ? Parlons de l'algorithme dont nous allons parler aujourd'hui.

Algorithme de Dijkstra

L'algorithme de Dijkstra est un algorithme de chemin le plus court à source unique typique, utilisé pour calculer le chemin le plus court d'un nœud à tous les autres nœuds. La principale caractéristique est qu'il s'étend vers l'extérieur couche par couche depuis le point de départ jusqu'à ce qu'il atteigne le point final. La complexité temporelle de l'algorithme de Dijkstra est O(N^2).

Extension

Dijkstra est née le 11 mai 1930 dans une famille intellectuelle de Rotterdam, aux Pays-Bas. Elle était la troisième de quatre frères et sœurs. Son père était un chimiste et inventeur qui a été président de la Dutch Chemical Society. Sa mère est mathématicienne. Il a conçu et mis en œuvre avec succès un algorithme efficace pour trouver le chemin le plus court entre deux emplacements comportant des obstacles. Cet algorithme a été nommé « algorithme de Dijkstra » et a résolu un problème très critique en robotique. Le problème, à savoir le problème de planification de la trajectoire de mouvement, est encore largement utilisé. aujourd'hui.

Tutoriels associés : Images de l'aventure de la structure des données

Dérivation d'algorithme

Créer un tableau pour enregistrer Zhuhai The coût minimum du billet d'avion pour chaque ville

Nous avons commencé à rechercher des villes directement connectées depuis Zhuhai

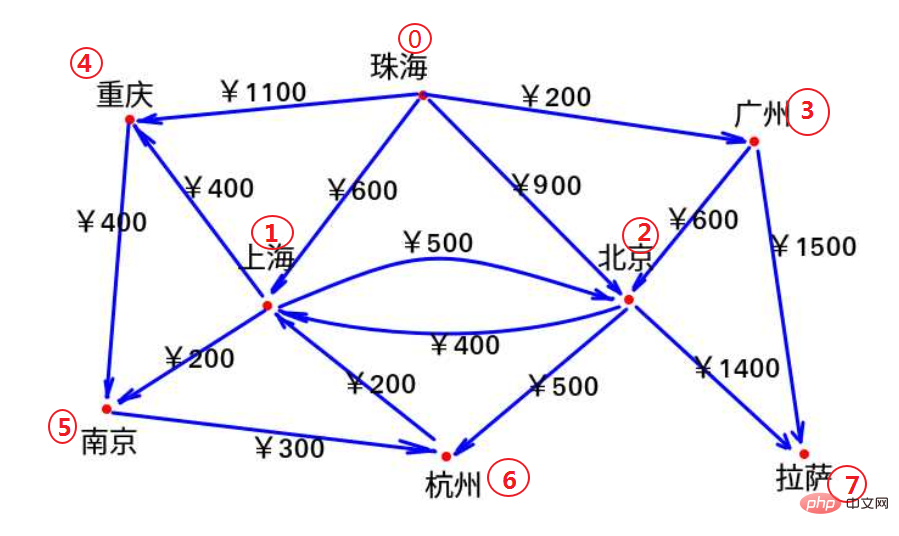
Les villes directement connectées à Zhuhai comprennent Shanghai, Pékin, Guangzhou et Chongqing, puis Les prix des billets d'avion de Zhuhai vers d'autres villes sont les suivants (s'il n'y a pas de connexion directe, on marque l'infini) :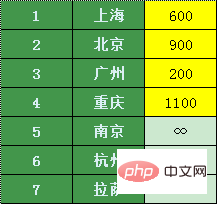

On constate que parmi ces quatre villes, Guangzhou a la prix le plus bas, alors transférons depuis Guangzhou

Transfert depuis Guangzhou, qui propose les billets d'avion les moins chers

Les villes qui peuvent être directement reliées à Guangzhou sont Pékin et Lhassa. Ensuite, les prix des billets pour la correspondance. les vols de Zhuhai vers d'autres villes de Guangzhou sont les suivants : (Il est impossible de savoir si vous pouvez transférer depuis Guangzhou)

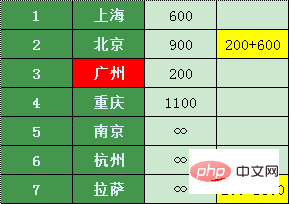
La comparaison a révélé qu'il s'agit de 200 yuans de Zhuhai à Guangzhou et de 600 yuans de Guangzhou à Pékin, ce qui ne coûte que 800 yuans (c'est peut-être une perte de temps, mais peu importe, Xiao Zhang est pauvre et n'a plus que du temps)
C'est 1700 de Guangzhou à Lhassa, donc ce n'est certainement pas mieux que y arriver.
Après ce calcul, nous avons la liste de prix la moins chère.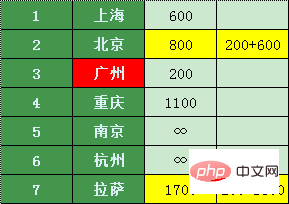

En plus de Guangzhou, cherchons la ville la moins chère pour transférer des vols depuis - Shanghai

Chongqing et Nanjing sont des villes directement reliées à Shanghai, puis Zhuhai se connecte à d'autres villes depuis Shanghai Les prix des billets d'avion dans les villes sont les suivants :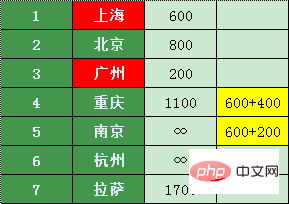

En comparant les prix d'origine, nous avons constaté qu'il est moins cher de transférer de Shanghai à Chongqing et Nanjing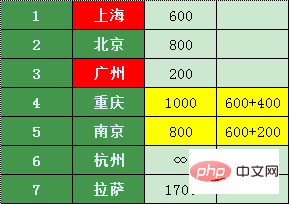

Sauf Guangzhou et Shanghai, alors cherchons la ville la moins chère pour les vols de correspondance - Pékin

Pékin est direct vers Shanghai (Shanghai a été marqué, ce doit être le prix le moins cher, en en fait, cela n'a aucun sens de comparer), Hangzhou et Lhassa, les prix comme suit :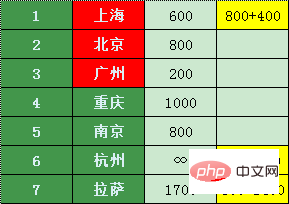

Le prix pour Lhassa est le prix le plus bas pour Pékin 800 + Pékin-> les prix de 1400 à Lhassa (2200) sont supérieurs à 1700, et 800 + 500 = 1300 à Hangzhou, alors la liste de prix minimum est la suivante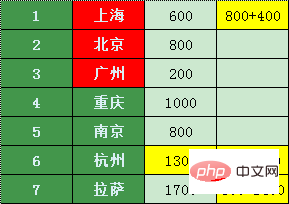

En plus de Guangzhou, Shanghai et Pékin, trouvons la ville la moins chère pour transférer les vols depuis - Nanjing

Nanjing ne peut aller directement qu'à Hangzhou,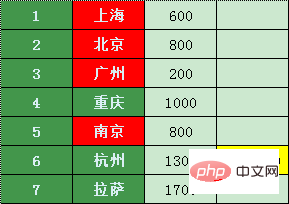

Le prix à partir de Nanjing à Hangzhou Il est 11h00, ce qui est une bonne affaire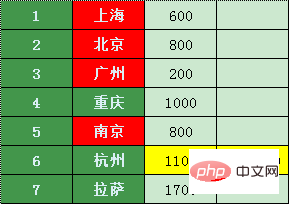

En plus de Guangzhou, Shanghai, Pékin et Nanjing, cherchons la ville la moins chère pour les vols de correspondance - Chongqing

La seule connexion directe depuis Chongqing est Nanjing, et il en coûte 1 000 + 400 = 1 400 yuans pour aller à Nanjing, ce qui n'est certainement pas rentable par rapport aux 800 yuans d'origine pour Nanjing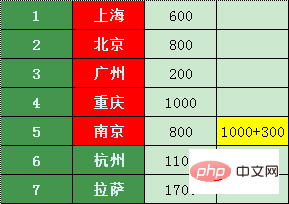

Sauf Guangzhou, Shanghai, Pékin, Nanjing et Chongqing, puis depuis Cherchons la ville avec le transfert le moins cher - Hangzhou

Hangzhou ne peut aller qu'à Shanghai, et le prix est plus élevé que Shanghai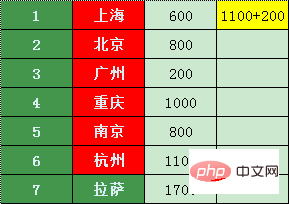

Enfin nous avons trouvé Lhassa

Ensuite, le billet d'avion le moins cher pour Lhassa est de 1 700 yuans.

Mise en œuvre du code

Préparation des variables

1) Utilisez 0, 1, 2, , 7 pour représenter Zhuhai, Shanghai, Pékin, Guangzhou, Chongqing, Nanjing,. respectivement Hangzhou, Lhassa.
2) Utilisez un tableau bidimensionnel de prix [8][8] pour représenter les prix des vols : prix[i][j] = prix du vol direct de i à j (s'il n'y a pas de vol, il est enregistré comme ∞ )
3) Utilisez un tableau minPrice pour enregistrer le coût minimum du billet d'avion de Zhuhai à chaque ville :
4) Utilisez un tableau de drapeaux pour marquer si la ville a été transférée

    //    表示无穷大 即不可达
    public static int NO_AIRPLANE = Integer.MAX_VALUE;
//    初始直飞价格表
    public int[][]  prices ;
    //    最优转机价格表
    public int[]   minPrice ;
    public boolean[] flag ;
    private int citySize;

Préparation des données

 public static int[][] getPrices(){
        int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS  = 7;
        int[][] prices =  new int[8][8];
        //from Zhuhai
        prices[ZH][CQ] = 1100;
        prices[ZH][SH] = 600;
        prices[ZH][BJ] = 900;
        prices[ZH][GZ] = 200;
        //others
        prices[CQ][NJ] = 400;
        prices[SH][CQ] = 400;
        prices[SH][BJ] = 500;
        prices[SH][NJ] = 200;
        prices[BJ][SH] = 400;
        prices[BJ][HZ] = 500 ;
        prices[BJ][LS] = 1400;
        prices[GZ][BJ] = 600 ;
        prices[GZ][LS] = 1500 ;
        prices[NJ][HZ] = 300 ;
        prices[HZ][SH] = 200 ;
        for(int i = 0 ; i < 8 ; i++){
            for(int j = 0 ; j < 8 ; j++){
                if(prices[i][j] == 0){
                    prices[i][j] =  NO_AIRPLANE;
                }
            }
        }
        return prices;
    }

Initialiser le vol direct Hangzhou Le prix

//            初始化始发站价格表
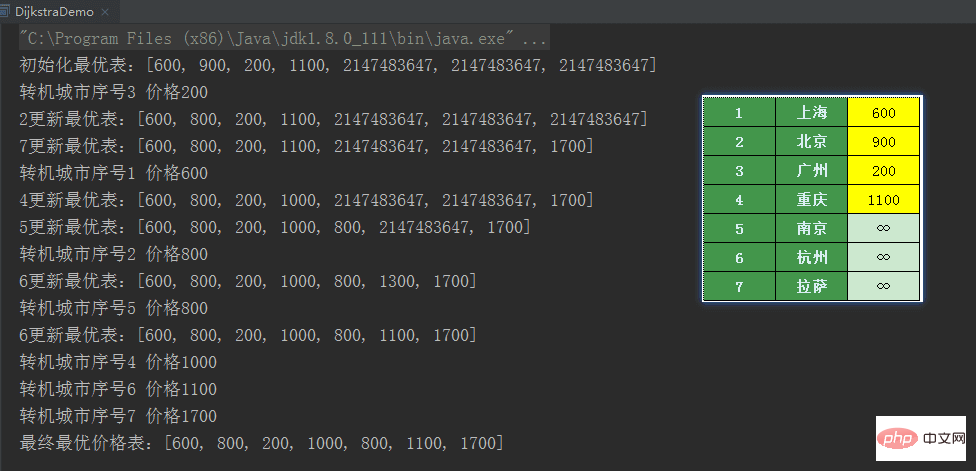
        for(int i = 1; i < citySize;i++){
            minPrice[i-1] = prices[0][i];
        }

implémentation de l'algorithme

private void dijkstra(){
        int min = Integer.MAX_VALUE;
        int minIdx = Integer.MAX_VALUE;
//        找到最小的价格
        for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
            if(!flag[idx] &&  minPrice[idx] < min ){
                min = minPrice[idx];
                minIdx =  idx ;
            }
        }
        if(minIdx == Integer.MAX_VALUE){
//            已经没有最小的了
            return ;
        }
        //标记从该城市转机
        flag[minIdx] = true;
        minIdx += 1;
        System.out.println("最小城市序号"+minIdx +" 价格"+ minPrice[minIdx -1]);
 //        获取当前城市的价格表
        int cityPrice =  minPrice[minIdx -1];
        int[] minCityPrices = prices[minIdx];
        for(int idx = 1 ; idx < citySize ; idx ++ ){
            int price = minCityPrices[idx];
//            如果从杭州到达该城市的价格 加上 idx城市转机的价格 低于  从杭州到达idx城市的价格 则更新
            if(!flag[idx -1 ] && price != NO_AIRPLANE  && (cityPrice+ price) < minPrice[idx - 1]){
//            可达的城市到达的
                minPrice[idx - 1] = cityPrice+ price;
                System.out.println(idx+"更新最优表：" + Arrays.toString(minPrice));
            }
        }
        dijkstra();
    }

Le résultat en cours

est cohérent avec la poussée ci-dessus processus. J’espère que cet article pourra vous aider.

Code source de la pièce jointe :

package a;
 
import java.util.Arrays;
 
/**
 * 　　　　　　　　┏┓　　　┏┓+ +
 * 　　　　　　　┏┛┻━━━┛┻┓ + +
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┃　　　━　　　┃ ++ + + +
 * 　　　　　　 ████━████ ┃+
 * 　　　　　　　┃　　　　　　　┃ +
 * 　　　　　　　┃　　　┻　　　┃
 * 　　　　　　　┃　　　　　　　┃ + +
 * 　　　　　　　┗━┓　　　┏━┛
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃ + + + +
 * 　　　　　　　　　┃　　　┃　　　　Code is far away from bug with the animal protecting
 * 　　　　　　　　　┃　　　┃ + 　　　　神兽保佑,代码无bug
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃　　+
 * 　　　　　　　　　┃　 　　┗━━━┓ + +
 * 　　　　　　　　　┃ 　　　　　　　┣┓
 * 　　　　　　　　　┃ 　　　　　　　┏┛
 * 　　　　　　　　　┗┓┓┏━┳┓┏┛ + + + +
 * 　　　　　　　　　　┃┫┫　┃┫┫
 * 　　　　　　　　　　┗┻┛　┗┻┛+ + + +
 *
 * @Author:Halburt
 * @Date:2019-04-24 下午 5:47
 * @Description:
 */
public class DijkstraDemo {
 
    //    表示无穷大 即不可达
    public static int NO_AIRPLANE = Integer.MAX_VALUE;
//    初始直飞价格表
    public int[][]  prices ;
    //    最优转机价格表
    public int[]   minPrice ;
    public boolean[] flag ;
    private int citySize;
    /**
     * @param citySize 城市数量
     */
    public DijkstraDemo(int citySize){
        this.citySize = citySize;
//      prices = new int [citySize][citySize];
        flag  =  new boolean [citySize - 1];
        minPrice = new int[citySize - 1 ];
    }
    public static int[][] getPrices(){
        int ZH = 0,SH = 1, BJ = 2, GZ = 3,CQ = 4,NJ = 5, HZ = 6,LS  = 7;
        int[][] prices =  new int[8][8];
        //from Zhuhai
        prices[ZH][CQ] = 1100;
        prices[ZH][SH] = 600;
        prices[ZH][BJ] = 900;
        prices[ZH][GZ] = 200;
        //others
        prices[CQ][NJ] = 400;
        prices[SH][CQ] = 400;
        prices[SH][BJ] = 500;
        prices[SH][NJ] = 200;
        prices[BJ][SH] = 400;
        prices[BJ][HZ] = 500 ;
        prices[BJ][LS] = 1400;
        prices[GZ][BJ] = 600 ;
        prices[GZ][LS] = 1500 ;
        prices[NJ][HZ] = 300 ;
        prices[HZ][SH] = 200 ;
        for(int i = 0 ; i < 8 ; i++){
            for(int j = 0 ; j < 8 ; j++){
                if(prices[i][j] == 0){
                    prices[i][j] =  NO_AIRPLANE;
                }
            }
        }
        return prices;
    }
    public static void main(String[] args) {
        DijkstraDemo demo = new DijkstraDemo(8);
        demo.dijkstra(getPrices());
    }
 
    public void dijkstra(int[][]  prices ){
        this.prices = prices;
//        初始化
//            初始化始发站价格表
        for(int i = 1; i < citySize;i++){
            minPrice[i-1] = prices[0][i];
        }
        System.out.println("初始化最优表：" + Arrays.toString(minPrice));
        dijkstra();
        System.out.println("最终最优价格表：" + Arrays.toString(minPrice));
    }
 
    private void dijkstra(){
        int min = Integer.MAX_VALUE;
        int minIdx = Integer.MAX_VALUE;
//        找到最小的价格
        for(int idx = 0 ; idx < minPrice.length ; idx ++ ) {
            if(!flag[idx] &&  minPrice[idx] < min ){
                min = minPrice[idx];
                minIdx =  idx ;
            }
        }//=已经没有最小的了
        if(minIdx == Integer.MAX_VALUE){
            return ;
        }
        //标记从该城市转机
        flag[minIdx] = true;
        minIdx += 1;
        System.out.println("转机城市序号"+minIdx +" 价格"+ minPrice[minIdx -1]);
       //获取该城市转机时飞往其他城市的价格表
        int cityPrice =  minPrice[minIdx -1];
        //获取杭州飞往该城市的价格
        int[] minCityPrices = prices[minIdx];
        for(int idx = 1 ; idx < citySize ; idx ++ ){
            int price = minCityPrices[idx];
//            如果从杭州到达该城市的价格 加上 idx城市转机的价格 低于  从杭州到达idx城市的价格 则更新
            if(!flag[idx -1 ] && price != NO_AIRPLANE  && (cityPrice+ price) < minPrice[idx - 1]){
//            可达的城市到达的
                minPrice[idx - 1] = cityPrice+ price;
                System.out.println(idx+"更新最优表：" + Arrays.toString(minPrice));
            }
        }
        dijkstra();
    }
 
 
 

 
}

Merci à l'auteur original Halburt, adresse originale : https://www.cnblogs.com/Halburt/p/10767389.html

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!