algorithme de recherche binaire

La recherche binaire est également appelée recherche binaire, qui est une méthode de recherche plus efficace. Cependant, la recherche binaire nécessite que le tableau linéaire adopte une structure de stockage séquentielle et que les éléments du tableau soient classés par mots-clés.

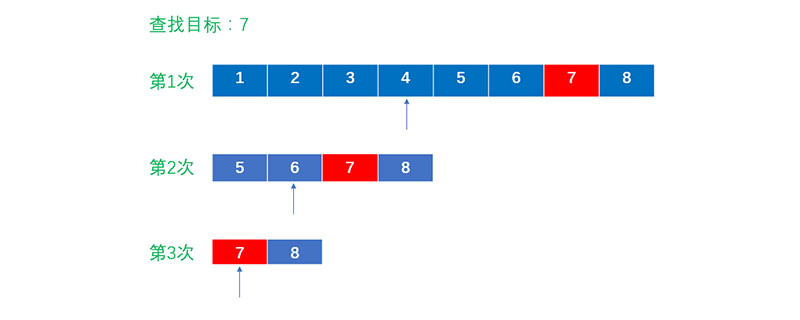
Processus de recherche

Tout d'abord, en supposant que les éléments du tableau sont classés par ordre croissant, enregistrez la clé au milieu du tableau Le mot est comparé au mot-clé de recherche. Si les deux sont égaux, la recherche est réussie ; sinon, l'enregistrement de la position médiane est utilisé pour diviser le tableau en premier et dernier sous-tableaux. enregistré en position médiane est supérieur au mot-clé de recherche, la recherche se poursuit dans le sous-tableau précédent, sinon la recherche se poursuit pour le sous-tableau suivant. Répétez le processus ci-dessus jusqu'à ce qu'un enregistrement répondant aux conditions soit trouvé, ce qui rend la recherche réussie, ou jusqu'à ce que la sous-table n'existe plus, auquel cas la recherche échoue.

Nombre de comparaisons

Formule de calcul :

Lorsque la table de séquence comporte n mots-clés :

Lorsque la recherche échoue, comparez le mot-clé au moins une fois ; lorsque la recherche réussit, le nombre maximum de comparaisons de mots-clés est de b.

Remarque : a, b, n sont tous des entiers positifs.

Complexité de l'algorithme

L'idée de base de la recherche binaire est de diviser n éléments en deux parties à peu près égales et de comparer a[n/2] avec x, Si x=a[n/2], alors x est trouvé et l'algorithme se termine si x

La complexité temporelle n'est rien de plus que le nombre de boucles while !

Il y a n éléments au total,

suit progressivement n, n/2, n/4,....n/2^k (le nombre d'éléments restant sera exploité ensuite ), où k est le nombre de cycles

Puisque votre n/2^k est arrondi >=1

c'est-à-dire n/2^k=1

peut être obtenu k=log2n, (c'est le logarithme de n en base 2)

Donc la complexité temporelle peut être exprimée comme O(h)=O(log2n)

Une bissection est fournie ci-dessous. Trouvez le pseudocode de l'implémentation :

BinarySearch(max,min,des)

mid-<(max+min)/2

while(min< =max)

mid=(min+max)/2

si mid=des alors

revenir milieu

sinon mid >des then

max=mid-1

else

min=mid+1

return max

Demi recherche La méthode est également appelée recherche binaire. Cette méthode utilise pleinement la relation d'ordre entre les éléments et adopte la stratégie diviser pour régner, qui peut terminer la tâche de recherche en O(log n) dans le pire des cas. Son idée de base est la suivante : (en supposant que les éléments du tableau sont classés par ordre croissant) divisez n éléments en deux moitiés avec à peu près le même nombre, prenez a[n/2] et comparez-le avec le x que vous voulez trouver, si x= a[n/ 2] alors x est trouvé et l'algorithme se termine ; si x

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!