Algorithmes en python

Définition de l'algorithme
Un algorithme (algorithme) fait référence à une description précise et complète d'une solution de résolution de problèmes et est une série de instructions claires pour résoudre les problèmes. Les algorithmes représentent une approche systématique pour décrire le mécanisme stratégique de résolution des problèmes. En d’autres termes, il est possible d’obtenir le résultat requis dans un temps limité pour certains intrants standardisés. Si un algorithme est défectueux ou inapproprié pour résoudre un problème, son exécution ne résoudra pas le problème. Différents algorithmes peuvent utiliser différents temps, espace ou efficacité pour accomplir la même tâche. La qualité d’un algorithme peut être mesurée par sa complexité spatiale et sa complexité temporelle.
Un algorithme doit avoir les sept caractéristiques importantes suivantes :
①Finitité : La finitude d'un algorithme signifie que l'algorithme doit pouvoir se terminer après l'exécution d'un nombre limité d'étapes ; 🎜>②Défini : Chaque étape de l'algorithme doit avoir une définition exacte ;
③Entrée : Un algorithme a 0 ou plusieurs entrées pour décrire l'opérande La situation initiale, l'entrée dite 0 fait référence aux conditions initiales définies. par l'algorithme lui-même ;
④Sortie : Un algorithme a une ou plusieurs sorties pour refléter les résultats du traitement des données d'entrée . Un algorithme sans sortie n'a aucun sens ;
⑤Efficacité : toute étape de calcul effectuée dans l'algorithme peut être décomposée en étapes d'opération de base exécutables, c'est-à-dire que chaque étape de calcul peut toutes être complétée dans un temps limité (également appelé efficacité) ;
⑥Haute efficacité : exécution rapide et faible utilisation des ressources
⑦Robustness (Robustness) : Réponse correcte aux données.
Complexité temporelle
En informatique, la complexité temporelle d'un algorithme est une fonction qui décrit quantitativement le temps d'exécution et la complexité temporelle de l'algorithme. La notation Big O utilisée (notation Big O) est une notation mathématique utilisée pour décrire le comportement asymptotique d'une fonction. Plus précisément, il s'agit d'une fonction qui utilise une autre fonction (généralement plus simple) pour décrire la limite supérieure asymptotique de l'ordre de grandeur de. une fonction. Lié. En mathématiques, il est généralement utilisé pour décrire le reste d'une série infinie tronquée, notamment une série asymptotique ; en informatique, il est très utile pour analyser la complexité des algorithmes, en utilisant cette méthode. la complexité peut être considérée comme asymptotique, ce qui considère la situation dans laquelle la taille de la valeur d'entrée approche l'infini.
Big O, en bref, cela peut être considéré comme signifiant « ordre de » (environ).
Asymptotique infinie
La notation Big O est très utile pour analyser l'efficacité d'un algorithme. Par exemple, le temps nécessaire pour résoudre un problème de taille n (ou le nombre d'étapes nécessaires) peut être trouvé : T(n) = 4n^2 - 2n + 2.À mesure que n augmente, le terme n^2 ; commencera à dominer, et les autres termes peuvent être ignorés - par exemple : lorsque n = 500, le terme 4n^2 est 1000 fois plus grand que le terme 2n, donc , dans la plupart des cas, l'effet de l'omission de ce dernier sur la valeur de l'expression sera négligeable.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer : superviser explicitement la structure BEVFormer pour améliorer les performances de détection à longue traîne
Mar 26, 2024 pm 12:41 PM
Écrit ci-dessus et compréhension personnelle de l'auteur : À l'heure actuelle, dans l'ensemble du système de conduite autonome, le module de perception joue un rôle essentiel. Le véhicule autonome roulant sur la route ne peut obtenir des résultats de perception précis que via le module de perception en aval. dans le système de conduite autonome, prend des jugements et des décisions comportementales opportuns et corrects. Actuellement, les voitures dotées de fonctions de conduite autonome sont généralement équipées d'une variété de capteurs d'informations de données, notamment des capteurs de caméra à vision panoramique, des capteurs lidar et des capteurs radar à ondes millimétriques pour collecter des informations selon différentes modalités afin d'accomplir des tâches de perception précises. L'algorithme de perception BEV basé sur la vision pure est privilégié par l'industrie en raison de son faible coût matériel et de sa facilité de déploiement, et ses résultats peuvent être facilement appliqués à diverses tâches en aval.
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
Explorez les principes sous-jacents et la sélection d'algorithmes de la fonction de tri C++
Apr 02, 2024 pm 05:36 PM
La couche inférieure de la fonction de tri C++ utilise le tri par fusion, sa complexité est O(nlogn) et propose différents choix d'algorithmes de tri, notamment le tri rapide, le tri par tas et le tri stable.
 L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
L'intelligence artificielle peut-elle prédire la criminalité ? Explorez les capacités de CrimeGPT
Mar 22, 2024 pm 10:10 PM
La convergence de l’intelligence artificielle (IA) et des forces de l’ordre ouvre de nouvelles possibilités en matière de prévention et de détection de la criminalité. Les capacités prédictives de l’intelligence artificielle sont largement utilisées dans des systèmes tels que CrimeGPT (Crime Prediction Technology) pour prédire les activités criminelles. Cet article explore le potentiel de l’intelligence artificielle dans la prédiction de la criminalité, ses applications actuelles, les défis auxquels elle est confrontée et les éventuelles implications éthiques de cette technologie. Intelligence artificielle et prédiction de la criminalité : les bases CrimeGPT utilise des algorithmes d'apprentissage automatique pour analyser de grands ensembles de données, identifiant des modèles qui peuvent prédire où et quand les crimes sont susceptibles de se produire. Ces ensembles de données comprennent des statistiques historiques sur la criminalité, des informations démographiques, des indicateurs économiques, des tendances météorologiques, etc. En identifiant les tendances qui pourraient échapper aux analystes humains, l'intelligence artificielle peut donner du pouvoir aux forces de l'ordre.
 Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
Algorithme de détection amélioré : pour la détection de cibles dans des images de télédétection optique haute résolution
Jun 06, 2024 pm 12:33 PM
01Aperçu des perspectives Actuellement, il est difficile d'atteindre un équilibre approprié entre efficacité de détection et résultats de détection. Nous avons développé un algorithme YOLOv5 amélioré pour la détection de cibles dans des images de télédétection optique haute résolution, en utilisant des pyramides de caractéristiques multicouches, des stratégies de têtes de détection multiples et des modules d'attention hybrides pour améliorer l'effet du réseau de détection de cibles dans les images de télédétection optique. Selon l'ensemble de données SIMD, le mAP du nouvel algorithme est 2,2 % meilleur que YOLOv5 et 8,48 % meilleur que YOLOX, permettant ainsi d'obtenir un meilleur équilibre entre les résultats de détection et la vitesse. 02 Contexte et motivation Avec le développement rapide de la technologie de télédétection, les images de télédétection optique à haute résolution ont été utilisées pour décrire de nombreux objets à la surface de la Terre, notamment des avions, des voitures, des bâtiments, etc. Détection d'objets dans l'interprétation d'images de télédétection
 Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
Pratique et réflexion sur la plateforme multimodale de grands modèles Jiuzhang Yunji DataCanvas
Oct 20, 2023 am 08:45 AM
1. Le développement historique des grands modèles multimodaux. La photo ci-dessus est le premier atelier sur l'intelligence artificielle organisé au Dartmouth College aux États-Unis en 1956. Cette conférence est également considérée comme le coup d'envoi du développement de l'intelligence artificielle. pionniers de la logique symbolique (à l'exception du neurobiologiste Peter Milner au milieu du premier rang). Cependant, cette théorie de la logique symbolique n’a pas pu être réalisée avant longtemps et a même marqué le début du premier hiver de l’IA dans les années 1980 et 1990. Il a fallu attendre la récente mise en œuvre de grands modèles de langage pour découvrir que les réseaux de neurones portent réellement cette pensée logique. Les travaux du neurobiologiste Peter Milner ont inspiré le développement ultérieur des réseaux de neurones artificiels, et c'est pour cette raison qu'il a été invité à y participer. dans ce projet.
 Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
Application d'algorithmes dans la construction de 58 plateformes de portraits
May 09, 2024 am 09:01 AM
1. Contexte de la construction de la plateforme 58 Portraits Tout d'abord, je voudrais partager avec vous le contexte de la construction de la plateforme 58 Portraits. 1. La pensée traditionnelle de la plate-forme de profilage traditionnelle ne suffit plus. La création d'une plate-forme de profilage des utilisateurs s'appuie sur des capacités de modélisation d'entrepôt de données pour intégrer les données de plusieurs secteurs d'activité afin de créer des portraits d'utilisateurs précis. Elle nécessite également l'exploration de données pour comprendre le comportement et les intérêts des utilisateurs. et besoins, et fournir des capacités côté algorithmes ; enfin, il doit également disposer de capacités de plate-forme de données pour stocker, interroger et partager efficacement les données de profil utilisateur et fournir des services de profil. La principale différence entre une plate-forme de profilage d'entreprise auto-construite et une plate-forme de profilage de middle-office est que la plate-forme de profilage auto-construite dessert un seul secteur d'activité et peut être personnalisée à la demande. La plate-forme de mid-office dessert plusieurs secteurs d'activité et est complexe ; modélisation et offre des fonctionnalités plus générales. 2.58 Portraits d'utilisateurs de l'arrière-plan de la construction du portrait sur la plate-forme médiane 58
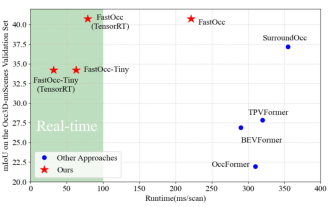 Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Ajoutez SOTA en temps réel et montez en flèche ! FastOcc : un algorithme Occ plus rapide et convivial pour le déploiement est là !
Mar 14, 2024 pm 11:50 PM
Écrit ci-dessus & La compréhension personnelle de l'auteur est que dans le système de conduite autonome, la tâche de perception est un élément crucial de l'ensemble du système de conduite autonome. L'objectif principal de la tâche de perception est de permettre aux véhicules autonomes de comprendre et de percevoir les éléments environnementaux environnants, tels que les véhicules circulant sur la route, les piétons au bord de la route, les obstacles rencontrés lors de la conduite, les panneaux de signalisation sur la route, etc., aidant ainsi en aval modules Prendre des décisions et des actions correctes et raisonnables. Un véhicule doté de capacités de conduite autonome est généralement équipé de différents types de capteurs de collecte d'informations, tels que des capteurs de caméra à vision panoramique, des capteurs lidar, des capteurs radar à ondes millimétriques, etc., pour garantir que le véhicule autonome peut percevoir et comprendre avec précision l'environnement environnant. éléments , permettant aux véhicules autonomes de prendre les bonnes décisions pendant la conduite autonome. Tête






