sélection de temps linéaire

Définition : Étant donné n éléments dans une séquence linéaire et un entier k, 1≤k≤n, il faut trouver le kième plus petit parmi ces n éléments éléments.

(1) Dans certains cas particuliers, il est facile de concevoir un algorithme de temps linéaire pour résoudre le problème de sélection. Par exemple : lorsque l'on souhaite sélectionner le plus grand élément ou le plus petit élément, cela peut évidemment se faire en un temps O(n). (Juste une comparaison)

(2) Le problème général de sélection, notamment le problème de sélection de la médiane, semble être plus difficile que le plus petit (grand) élément. Mais en fait, dans un ordre asymptotique, ce sont les mêmes. Cela peut également être fait en temps O(n).

Première méthode de sélection temporelle linéaire : randomizedSelect

Idée : Adapter le tri rapide aléatoire, au lieu de trier l'ensemble du tableau, mais le tri sélectionné ( Plus rapide)

Complexité temporelle :

(1) Dans le pire des cas, l'algorithme randomizedSelect nécessite un temps de calcul O(n^2)

par exemple . Nous devons trouver le plus petit élément, mais la position obtenue à chaque fois que nous divisons par la fonction Partition est toujours très grande (proche de n) (c'est-à-dire qu'elle est toujours divisée au niveau du plus grand élément)

( 2) Mais c'est possible. Il est prouvé que l'algorithme randomizedSelect peut trouver le kième plus petit élément parmi n éléments d'entrée en un temps moyen O(n).

Le code est le suivant :

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

int Partition(int a[],int p,int r){
    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int RandomizedPartition(int a[],int p,int r){
    int i=rand()%(r-p)+p;
    swap(a[p],a[i]);
    return Partition(a,p,r);
}

int RandomizedSelect(int a[],int p,int r,int k){
    if(p==r)return a[p];
    int i=RandomizedPartition(a,p,r);//返回基准元素的位置
    int j=i-p+1;//表示基准元素及其左边一共多少个元素
    if(k<=j)RandomizedSelect(a,p,i,k);
    else RandomizedSelect(a,i+1,r,k-j);
}
int main(){
    int a[10]={3,1,7,6,5,9,8,2,0,4};
    int x;
    while(scanf("%d",&x)!=EOF){
        int ans=RandomizedSelect(a,0,9,x);
        printf("%d\n",ans);
    }
}

Méthode de sélection du temps linéaire deux :

Si vous pouvez trouver a<🎜 en temps linéaire >Base de division, de sorte que la longueur des deux sous-tableaux divisés selon cette base soit au moins ε fois la longueur du tableau d'origine (0<ε<1 est une certaine constante positive), alors il peut être utilisé dans le pire des cas. Il faut un temps O(n) pour terminer la tâche de sélection.

Par exemple, si ε=9/10, la longueur du sous-tableau généré par l'appel récursif de l'algorithme est raccourcie d'au moins 1/10. Ainsi, dans le pire des cas, le temps de calcul T(n) requis par l'algorithme satisfait la formule récursive T(n)≤T(9n/10)+O(n). De là, nous pouvons obtenir T(n)=O(n).

Lorsque le professeur en a parlé, je m'en souviens très clairement. Il a souligné que

trouver plutôt que déterminer signifie trouver la médiane. nous voulons.La valeur, et notre tri rapide précédent, etc., visaient à déterminer la position de la valeur, c'est-à-dire à placer l'élément de référence dans la position correcte.

Étapes :

(1) Divisez n éléments d'entrée en n/5 groupes (arrondis), chacun Le groupe contient 5 éléments, et il peut y avoir au plus un groupe qui ne contient pas 5 éléments. Utilisez n'importe quel algorithme de tri pour trier les éléments de chaque groupe et prenez la médiane de chaque groupe, un total de n/5 (arrondi au supérieur).

(2) Appelez récursivement select pour trouver la médiane de ces n/5 (arrondis) éléments. Si n/5 (arrondi au supérieur) est un nombre pair, trouvez la plus grande de ses 2 médianes. Utilisez cet élément comme base de division.

Schéma de principe de la stratégie de partitionnement :

Point blanc : médiane de chaque groupe ; Point x : médiane de la médiane

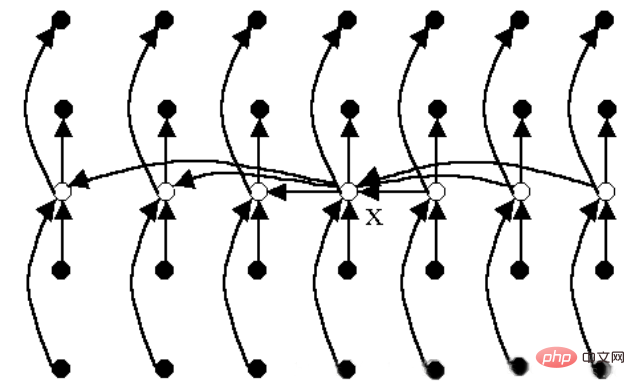
Exemple :

Par ordre croissant, trouvez ce qui suit Le 18ème élément sur 29 éléments : 8,31,60,33,17,4,51,57,49,35,11,43,37,3,13,52,6,19,25,32,

54,16,5,41,7,23,22,46,29.
(1) Divisez les 25 premiers éléments en 5 (=floor(29/5)) groupes : (8,31,60, 33 ,17),(4,51,57,49,35),(11,43,37,3,13),(52,6,19,25,32),(54,16,5,41, 7 );
(2) Extraire l'élément médian de chaque groupe pour former l'ensemble {31,49,13,25,16};
(3) Utiliser récursivement l'algorithme pour trouver la médiane de l'ensemble, Obtenir m=25;
(4) D'après m=25, divisez les 29 éléments en 3 sous-tableaux (dans l'ordre d'origine)
P={8,17,4,11, 3,13,6 ,19 ,16,5,7,23,22}
Q={25}

R={31,60,33,51,57,49,35,43,37,52, 32, 54,41,46,29}

(5) Puisque |P|=13,|Q|=1,k=18, alors abandonnez P et Q et faites k=18-13-1 = 4, exécutez cet algorithme de manière récursive sur R ;

(6) Divisez R en 3 (floor(15/5)) groupes : {31,60,33,51,57},{49,35,43 ,37, 52},{32,54,41,46,29}
(7) Trouver l'élément médian de ces trois groupes d'éléments : {51,43,41}, l'élément médian de cet ensemble est 43 ;
(8) Divisez R en 3 groupes basés sur 43 :

{31, 33, 35,37,32, 41, 29},{43},{60, 51,57, 49, 52, 54, 46}

Complexité :

Supposons que la longueur du tableau soit n

Lorsque n<75, le temps de calcul utilisé par l'algorithme sélectionne Ne dépassant pas un certain constante C1
Quand n≥75, la boucle for est exécutée n/5 fois, et à chaque fois elle prend une certaine constante (un nombre fixe est à chercher parmi 5 !) ; la longueur est 1/5 de la longueur d'origine, le temps pris peut être enregistré sous la forme T(n/5) ; après division, le tableau obtenu comporte au plus 3n/4 éléments et le temps pris est enregistré sous la forme T(3n/4) ; ). Ainsi T(n) peut être exprimé récursivement comme :

La solution de cette expression récursive est T(n)=O(n)

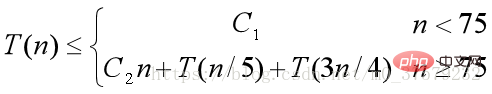
上述算法将每一组的大小定为5，并选取75作为是否作递归调用的分界点（大于75使用该算法）。这2点保证了T(n)的递归式中2个自变量之和n/5+3n/4=19n/20=εn，0<ε<1。这是使T(n)=O(n)的关键之处。当然，除了5和75之外，还有其他选择。

注意：

（1）设中位数的中位数是x，比x小和比x大的元素至少3*(n-5)/10个，原因：

3*(n/5-1)*1/2

3---中位数比x小的每一组中有3个元素比x小

n/5-1---有5个数的组数

1/2---大概有1/2组的中位数比x小

（2）而当n≥75时，3(n-5)/10≥n/4所以按此基准划分所得的2个子数组的长度都至少缩短1/4，也就是说，长度最长为原长度的3/4。

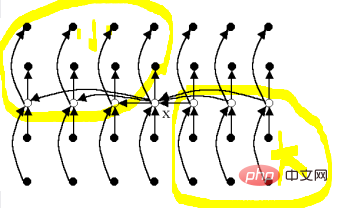
如图，划分的部分左上是肯定比x小的（大概占1/4）右下是肯定比x大的（大概占1/4）左下和右上不确定，就算这两部分同时不比x小或比x大，划分成的子区间也能至少缩短1/4!

核心代码：

Type Select(Type a[], int p, int r, int k)
{
      if (r-p<75) {
        //用某个简单排序算法对数组a[p:r]排序;
        return a[p+k-1];
        };
      for (int i=0;i<=(r-p-4)/5;i++)//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面
  
      //找中位数的中位数，r-p-4即上面所说的n-5
      Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//x是中位数的中位数
      int i=Partition(a,p,r,x),j=i-p+1;//i为快排一趟找到区间[p,r]中x应该在的位置，j为[p,i]区间的元素个数
      if (k<=j) return Select(a,p,i,k);
      else return Select(a,i+1,r,k-j);
}

关键的代码是：

for ( int i = 0; i<=(r-p-4)/5; i++ )//i即为n个元素的分组个数
      //将a[p+5*i]至a[p+5*i+4]的第3小元素与a[p+i]交换位置;
      //将中位数元素换至前面

一共(r-p+1)/5个组

注意这里i从0开始表示，为了方便交换时带入数组的下标，0-(r-p-4)/5，即一共(r-p-4)/5+1各组，即(r-p+1)/5个组

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<stack>
#include<algorithm>
using namespace std;

void bubbleSort(int a[],int p,int r){
    for(int i=p;i<r;i++){
        for(int j=i+1;j<=r;j++){
            if(a[j]<a[i])swap(a[i],a[j]);
        }
    }
}

int Partition(int a[],int p,int r,int val){
    int pos;
    for(int q=p;q<=r;q++){
        if(a[q]==val){pos=q;break;}
    }
    swap(a[p],a[pos]);

    int i=p,j=r+1,x=a[p];
    while(1){
        while(a[++i]<x&&i<r);
        while(a[--j]>x);
        if(i>=j)break;
        swap(a[i],a[j]);
    }
    a[p]=a[j];
    a[j]=x;
    return j;
}

int Select(int a[],int p,int r,int k){
    if(r-p<75){
        bubbleSort(a,p,r);
        return a[p+k-1];
    }

    for(int i=0;i<=(r-p-4)/5;i++){//把每个组的中位数交换到区间[p,p+(r-p-4)/4]
        int s=p+5*i,t=s+4;
        for(int j=0;j<3;j++){//冒泡排序，从后开始排，结果使得后三个数是排好顺序的（递增）
            for(int n=s;n<t-j;n++){
                if(a[n]>a[n+1])swap(a[n],a[n-1]);
            }
        }
        swap(a[p+i],a[s+2]);//交换每组中的中位数到前面
    }
    //(r-p-4)/5表示组数-1，则[p,p+(r-p-4)/5]的区间长度等于组数
    int x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10);//求中位数的中位数
    int i=Partition(a,p,r,x),j=i-p+1;
    if(k<=j)return Select(a,p,i,k);
    else return Select(a,i+1,r,k-j);
}
int main(){
    int x;
    //数组a存了0-79
    int a[80]={3,1,7,6,5,9,8,2,0,4,
               13,11,17,16,15,19,18,12,10,14,
               23,21,27,26,25,29,28,22,20,24,
               33,31,37,36,35,39,38,32,30,34,
               43,41,47,46,45,49,48,42,40,44,
               53,51,57,56,55,59,58,52,50,54,
               63,61,67,66,65,69,68,62,60,64,
               73,71,77,76,75,79,78,72,70,74,
              };
    while(scanf("%d",&x)!=EOF){
        printf("第%d大的数是%d\n",x,Select(a,0,79,x));
    }
}

qwq，博主nc写错输出了，“第i小的数”

更多常见问题的相关技术文章，请访问常见问题教程栏目进行学习！

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!