Comment implémenter le clustering Canopy en Python

L'algorithme Canopy a été proposé par Andrew McCallum, Kamal Nigam et Lyle Ungar en 2000. Il s'agit d'un prétraitement de l'algorithme de clustering k-means et de l'algorithme de clustering hiérarchique. Comme nous le savons tous, l'un des inconvénients des kmeans est que la valeur k doit être ajustée manuellement. La valeur k peut être finalement déterminée plus tard grâce à la méthode du coude et au coefficient de silhouette, mais ces méthodes sont jugées "ex post facto". , et le rôle de l'algorithme Canopy est de déterminer à l'avance le nombre initial de centres de cluster et de points centraux de cluster pour l'algorithme k-means grâce à un clustering approximatif.

Package utilisé :

import math
import random
import numpy as np
from datetime import datetime
from pprint import pprint as p
import matplotlib.pyplot as plt

1. présentation sur un plan bidimensionnel).

Bien sûr, les données de grande dimension peuvent également être utilisées, et j'ai écrit l'algorithme de base de la canopée dans la classe. Plus tard, les données de n'importe quelle dimension peuvent être traitées via des appels directs, bien sûr uniquement en petite taille. batches , de gros lots de données peuvent être déplacés vers Mahout et Hadoop.

# 随机生成500个二维[0,1)平面点
dataset = np.random.rand(500, 2)

Recommandations associées : "Tutoriel vidéo Python"

2. Générez ensuite deux catégories. Les attributs des classes sont les suivants : <. 🎜>

class Canopy:
    def __init__(self, dataset):        
        self.dataset = dataset        
        self.t1 = 0
      self.t2 = 0

Ajoutez le réglage des valeurs initiales de t1 et t2 et la fonction de taille

   # 设置初始阈值  
def setThreshold(self, t1, t2):        
    if t1 > t2:
        self.t1 = t1            
        self.t2 = t2        
    else:
        print('t1 needs to be larger than t2!')

3 Calcul de la distance, la méthode de calcul de la distance entre chaque point central est la distance euclidienne. .

#使用欧式距离进行距离的计算
def euclideanDistance(self, vec1, vec2):        
    return math.sqrt(((vec1 - vec2)**2).sum())

4. Ensuite, écrivez une fonction qui sélectionne aléatoirement les indices de l'ensemble de données en fonction de la longueur de l'ensemble de données

# 根据当前dataset的长度随机选择一个下标 
def getRandIndex(self):        
    return random.randint(0, len(self.dataset) - 1)

5.

def clustering(self):        
        if self.t1 == 0:
            print('Please set the threshold.')        
        else:
            canopies = []  # 用于存放最终归类结果
            while len(self.dataset) != 0:
                rand_index = self.getRandIndex()
                current_center = self.dataset[rand_index]  # 随机获取一个中心点，定为P点
                current_center_list = []  # 初始化P点的canopy类容器
                delete_list = []  # 初始化P点的删除容器
                self.dataset = np.delete(                    
                     self.dataset, rand_index, 0)  # 删除随机选择的中心点P
                for datum_j in range(len(self.dataset)):
                    datum = self.dataset[datum_j]
                    distance = self.euclideanDistance(
                        current_center, datum)  # 计算选取的中心点P到每个点之间的距离
                    if distance < self.t1:
                        # 若距离小于t1，则将点归入P点的canopy类
                        current_center_list.append(datum)                    
                    if distance < self.t2:
                        delete_list.append(datum_j)  # 若小于t2则归入删除容器
                # 根据删除容器的下标，将元素从数据集中删除
                self.dataset = np.delete(self.dataset, delete_list, 0)
                canopies.append((current_center, current_center_list))        
          return canopies

Afin de faciliter la visualisation ultérieure des données, les auvents que je définis ici sont un tableau. Bien sûr, dict peut également être utilisé.

Fonction 6.main()

def main():
    t1 = 0.6
    t2 = 0.4
    gc = Canopy(dataset)
    gc.setThreshold(t1, t2)
    canopies = gc.clustering()
    print('Get %s initial centers.' % len(canopies))    
    #showCanopy(canopies, dataset, t1, t2)

Code de visualisation du clustering Canopy

def showCanopy(canopies, dataset, t1, t2):
    fig = plt.figure()
    sc = fig.add_subplot(111)
    colors = ['brown', 'green', 'blue', 'y', 'r', 'tan', 'dodgerblue', 'deeppink', 'orangered', 'peru', 'blue', 'y', 'r',              'gold', 'dimgray', 'darkorange', 'peru', 'blue', 'y', 'r', 'cyan', 'tan', 'orchid', 'peru', 'blue', 'y', 'r', 'sienna']
    markers = [&#39;*&#39;, &#39;h&#39;, &#39;H&#39;, &#39;+&#39;, &#39;o&#39;, &#39;1&#39;, &#39;2&#39;, &#39;3&#39;, &#39;,&#39;, &#39;v&#39;, &#39;H&#39;, &#39;+&#39;, &#39;1&#39;, &#39;2&#39;, &#39;^&#39;,               &#39;<&#39;, &#39;>&#39;, &#39;.&#39;, &#39;4&#39;, &#39;H&#39;, &#39;+&#39;, &#39;1&#39;, &#39;2&#39;, &#39;s&#39;, &#39;p&#39;, &#39;x&#39;, &#39;D&#39;, &#39;d&#39;, &#39;|&#39;, &#39;_&#39;]    for i in range(len(canopies)):
        canopy = canopies[i]
        center = canopy[0]
        components = canopy[1]
        sc.plot(center[0], center[1], marker=markers[i],
                color=colors[i], markersize=10)
        t1_circle = plt.Circle(
            xy=(center[0], center[1]), radius=t1, color=&#39;dodgerblue&#39;, fill=False)
        t2_circle = plt.Circle(
            xy=(center[0], center[1]), radius=t2, color=&#39;skyblue&#39;, alpha=0.2)
        sc.add_artist(t1_circle)
        sc.add_artist(t2_circle)        for component in components:
            sc.plot(component[0], component[1],
                    marker=markers[i], color=colors[i], markersize=1.5)
    maxvalue = np.amax(dataset)
    minvalue = np.amin(dataset)
    plt.xlim(minvalue - t1, maxvalue + t1)
    plt.ylim(minvalue - t1, maxvalue + t1)
    plt.show()

Le rendu est le suivant :

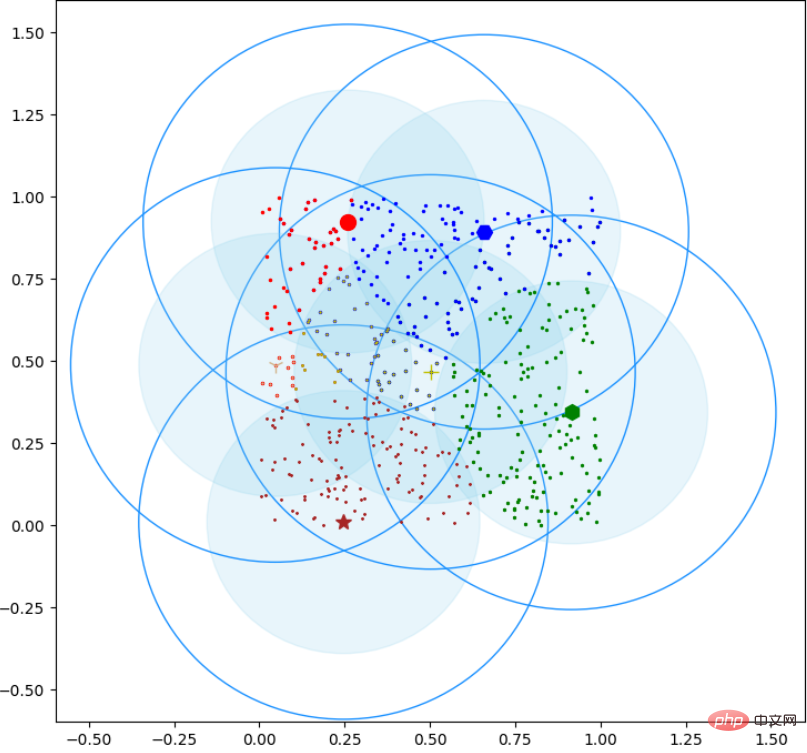
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!