Pourquoi les opérations à double virgule flottante perdent-elles en précision ?

Préface : Au travail, lorsqu'il s'agit d'addition, de soustraction, de multiplication et de division avec des points décimaux, ils penseront à utiliser BigDecimal pour le résoudre, mais beaucoup de gens ne comprennent pas pourquoi le double ou le float perdent en précision. Et comment résoudre BigDecimal ? Sans plus tarder, commençons.

1. Que sont les nombres à virgule flottante ?

Les nombres à virgule flottante sont un type de données utilisé par les ordinateurs pour représenter des décimales, en utilisant la notation scientifique. En Java, double est un nombre à virgule flottante double précision, 64 bits, et la valeur par défaut est 0,0d. float est un nombre à virgule flottante simple précision de 32 bits, la valeur par défaut est 0,0f

est stocké en mémoire

float Bit de signe (1 bit) ; Exposant (8 bits) Mantisse (23 bits)
bit de signe double (1 bit) Exposant (11 bits) Mantisse (52 bits)

L'exposant de float en mémoire est de 8 bits, car l'exposant le code stocke en fait le décalage de cadre de l'exposant, en supposant que la vraie valeur de l'exposant est e et que le code d'ordre est E, alors E=e+(2^n-1 -1). Parmi eux, 2^n-1 -1 est le décalage exponentiel spécifié par la norme IEEE754. Selon cette formule, nous pouvons obtenir 2^8 -1=127. Par conséquent, la plage des exposants de float est de -128 +127 et la plage des exposants de double est de -1024 +1023. L'exposant négatif détermine le nombre non nul avec la plus petite valeur absolue qu'un nombre à virgule flottante peut exprimer et l'exposant positif détermine le nombre avec la plus grande valeur absolue qu'un nombre à virgule flottante peut exprimer, c'est-à-dire qu'il détermine le plage de valeurs d’un nombre à virgule flottante.

La plage du float est de -2^128 ~ +2^127, soit -3,40E+38 ~ +3,40E+38 ; la plage de
double est de -2^1024 ; ~ + 2^1023, soit -1,79E+308 ~ +1,79E+308

2 Entrer dans la notation scientifique de la distorsion

Parlons d'abord de la notation scientifique. Méthode de comptage simplifiée utilisée pour représenter approximativement un très grand ou un petit nombre avec un grand nombre de chiffres. Pour les valeurs avec de petits chiffres, la notation scientifique n'a aucun avantage, mais pour les valeurs avec un grand nombre de chiffres, la notation scientifique l'est. mieux. Les avantages de cette méthode sont très évidents. Par exemple : la vitesse de la lumière est de 3 000 000 000 mètres/seconde et la population mondiale est d'environ 6 100 000 000 d'habitants. Les grands nombres comme la vitesse de la lumière et la population mondiale sont très difficiles à lire et à écrire, donc la vitesse de la lumière peut être écrite sous la forme 3*10^8, et la population mondiale peut être écrite sous la forme 6,1*10^9. Ainsi, la calculatrice utilise la notation scientifique pour indiquer que la vitesse de la lumière est de 3E8 et que la population mondiale est d'environ 6,1E9.

Quand nous étions enfants, nous jouions avec des calculatrices et aimions additionner ou soustraire comme des fous. À la fin, la calculatrice affichait l'image ci-dessous. C'est le résultat affiché par la notation scientifique

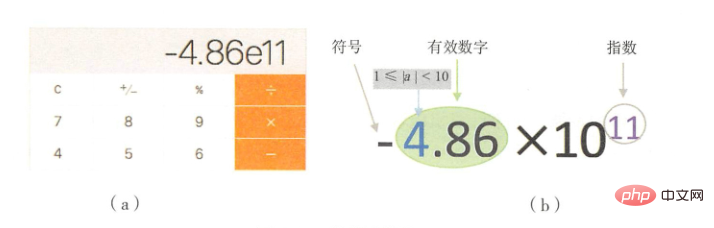
La valeur réelle sur l'image est -4,86*10^11=-486000000000. La notation scientifique décimale exige que la partie entière du chiffre significatif soit comprise dans l'intervalle [1, 9].

3. Entrez dans la précision de la distorsion

Le traitement informatique des données implique la conversion des données et diverses opérations complexes, telles que la conversion de différentes unités et de différentes bases (telles que. comme conversion décimale binaire), etc., de nombreuses opérations de division ne peuvent pas être divisées, comme 10÷3=3,3333...infini, mais la précision est limitée, 3,3333333x3 n'est pas égal à 10, la décimale obtenue après un traitement complexe Les données n'est pas précis, et plus la précision est élevée, plus elle est précise. La précision de float et double est déterminée par le nombre de chiffres dans la mantisse. La partie entière est toujours un "1" implicite puisqu'elle est inchangée, elle ne peut pas affecter la précision. float : 2^23 = 8388608, un total de sept chiffres Puisque le chiffre le plus à gauche est omis, cela signifie qu'il peut représenter jusqu'à 8 chiffres : 28388608 = 16777216. Il y a 8 chiffres significatifs, mais il est absolument garanti qu'il s'agit de 7 chiffres, c'est-à-dire que la précision du float est de 7 à 8 chiffres significatifs double : 2 ^ 52 = 4503599627370496, un total de 16 chiffres, de même, la précision du double ; est de 16 à 17 bits.

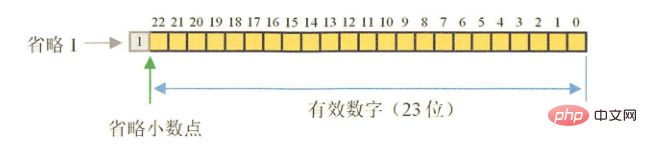
Lorsqu'il atteint une certaine valeur, il commence automatiquement à utiliser la notation scientifique et conserve les chiffres significatifs d'une précision pertinente, le résultat est donc un nombre approximatif et l'exposant est un nombre entier. Dans le système décimal, certaines décimales ne peuvent pas être entièrement exprimées en binaire. Par conséquent, il ne peut être représenté que par des bits limités, des erreurs peuvent donc se produire lors du stockage. Pour convertir des décimales décimales en binaires, utilisez la méthode de multiplication par 2 pour calculer. Après avoir supprimé la partie entière, les décimales restantes continuent d'être multipliées par 2 jusqu'à ce que les parties décimales soient toutes 0.

Si vous rencontrez

la sortie est 0,19999999999999998

double tapez 0,3-0,1. Vous devez convertir 0,3 en binaire dans l'opération

0,3 * 2 = 0,6 => .0 (.6), prendre 0 et laisser 0,6
0,6 * 2 = 1,2 => .01 (. 2) Prenez 1 et laissez 0,2
0,2 * 2 = 0,4 => .010 (.4) Prenez 0 et laissez 0,4
0,4 * 2 = 0,8 => .0100 (.8) Prenez 0 et laisse 0,8
0,8 * 2 = 1,6 => .01001 (.6) prend 1 et laisse 0,6
............

3. Résumé

Après avoir lu ce qui précède, il est probablement clair pourquoi les nombres à virgule flottante ont des problèmes de précision. En termes simples, les types float et double sont principalement conçus pour les calculs scientifiques et techniques. Ils effectuent des opérations binaires en virgule flottante, soigneusement conçues pour fournir des calculs de quasi-somme plus précis et plus rapides sur une large plage de valeurs. Cependant, ils ne fournissent pas de résultats totalement précis et ne doivent pas être utilisés pour obtenir des résultats précis. Les nombres à virgule flottante qui atteignent une certaine taille utiliseront automatiquement la notation scientifique. Une telle représentation n'est qu'une approximation du nombre réel mais n'est pas égale au nombre réel. Des boucles infinies ou un dépassement de la longueur de la mantisse à virgule flottante peuvent également se produire lors de la conversion de chiffres décimaux en binaires.

4. Alors, comment utiliser BigDecimal pour le résoudre ?

Regardez les deux sorties ci-dessous

Résultat de sortie :

0.299999999999999988897769753748434595763683319091796875
0 .3

Sur la photo Le plug-in de contrainte de code d'Alibaba a marqué un avertissement et m'a demandé d'utiliser la méthode constructeur des paramètres String pour créer BigDecimal. Étant donné que double ne peut pas être représenté exactement par 0,3 (tout binaire de longueur finie), la valeur transmise par le constructeur n'est pas exactement égale à 0,3. Lorsque vous utilisez BigDecimal, vous devez utiliser la méthode constructeur des paramètres String pour le créer. En parlant de ça, y a-t-il des bébés curieux qui se posent des questions, quel est le principe de BigDecimal ? Pourquoi n'y a-t-il aucun problème avec cela ? En fait, le principe est très simple. BigDecimal est immuable et peut être utilisé pour représenter des nombres décimaux signés de n'importe quelle précision. Le problème avec le double est que la conversion du point décimal en binaire perd en précision. Pendant le traitement, BigDecimal agrandit le nombre décimal de N fois afin qu'il puisse être calculé sur des nombres entiers et conserve les informations de précision correspondantes. Quant à la façon dont BigDecimal est enregistré, vous pouvez lire le code source.

Pour des articles plus techniques liés aux questions fréquemment posées, veuillez visiter la colonne FAQ pour en savoir plus !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!