
La méthode de recherche binaire, qui utilise pleinement la relation d'ordre entre les éléments et adopte la stratégie diviser pour régner, peut terminer la tâche de recherche en O(log n) dans le pire des cas.
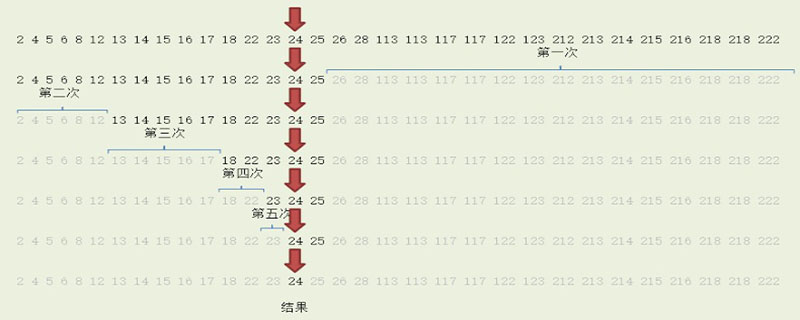
L'idée de base est de diviser n éléments en deux moitiés avec à peu près le même nombre, et de prendre un[n/2] et le nombre que vous vouloir trouver x est comparé Si x=a[n/2], x est trouvé et l’opération de l’algorithme se termine. (Apprentissage recommandé : Tutoriel vidéo Web front-end)
En informatique, la recherche binaire (anglais : recherche binaire), également connue sous le nom de recherche à demi-intervalle (anglais : demi-intervalle -recherche par intervalle) , La recherche logarithmique (anglais : recherche logarithmique) est un algorithme de recherche permettant de trouver un élément spécifique dans un tableau ordonné.
Le processus de recherche commence à partir de l'élément du milieu du tableau. Si l'élément du milieu se trouve être l'élément à trouver, le processus de recherche se termine si un élément spécifique est supérieur ou inférieur à l'élément du milieu, le processus de recherche se termine lorsque le tableau est supérieur ou inférieur à l'élément du milieu. Recherchez dans cette moitié et démarrez la comparaison à partir de l'élément du milieu comme auparavant.
Si le tableau est vide à une certaine étape, cela signifie qu'il est introuvable. Cet algorithme de recherche réduit la plage de recherche de moitié à chaque comparaison.
Si x
La méthode de recherche binaire est extrêmement largement utilisée et son idée est facile à comprendre, mais écrire un algorithme de recherche binaire correct n'est pas une tâche facile. Le premier algorithme de recherche binaire est apparu dès 1946, mais le premier algorithme de recherche binaire complètement correct n'est apparu qu'en 1962.
Bentley a écrit dans son livre "Writing Correct Programs" que 90 % des experts en informatique ne peuvent pas écrire un algorithme de recherche binaire complètement correct en 2 heures.
La clé du problème est de formuler avec précision les limites de chaque plage de recherche et de déterminer les conditions de terminaison, et de résumer correctement les différentes situations de nombres impairs et pairs. En fait, après l'avoir trié, nous pouvons trouver. que son algorithme spécifique est très intuitif.
Calcul de la complexité
Complexité temporelle : La recherche binaire coupe la zone de recherche de moitié à chaque fois, et il est évident que la complexité temporelle est O(log n). (n représente le nombre d'éléments dans l'ensemble)
Complexité spatiale : O(1). Bien que défini sous forme récursive, il est récursif en queue et peut être réécrit sous forme de boucle.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Le dernier classement des dix principales bourses du cercle des devises
Le dernier classement des dix principales bourses du cercle des devises
 Que faire si l'utilisation du processeur est trop élevée
Que faire si l'utilisation du processeur est trop élevée
 Quelle devise est l'USDT ?
Quelle devise est l'USDT ?
 Comment configurer l'hibernation dans le système Win7
Comment configurer l'hibernation dans le système Win7
 Que sont les instructions de contrôle de flux Java ?
Que sont les instructions de contrôle de flux Java ?
 Méthode d'implémentation de la fonction de lecture en ligne Python
Méthode d'implémentation de la fonction de lecture en ligne Python
 utilisation de la fonction de palette de couleurs Matlab
utilisation de la fonction de palette de couleurs Matlab
 Connecté mais impossible d'accéder à Internet
Connecté mais impossible d'accéder à Internet