 base de données
base de données
 tutoriel mysql
tutoriel mysql
 Pourquoi MySQL choisit-il l'arborescence B+ comme structure d'index ? (explication détaillée)
Pourquoi MySQL choisit-il l'arborescence B+ comme structure d'index ? (explication détaillée)
Pourquoi MySQL choisit-il l'arborescence B+ comme structure d'index ? (explication détaillée)
Dans MySQL, Innodb et MyIsam utilisent l'arborescence B+ comme structure d'index (les autres index tels que le hachage ne sont pas pris en compte ici). Cet article commencera par l'arbre de recherche binaire le plus courant, et expliquera progressivement les problèmes résolus par divers arbres et les nouveaux problèmes rencontrés, expliquant ainsi pourquoi MySQL choisit l'arbre B+ comme structure d'index.

Un ou deux arbres de recherche binaires (BST) : déséquilibrés
L'arbre de recherche binaire (BST, Binary Search Tree), également appelé arbre de tri binaire, doit satisfaire sur la base d'un arbre binaire : la valeur de tous les nœuds du sous-arbre gauche de n'importe quel nœud n'est pas supérieure à la valeur du nœud racine, n'importe quel nœud La valeur de tous les nœuds du sous-arbre droit n'est pas inférieure à la valeur du nœud racine. Ce qui suit est un BST (source d'image).
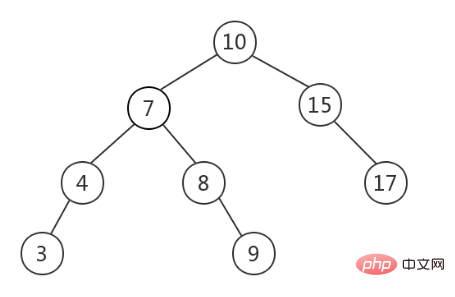
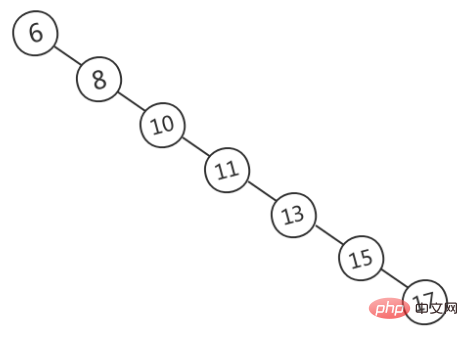
Lorsqu'une recherche rapide est requise, le stockage des données dans BST est un choix courant, car à ce stade, le temps de requête dépend de la hauteur de l'arbre et la complexité temporelle moyenne est O ( lgn). Cependant, BST peut devenir asymétrique et devenir déséquilibré, comme le montre la figure ci-dessous (source de l'image). À ce moment, BST dégénère en une liste chaînée et la complexité temporelle dégénère en). Sur).
Pour résoudre ce problème, des arbres binaires équilibrés sont introduits.
2. Arbre binaire équilibré (AVL) : rotation chronophage
L'arbre AVL est strictement équilibré Dans un arbre binaire, la différence de hauteur entre les sous-arbres gauche et droit de tous les nœuds ne peut pas dépasser 1 ; la recherche, l'insertion et la suppression de l'arborescence AVL sont O(lgn) dans le cas moyen et dans le pire des cas.
La clé pour atteindre l'équilibre dans AVL réside dans l'opération de rotation : l'insertion et la suppression peuvent détruire l'équilibre de l'arbre binaire, auquel cas l'arbre doit être rééquilibré par une ou plusieurs rotations d'arbre. Lors de l'insertion de données, une seule rotation (rotation simple ou double rotation) est requise au maximum ; mais lorsque les données sont supprimées, l'arborescence deviendra déséquilibrée. AVL doit maintenir l'équilibre de tous les nœuds sur le chemin à partir du nœud supprimé. au nœud racine. Rotation La magnitude de est O(lgn).
En raison de la rotation fastidieuse, l'arborescence AVL est très inefficace lors de la suppression de données lorsqu'il y a de nombreuses opérations de suppression, le coût de maintien de l'équilibre peut être élevé ; supérieurs aux avantages, l’AVL n’est donc pas largement utilisée dans la pratique.
3. Arbre rouge-noir : L'arbre est trop grand
Par rapport à l'arbre AVL, l'arbre rouge-noir ne poursuit pas un équilibre strict , mais il s'agit d'un équilibre approximatif : assurez-vous simplement que le chemin le plus long possible de la racine à la feuille n'est pas plus de deux fois plus long que le chemin le plus court possible. Du point de vue de la mise en œuvre, la plus grande caractéristique de l'arbre rouge-noir est que chaque nœud appartient à l'une des deux couleurs (rouge ou noir), et la division des couleurs des nœuds doit répondre à des règles spécifiques (les règles spécifiques sont omises) . Un exemple d'arbre rouge-noir est le suivant (source de l'image) :
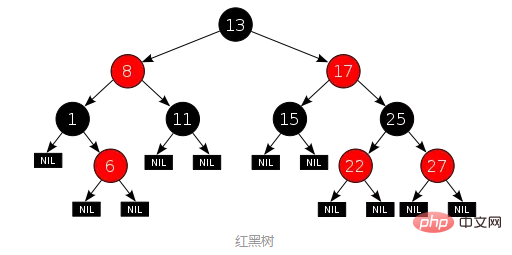
Par rapport à un arbre AVL, l'efficacité des requêtes d'un arbre rouge-noir diminuera. c'est parce que l'équilibre de l'arbre change. Cependant, l'efficacité de suppression de l'arbre rouge-noir a été grandement améliorée, car l'arbre rouge-noir introduit également de la couleur. Lors de l'insertion ou de la suppression de données, seul un nombre O(1) de rotations et de changements de couleur sont nécessaires pour assurer l'équilibre de base. . Il n'est pas nécessaire d'AVL L'arbre effectue un nombre de rotations O(lgn). En général, les performances statistiques des arbres rouge-noir sont supérieures à celles de l'AVL.
Par conséquent, dans les applications pratiques, les arbres AVL sont relativement rarement utilisés, tandis que les arbres rouge-noir sont très largement utilisés. Par exemple, TreeMap en Java utilise des arbres rouge-noir pour stocker des paires clé-valeur triées ; HashMap en Java8 utilise des listes chaînées + des arbres rouge-noir pour résoudre les problèmes de conflit de hachage (quand il y a moins de nœuds en conflit, utilisez des listes chaînées ; lorsqu'il y en a plus de nœuds conflictuels, utilisez un arbre rouge noir).
Pour les situations où les données sont en mémoire (telles que TreeMap et HashMap mentionnés ci-dessus), les performances des arbres rouge-noir sont très excellentes. Mais pour la situation où les données se trouvent dans des périphériques de stockage auxiliaires tels que des disques (tels que MySQL et d'autres bases de données), l'arbre rouge-noir n'est pas bon dans ce domaine, parce que l'arbre rouge-noir pousse encore trop haut . Lorsque les données sont sur le disque, les E/S du disque deviennent le plus gros goulot d'étranglement des performances, et l'objectif de conception doit être de minimiser le nombre d'E/S, plus la hauteur de l'arborescence est élevée, plus les ajouts, suppressions et modifications nécessitent de temps d'E/S. , et les recherches, ce qui affectera sérieusement les performances.
4. B-tree : Né pour les disques
BL'arbre est également appelé B-Arbre (où - n'est pas un signe moins) est un arbre de recherche équilibré multidirectionnel conçu pour les périphériques de stockage auxiliaires tels que les disques, par rapport aux arbres binaires, chaque nœud non-feuille de l'arbre B peut avoir plusieurs sous-arbres. Par conséquent, lorsque le nombre total de nœuds est le même, la hauteur de l'arbre B est beaucoup plus petite que l'arbre AVL et l'arbre rouge-noir (l'arbre B est un "nain"), et le nombre des E/S disque est considérablement réduite.
Le concept le plus important dans la définition d'un arbre B est l'ordre. Pour un arbre B d'ordre m, les conditions suivantes doivent être remplies :
- Chaque nœud contient au plus m nœuds enfants. .
- Si le nœud racine contient des nœuds enfants, il contient au moins 2 nœuds enfants ; à l'exception du nœud racine, chaque nœud non-feuille contient au moins m/2 nœuds enfants ;
- Un nœud non-feuille avec k enfants contiendra k - 1 enregistrements.
- Tous les nœuds feuilles sont dans la même couche.
On peut voir que la définition de B-tree limite principalement le nombre de nœuds enfants et d'enregistrements de nœuds non-feuilles.
L'image ci-dessous est un exemple d'arbre B à 3 ordres (source de l'image) :
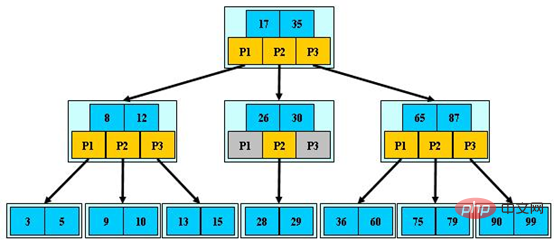
Les avantages du B-tree ne sont pas seulement minimes la hauteur de l'arbre, mais aussi la capacité d'accéder aux parties locales. Utilisation des principes sexuels. Le principe dit de localité signifie que lorsqu'une donnée est utilisée, les données à proximité ont une plus grande probabilité d'être utilisées dans un court laps de temps. B-tree stocke les données avec des clés similaires dans le même nœud. Lors de l'accès à l'une des données, la base de données lit le nœud entier dans le cache ; lorsque ses données adjacentes sont accédées immédiatement, elles peuvent être lues directement à partir du cache. aucune E/S disque n'est requise ; en d'autres termes, le taux de réussite du cache de B-tree est plus élevé.
B-tree a certaines applications dans les bases de données. Par exemple, l'index de mongodb utilise la structure B-tree. Cependant, dans de nombreuses applications de bases de données, des arbres B+, une variante du B-tree, sont utilisés.
5. L'arbre B+
L'arbre B+ est également un arbre de recherche équilibré à chemins multiples. Sa principale différence avec l'arbre B est :
- Chaque nœud de l'arbre B (y compris les nœuds feuilles et les nœuds non feuilles) stocke des données réelles. Seuls les nœuds feuilles de l'arbre B+ stockent des données réelles, et les nœuds non feuilles stockent uniquement les clés. Dans MySQL, les données réelles mentionnées ici peuvent être toutes les données de la ligne (comme l'index clusterisé d'Innodb), ou simplement la clé primaire de la ligne (comme l'index auxiliaire d'Innodb), ou l'adresse de la ligne ( comme l'index non clusterisé de MyIsam).
- Un enregistrement dans l'arbre B n'apparaîtra qu'une seule fois et n'apparaîtra pas de manière répétée, tandis que la clé de l'arbre B+ peut apparaître à plusieurs reprises - elle apparaîtra certainement dans un nœud feuille, ou elle peut apparaître à plusieurs reprises dans un nœud non -nœud feuille.
- Les nœuds feuilles de l'arbre B+ sont liés via une liste doublement chaînée.
- Pour les nœuds non-feuilles dans l'arbre B, le nombre d'enregistrements est inférieur de 1 au nombre de nœuds enfants tandis que le nombre d'enregistrements dans l'arbre B+ est le même que le nombre de nœuds enfants ;
Ainsi, l'arbre B+ présente les avantages suivants par rapport à l'arbre B :
- Moins de temps d'IO : Le non- les nœuds feuilles de l'arbre B+ ne contiennent que des clés, pas des données réelles, donc le nombre d'enregistrements stockés dans chaque nœud est bien supérieur au nombre de B (c'est-à-dire que l'ordre m est plus grand), donc la hauteur de l'arbre B+ est inférieur et le temps d'accès est inférieur. Moins de temps d'E/S sont nécessaires. De plus, puisque chaque nœud stocke plus d’enregistrements, le principe de localité d’accès est mieux utilisé et le taux de réussite du cache est plus élevé.
- est plus adapté aux requêtes de plage : Lorsque vous effectuez une requête de plage dans un arbre B, recherchez d'abord la limite inférieure à trouver, puis effectuez une recherche dans -ordre de parcours de l'arbre B jusqu'à trouver la limite supérieure de la recherche et la requête de plage de l'arbre B+ n'a besoin que de parcourir la liste chaînée.
- Efficacité des requêtes plus stables : La complexité temporelle de la requête de B-tree est comprise entre 1 et la hauteur de l'arbre (correspondant respectivement au nœud racine et au nœud feuille), La complexité des requêtes de l’arbre B+ est stable à la hauteur de l’arbre, car toutes les données se trouvent dans les nœuds feuilles.
Les arbres B+ présentent également des inconvénients : comme les clés apparaissent de manière répétée, elles prennent plus de place. Cependant, par rapport aux avantages en termes de performances, le désavantage en termes d'espace est souvent acceptable, de sorte que les arbres B+ sont plus largement utilisés dans les bases de données que les arbres B.
6. Ressentez la puissance de l'arbre B+
Comme mentionné précédemment, comparé aux arbres binaires tels que les arbres rouge-noir, l'arbre B L'arbre /B+ a le plus grand. L'avantage est que la hauteur de l'arbre est plus petite. En fait, pour l'indice B+ d'Innodb, la hauteur de l'arbre est généralement de 2 à 4 niveaux. Faisons quelques estimations précises.
La hauteur de l'arbre est déterminée par la commande. Plus la commande est grande, plus l'arbre est court ; et la taille de la commande dépend du nombre d'enregistrements que chaque nœud peut stocker. Chaque nœud d'Innodb utilise une page (page), la taille de la page est de 16 Ko, dont les métadonnées ne représentent qu'environ 128 octets (y compris les informations d'en-tête de gestion de fichiers, les informations d'en-tête de page, etc.), la majeure partie de l'espace est utilisée pour stocker des données. .
Pour les nœuds non-feuilles, l'enregistrement contient uniquement la clé de l'index et un pointeur vers le nœud de niveau suivant. En supposant que chaque page de nœud non-feuille stocke 1 000 enregistrements, chaque enregistrement occupe environ 16 octets ; cette hypothèse est raisonnable lorsque l'index est un entier ou une chaîne plus courte ; Par extension, nous entendons souvent des suggestions selon lesquelles la longueur de la colonne d'index ne devrait pas être trop grande. Voici la raison : si la colonne d'index est trop longue et que chaque nœud contient trop peu d'enregistrements, l'arbre sera trop haut et l'effet d'indexation sera atteint. sera considérablement réduit et l'index gaspillera plus d'espace.
- Pour les nœuds feuilles, l'enregistrement contient la clé et la valeur de l'index (la valeur peut être la clé primaire de la ligne, une ligne complète de données, etc., voir l'article précédent pour plus de détails), et la quantité de données est plus grande. On suppose ici que chaque page de nœud feuille stocke 100 enregistrements (en fait, lorsque l'index est un index clusterisé, ce nombre peut être inférieur à 100 ; lorsque l'index est un index auxiliaire, ce nombre peut être bien supérieur à 100 ; il peut être estimé en fonction de la situation réelle).
Pour un arbre B+ à 3 couches, la première couche (nœud racine) a 1 page et peut stocker 1000 enregistrements ; la deuxième couche a 1000 pages et peut stocker 1000*1000 enregistrements ; (nœud feuille) a 1 000*1 000 pages, et chaque page peut stocker 100 enregistrements, elle peut donc stocker 1 000*1 000*100 enregistrements, soit 100 millions d'enregistrements. Pour un arbre binaire, environ 26 couches sont nécessaires pour stocker 100 millions d'enregistrements.
7. Résumé
Enfin, résumez les problèmes résolus par les différents arbres et les nouveaux problèmes rencontrés :
1) , Binary Search Tree (BST) : résout le problème de base du tri, mais comme l'équilibre ne peut pas être garanti, il peut dégénérer en une liste chaînée
2), Balanced Binary Tree (AVL) : résout le problème de équilibre par rotation, mais l'efficacité de l'opération de rotation est trop faible ;
3) Arbre rouge-noir : en abandonnant l'équilibre strict et en introduisant des nœuds rouge-noir, le problème de l'efficacité de rotation AVL trop faible est cependant résolu. , dans des scénarios tels que les disques, l'arbre est toujours trop élevé, trop de fois IO
4), B-tree : en changeant l'arbre binaire en un arbre de recherche équilibré multi-chemins, le problème de l'arbre ; être trop élevé est résolu ;
5), B+ Tree : sur la base du B-tree, les nœuds non-feuilles sont transformés en nœuds d'index purs qui ne stockent pas de données, réduisant encore la hauteur de l'arbre ; De plus, les nœuds feuilles sont connectés dans une liste chaînée à l'aide de pointeurs, ce qui rend les requêtes de plage plus efficaces.
Apprentissage recommandé : Tutoriel MySQL
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 MySQL: la facilité de gestion des données pour les débutants
Apr 09, 2025 am 12:07 AM
MySQL: la facilité de gestion des données pour les débutants
Apr 09, 2025 am 12:07 AM
MySQL convient aux débutants car il est simple à installer, puissant et facile à gérer les données. 1. Installation et configuration simples, adaptées à une variété de systèmes d'exploitation. 2. Prise en charge des opérations de base telles que la création de bases de données et de tables, d'insertion, d'interrogation, de mise à jour et de suppression de données. 3. Fournir des fonctions avancées telles que les opérations de jointure et les sous-questionnaires. 4. Les performances peuvent être améliorées par l'indexation, l'optimisation des requêtes et le partitionnement de la table. 5. Prise en charge des mesures de sauvegarde, de récupération et de sécurité pour garantir la sécurité et la cohérence des données.
 MySQL: Concepts simples pour l'apprentissage facile
Apr 10, 2025 am 09:29 AM
MySQL: Concepts simples pour l'apprentissage facile
Apr 10, 2025 am 09:29 AM
MySQL est un système de gestion de base de données relationnel open source. 1) Créez une base de données et des tables: utilisez les commandes CreateDatabase et CreateTable. 2) Opérations de base: insérer, mettre à jour, supprimer et sélectionner. 3) Opérations avancées: jointure, sous-requête et traitement des transactions. 4) Compétences de débogage: vérifiez la syntaxe, le type de données et les autorisations. 5) Suggestions d'optimisation: utilisez des index, évitez de sélectionner * et utilisez les transactions.
 Comment ouvrir phpmyadmin
Apr 10, 2025 pm 10:51 PM
Comment ouvrir phpmyadmin
Apr 10, 2025 pm 10:51 PM
Vous pouvez ouvrir PHPMYADMIN via les étapes suivantes: 1. Connectez-vous au panneau de configuration du site Web; 2. Trouvez et cliquez sur l'icône PHPMYADMIN; 3. Entrez les informations d'identification MySQL; 4. Cliquez sur "Connexion".
 Comment créer Navicat Premium
Apr 09, 2025 am 07:09 AM
Comment créer Navicat Premium
Apr 09, 2025 am 07:09 AM
Créez une base de données à l'aide de NAVICAT Premium: Connectez-vous au serveur de base de données et entrez les paramètres de connexion. Cliquez avec le bouton droit sur le serveur et sélectionnez Créer une base de données. Entrez le nom de la nouvelle base de données et le jeu de caractères spécifié et la collation. Connectez-vous à la nouvelle base de données et créez le tableau dans le navigateur d'objet. Cliquez avec le bouton droit sur le tableau et sélectionnez Insérer des données pour insérer les données.
 MySQL et SQL: Compétences essentielles pour les développeurs
Apr 10, 2025 am 09:30 AM
MySQL et SQL: Compétences essentielles pour les développeurs
Apr 10, 2025 am 09:30 AM
MySQL et SQL sont des compétences essentielles pour les développeurs. 1.MySQL est un système de gestion de base de données relationnel open source, et SQL est le langage standard utilisé pour gérer et exploiter des bases de données. 2.MySQL prend en charge plusieurs moteurs de stockage via des fonctions de stockage et de récupération de données efficaces, et SQL termine des opérations de données complexes via des instructions simples. 3. Les exemples d'utilisation comprennent les requêtes de base et les requêtes avancées, telles que le filtrage et le tri par condition. 4. Les erreurs courantes incluent les erreurs de syntaxe et les problèmes de performances, qui peuvent être optimisées en vérifiant les instructions SQL et en utilisant des commandes Explication. 5. Les techniques d'optimisation des performances incluent l'utilisation d'index, d'éviter la numérisation complète de la table, d'optimiser les opérations de jointure et d'améliorer la lisibilité du code.
 Comment créer une nouvelle connexion à MySQL dans Navicat
Apr 09, 2025 am 07:21 AM
Comment créer une nouvelle connexion à MySQL dans Navicat
Apr 09, 2025 am 07:21 AM
Vous pouvez créer une nouvelle connexion MySQL dans NAVICAT en suivant les étapes: ouvrez l'application et sélectionnez une nouvelle connexion (CTRL N). Sélectionnez "MySQL" comme type de connexion. Entrez l'adresse Hostname / IP, le port, le nom d'utilisateur et le mot de passe. (Facultatif) Configurer les options avancées. Enregistrez la connexion et entrez le nom de la connexion.
 Comment récupérer les données après que SQL supprime les lignes
Apr 09, 2025 pm 12:21 PM
Comment récupérer les données après que SQL supprime les lignes
Apr 09, 2025 pm 12:21 PM
La récupération des lignes supprimées directement de la base de données est généralement impossible à moins qu'il n'y ait un mécanisme de sauvegarde ou de retour en arrière. Point clé: Rollback de la transaction: Exécutez Rollback avant que la transaction ne s'engage à récupérer les données. Sauvegarde: la sauvegarde régulière de la base de données peut être utilisée pour restaurer rapidement les données. Instantané de la base de données: vous pouvez créer une copie en lecture seule de la base de données et restaurer les données après la suppression des données accidentellement. Utilisez la déclaration de suppression avec prudence: vérifiez soigneusement les conditions pour éviter la suppression accidentelle de données. Utilisez la clause WHERE: Spécifiez explicitement les données à supprimer. Utilisez l'environnement de test: testez avant d'effectuer une opération de suppression.
 Comment utiliser un seul fileté redis
Apr 10, 2025 pm 07:12 PM
Comment utiliser un seul fileté redis
Apr 10, 2025 pm 07:12 PM
Redis utilise une architecture filetée unique pour fournir des performances élevées, une simplicité et une cohérence. Il utilise le multiplexage d'E / S, les boucles d'événements, les E / S non bloquantes et la mémoire partagée pour améliorer la concurrence, mais avec des limites de limitations de concurrence, un point d'échec unique et inadapté aux charges de travail à forte intensité d'écriture.





