 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Trouver la somme des plus grands diviseurs impairs en utilisant PHP
Trouver la somme des plus grands diviseurs impairs en utilisant PHP
Trouver la somme des plus grands diviseurs impairs en utilisant PHP
Cet article explique comment trouver la somme des plus grands diviseurs impairs en utilisant PHP. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer. J'espère qu'il sera utile à tout le monde.

Xiao Yi est un passionné de théorie des nombres et s'intéresse beaucoup aux diviseurs impairs d'un nombre. Un jour, Xiaoyi a rencontré un tel problème : définissez la fonction f(x) comme le plus grand diviseur impair de x, et x est un entier positif. Par exemple : f(44) = 11.
Maintenant étant donné un N, nous devons trouver f(1) + f(2) + f(3)…….f(N)
Par exemple : N = 7
f(1) + f(2) + f(3) + f(4) + f(5) + f(6) + f(7) = 1 + 1 + 3 + 1 + 5 + 3 + 7 = 21
Xiao Yi a rencontré des difficultés pour calculer ce problème et a besoin de vous pour concevoir un algorithme pour l'aider.
<?php
$num = trim(fgets(STDIN));
function jNum($num){
$m = $num/2;
$res = 1;
if($num&0x1 == 1){//如果他本身就是个奇数,那么他的最大奇约数就是他本身
$res = $num;
goto HELL;
}
for($i = 1; $i<=$m; $i=$i+2){//如果不是,那么就从1开始一直往上除,每次+2(奇数)
if($num%$i==0){
$res = $i;
}
}
HELL:
return $res;
}
function jNum2($num)
{
$res = 0;
for($i=1;$i<=$num;$i++){
if(($i&0x1) == 1){//如果他本身就是个奇数,那么他的最大奇约数就是他本身
$res+=$i;
}else{
$n = $i;
while(true){//优化,从最大的数开始往下除
$n = $n>>1;
if(($n&0x1) == 1){
$res+=$n;
break;
}
}
}
}
HELL:
return $res;
}
function jNum3($num){//公式法
if($num == 1){
return 1;
}
if(($num&0x1) == 0){
return jNum3($num>>1)+$num*$num/4;
}else{
return jNum3($num-1)+$num;
}
}
//$sum = 0;
//for($i = 1; $i<=$num; $i++){
// $sum+=jNum($i);
//}
//echo $sum;
//echo jNum2($num);
echo jNum3($num);Commencez avec la pensée conventionnelle, qui a été déboguée, expire toujours si vous la remplacez par la méthode 2, elle expire toujours.
Changez votre façon de penser. .
Dans le processus de recherche de somme(i), si i est un nombre impair, vous pouvez le trouver directement, qui est i lui-même, c'est-à-dire f(i) = i.
Le problème est de trouver la somme de tous les f(i), i est un nombre pair.
Parce que c'est le plus grand diviseur impair, donc f(2k) = f(k), donc f(2) + f(4) + … + f(2k) = f(1) + f( 2 ) + … + f(k);
Par conséquent, il n'est pas facile de penser à la formule générale
en utilisant l'induction mathématique. . . Une telle question BT. .
Cet article est reproduit à partir de : https://blog.csdn.net/qq_28602957/article/details/77914402
Apprentissage recommandé : Tutoriel vidéo PHP
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Configuration du projet CakePHP
Sep 10, 2024 pm 05:25 PM
Configuration du projet CakePHP
Sep 10, 2024 pm 05:25 PM
Dans ce chapitre, nous comprendrons les variables d'environnement, la configuration générale, la configuration de la base de données et la configuration de la messagerie dans CakePHP.
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
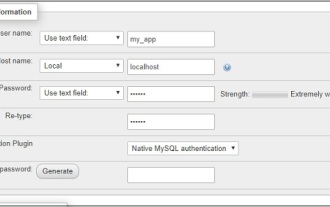 CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
CakePHP travaillant avec la base de données
Sep 10, 2024 pm 05:25 PM
Travailler avec la base de données dans CakePHP est très simple. Nous comprendrons les opérations CRUD (Créer, Lire, Mettre à jour, Supprimer) dans ce chapitre.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
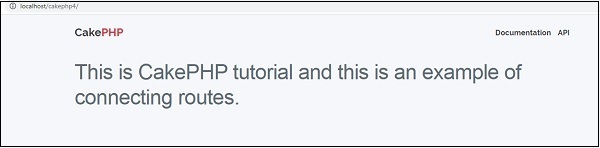 Routage CakePHP
Sep 10, 2024 pm 05:25 PM
Routage CakePHP
Sep 10, 2024 pm 05:25 PM
Dans ce chapitre, nous allons apprendre les sujets suivants liés au routage ?
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
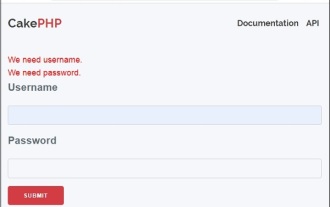 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.






