
Quels sont les algorithmes de tri en Python ? L'article suivant vous présentera les dix principaux algorithmes de tri classiques en Python. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer. J'espère qu'il sera utile à tout le monde.

Maintenant, beaucoup de choses peuvent être résolues par des algorithmes. En programmation, les algorithmes jouent un rôle très important. L'encapsulation des algorithmes avec des fonctions rend le programme meilleur, pas besoin d'écrire à plusieurs reprises.
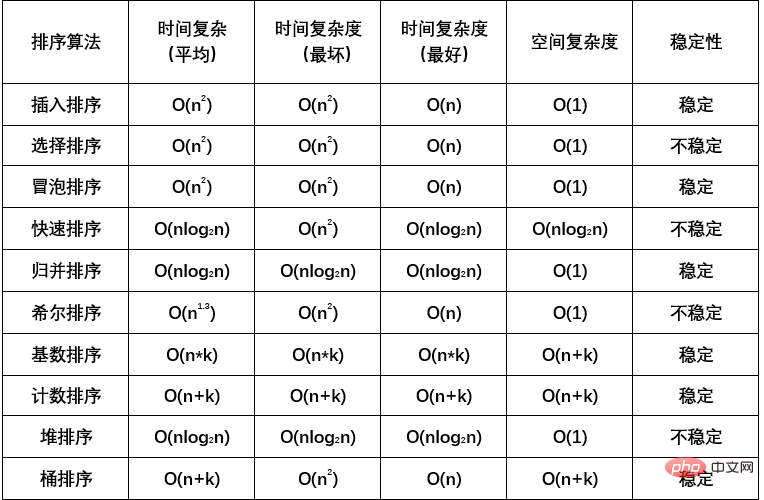
Dix algorithmes classiques de Python :
1. 🎜>
1. Idée d'algorithme
Partez du deuxième élément et comparez-le avec l'élément précédent si l'élément précédent est plus grand que l'élément actuel. , puis Déplacez l'élément précédent en arrière, et l'élément actuel en avant tour à tour, jusqu'à ce qu'un élément plus petit ou égal à lui soit trouvé et inséré derrière lui, Sélectionnez ensuite le troisième élément, répétez l'opération ci-dessus, insérez , et sélectionnez tour à tour Le dernier élément, après insertion, termine tout le tri.2. Implémentation du code
def insertion_sort(arr):
#插入排序
# 第一层for表示循环插入的遍数
for i in range(1, len(arr)):
# 设置当前需要插入的元素
current = arr[i]
# 与当前元素比较的比较元素
pre_index = i - 1
while pre_index >= 0 and arr[pre_index] > current:
# 当比较元素大于当前元素则把比较元素后移
arr[pre_index + 1] = arr[pre_index]
# 往前选择下一个比较元素
pre_index -= 1
# 当比较元素小于当前元素,则将当前元素插入在 其后面
arr[pre_index + 1] = current
return arr2. Tri de sélection
1. Idée d'algorithme
Supposons que le premier élément soit l'élément de comparaison, comparez-le tour à tour avec les éléments suivants, trouvez le plus petit élément après avoir comparé tous les éléments, échangez-le avec le premier élément et répétez l'opération ci-dessus . Nous trouvons le deuxième plus petit élément et l'échangeons avec l'élément en deuxième position, et ainsi de suite pour trouver le plus petit élément restant et le déplaçons vers l'avant, c'est-à-dire que le tri est terminé.2. Implémentation du code
def selection_sort(arr):
#选择排序
# 第一层for表示循环选择的遍数
for i in range(len(arr) - 1):
# 将起始元素设为最小元素
min_index = i
# 第二层for表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(arr)):
if arr[j] < arr[min_index]:
# 如果当前元素比最小元素小,则把当前元素角标记为最小元素角标
min_index = j
# 查找一遍后将最小元素与起始元素互换
arr[min_index], arr[i] = arr[i], arr[min_index]
return arr3. Tri à bulles
1 . Idée algorithmique
Commencez à comparer le premier et le deuxième, si le premier est plus grand que le deuxième, échangez les positions, puis comparez le deuxième et le troisième, et revenez progressivement en arrière. premier tour, le plus grand élément a été classé dernier, Donc si l'opération ci-dessus est répétée, le deuxième plus grand élément sera classé avant-dernier. , puis répétez l'opération ci-dessus n-1 fois pour terminer le tri, car il n'y a qu'un seul élément la dernière fois, aucune comparaison n'est donc nécessaire.2. Implémentation du code
def bubble_sort(arr):
#冒泡排序
# 第一层for表示循环的遍数
for i in range(len(arr) - 1):
# 第二层for表示具体比较哪两个元素
for j in range(len(arr) - 1 - i):
if arr[j] > arr[j + 1]:
# 如果前面的大于后面的,则交换这两个元素的位置
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr4. Tri rapide
1. Idée algorithmique
Trouvez la condition de base, qui doit être la plus simple possible, et continuez à décomposer le problème (ou à réduire la taille) jusqu'à ce que la condition de base soit remplie.2. Implémentation du code
def quick_sort(arr):
if len(arr) < 2:
# 基线条件:为空或只包含一个元素的数组是“有序”的
return arr
else:
# 递归条件
pivot = arr[0]
# 由所有小于基准值的元素组成的子数组
less = [i for i in arr[1:] if i <= pivot]
# 由所有大于基准值的元素组成的子数组
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print(quick_sort([10, 5, 2, 3]))5. Tri par fusion
1. Idée d'algorithme
Le tri par fusion est une application typique de la méthode diviser pour régner. Méthode Divide-and-Conquer (pide-and-Conquer) : divisez le problème d'origine en n sous-problèmes plus petits avec une structure similaire au problème d'origine, résolvez ces problèmes de manière récursive, puis combinez les résultats pour obtenir la solution à l'original ; problème. La séquence décomposée ressemble à un arbre binaire. Étapes spécifiques de mise en œuvre :2. Implémentation du code
def merge_sort(arr):
#归并排序
if len(arr) == 1:
return arr
# 使用二分法将数列分两个
mid = len(arr) // 2
left = arr[:mid]
right = arr[mid:]
# 使用递归运算
return marge(merge_sort(left), merge_sort(right))
def marge(left, right):
#排序合并两个数列
result = []
# 两个数列都有值
while len(left) > 0 and len(right) > 0:
# 左右两个数列第一个最小放前面
if left[0] <= right[0]:
result.append(left.pop(0))
else:
result.append(right.pop(0))
# 只有一个数列中还有值,直接添加
result += left
result += right
return result6. 🎜>1. Idée d'algorithme
L'idée générale du tri Hill est de trier plusieurs éléments à un intervalle fixe puis de réduire cet intervalle. De cette façon, la séquence finale devient une séquence ordonnée de base. Étapes spécifiques :
Calculer une valeur d'incrément (intervalle)
Comparer des éléments avec des incréments, Par exemple, si le la valeur d'incrément est 7, puis insérez les éléments de tri 0, 7, 14, 21...
puis triez 1, 8, 15..., et triez-les par ordre croissant.
Une fois tous les éléments triés, réduisez l'incrément à, par exemple, 3, puis répétez les étapes 2 et 3 ci-dessus
Enfin, réduisez l'incrément de 1, la séquence est fondamentalement dans l'ordre, et la dernière insertion ordinaire peut être effectuée
def shell_sort(arr):
#希尔排序
# 取整计算增量(间隔)值
gap = len(arr) // 2
while gap > 0:
# 从增量值开始遍历比较
for i in range(gap, len(arr)):
j = i
current = arr[i]
# 元素与他同列的前面的每个元素比较,如果比前面的小则互换
while j - gap >= 0 and current < arr[j - gap]:
arr[j] = arr[j - gap]
j -= gap
arr[j] = current
# 缩小增量(间隔)值
gap //= 2
return arr7. Tri par base
1. Idée d'algorithme
Le tri par base (tri par base) appartient au "tri par distribution". Également connu sous le nom de « tri par compartiment » ou tri par bac, comme son nom l'indique, il alloue les éléments à trier dans certains « compartiments » via une partie des informations de valeur clé pour obtenir l'effet de tri Radix. Il s'agit d'un tri stable, et sa complexité temporelle est O (nlog(r)m), où r est la base prise et m est le nombre de tas. À certains moments, l'efficacité de la méthode de tri par base est supérieure à celle des autres méthodes de classement sexuel. .
2. Implémentation du code2.1 est transformé du tri par seau, du tri par seau du bit le plus bas au bit le plus élevé, et génère enfin la liste finale classée. def RadixSort(list,d):
for k in range(d):#d轮排序
# 每一轮生成10个列表
s=[[] for i in range(10)]#因为每一位数字都是0~9,故建立10个桶
for i in list:
# 按第k位放入到桶中
s[i//(10**k)%10].append(i)
# 按当前桶的顺序重排列表
list=[j for i in s for j in i]
return list
from random import randint
def radix_sort():
A = [randint(1, 99999999) for _ in xrange(9999)]
for k in xrange(8):
S = [ [] for _ in xrange(10)]
for j in A:
S[j / (10 ** k) % 10].append(j)
A = [a for b in S for a in b]
for i in A:
print i八、计数排序
1.算法思想
对每一个输入元素x,确定小于x的元素个数。利用这一信息,就可以直接把x 放在它在输出数组上的位置上了,运行时间为O(n),但其需要的空间不一定,空间浪费大。
2.代码实现
from numpy.random import randint
def Conuting_Sort(A):
k = max(A) # A的最大值,用于确定C的长度
C = [0]*(k+1) # 通过下表索引,临时存放A的数据
B = (len(A))*[0] # 存放A排序完成后的数组
for i in range(0, len(A)):
C[A[i]] += 1 # 记录A有哪些数字,值为A[i]的共有几个
for i in range(1, k+1):
C[i] += C[i-1] # A中小于i的数字个数为C[i]
for i in range(len(A)-1, -1, -1):
B[C[A[i]]-1] = A[i] # C[A[i]]的值即为A[i]的值在A中的次序
C[A[i]] -= 1 # 每插入一个A[i],则C[A[i]]减一
return B九、堆排序
1.算法思想
堆分为最大堆和最小堆,是完全二叉树。堆排序就是把堆顶的最大数取出,将剩余的堆继续调整为最大堆,具体过程在第二块有介绍,以递归实现 ,
剩余部分调整为最大堆后,再次将堆顶的最大数取出,再将剩余部分调整为最大堆,这个过程持续到剩余数只有一个时结束。
2.代码实现
import time,random
def sift_down(arr, node, end):
root = node
#print(root,2*root+1,end)
while True:
# 从root开始对最大堆调整
child = 2 * root +1 #left child
if child > end:
#print('break',)
break
print("v:",root,arr[root],child,arr[child])
print(arr)
# 找出两个child中交大的一个
if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
child += 1 #设置右边为大
if arr[root] < arr[child]:
# 最大堆小于较大的child, 交换顺序
tmp = arr[root]
arr[root] = arr[child]
arr[child]= tmp
# 正在调整的节点设置为root
#print("less1:", arr[root],arr[child],root,child)
root = child #
#[3, 4, 7, 8, 9, 11, 13, 15, 16, 21, 22, 29]
#print("less2:", arr[root],arr[child],root,child)
else:
# 无需调整的时候, 退出
break
#print(arr)
print('-------------')
def heap_sort(arr):
# 从最后一个有子节点的孩子还是调整最大堆
first = len(arr) // 2 -1
for i in range(first, -1, -1):
sift_down(arr, i, len(arr) - 1)
#[29, 22, 16, 9, 15, 21, 3, 13, 8, 7, 4, 11]
print('--------end---',arr)
# 将最大的放到堆的最后一个, 堆-1, 继续调整排序
for end in range(len(arr) -1, 0, -1):
arr[0], arr[end] = arr[end], arr[0]
sift_down(arr, 0, end - 1)
#print(arr)十、桶排序
1.算法思想
为了节省空间和时间,我们需要指定要排序的数据中最小以及最大的数字的值,来方便桶排序算法的运算。
2.代码实现
#桶排序
def bucket_sort(the_list):
#设置全为0的数组
all_list = [0 for i in range(100)]
last_list = []
for v in the_list:
all_list[v] = 1 if all_list[v]==0 else all_list[v]+1
for i,t_v in enumerate(all_list):
if t_v != 0:
for j in range(t_v):
last_list.append(i)
return last_list总结:
在编程中,算法都是相通的,算法重在算法思想,相当于将一道数学上的应用题的每个条件,区间,可能出现的结果进行分解,分步骤的实现它。算法就是将具体问题的共性抽象出来,将步骤用编程语言来实现。通过这次对排序算法的整理,加深了对各算法的了解,具体的代码是无法记忆的,通过对算法思想的理解,根据伪代码来实现具体算法的编程,才是真正了解算法。
推荐学习:Python视频教程
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!