 base de données
base de données
 tutoriel mysql
tutoriel mysql
 Compréhension approfondie du principe de l'index B+Tree de Mysql
Compréhension approfondie du principe de l'index B+Tree de Mysql
Compréhension approfondie du principe de l'index B+Tree de Mysql
Apr 28, 2020 pm 02:57 PMTout d'abord, la création correcte d'index appropriés est la base de l'amélioration des performances des requêtes de base de données.
Qu'est-ce qu'un indice ?
Un index est une structure de données de stockage décentralisée créée pour accélérer la récupération des lignes de données dans une table.
Comment fonctionne l'index ?
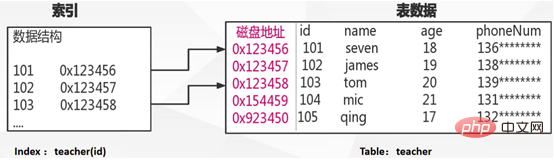
Comme le montre l'image ci-dessus, s'il y a une instruction SQL, sélectionnez * from professor où id = 101, s'il n'y en a pas index, Pour trouver cet enregistrement, nous devons analyser la table entière et faire correspondre les données avec id = 101. Si nous avons un index, nous pouvons trouver rapidement l'adresse de la ligne correspondant à 101 enregistrée sur le disque via l'index, puis récupérer les données de la ligne correspondante en fonction de l'adresse donnée.
Pourquoi la base de données MYSQL utilise-t-elle B+TREE comme structure de données d'index ?
Pour accélérer la récupération des données, la première chose qui vient à l'esprit est l'arbre binaire. La complexité temporelle de recherche de l'arbre binaire peut atteindre O(log2(n)). Jetons un coup d'œil à la structure de stockage de l'arbre binaire :
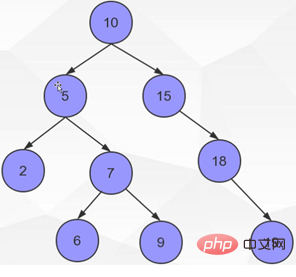
La recherche d'arbre binaire est équivalente à une recherche binaire. La recherche binaire peut grandement améliorer l'efficacité des requêtes, mais elle présente un problème : l'arborescence binaire utilise les premières données insérées comme nœud racine. Comme le montre la figure ci-dessus, si vous regardez uniquement le côté droit, vous constaterez que c'est le cas. est une structure de liste chaînée linéaire. Si nos données actuelles ne contiennent que 1, 2, 3, 4, 5, 6, la situation suivante se produira :
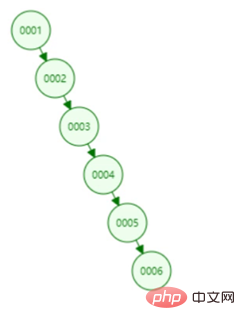
Si les données que nous voulons interroger sont 6, nous Besoin Ce n'est qu'en parcourant tous les nœuds que nous pouvons trouver 6, ce qui équivaut à une analyse complète de la table. En raison de ce problème, l'arbre de recherche binaire n'est pas adapté à une utilisation comme structure de données d'index.
Sur la base d'une telle déduction, afin de résoudre le problème de la liste chaînée linéaire, il est facile de penser à un arbre de recherche binaire équilibré. Voyons à quoi ressemble un arbre binaire équilibré :
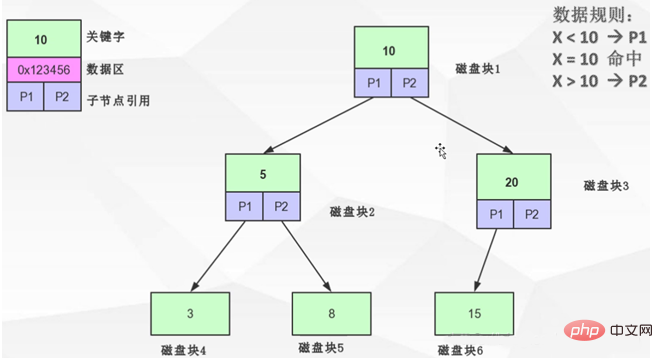
Un arbre binaire de recherche équilibré est défini comme : la différence de hauteur entre les nœuds enfants d'un nœud ne peut pas dépasser 1. , comme le montre le nœud 20 dans la figure ci-dessus, à gauche La hauteur du nœud est 1, la hauteur du nœud droit est 0 et la différence est 1, donc l'image ci-dessus ne viole pas la définition. C'est un arbre binaire équilibré. Les moyens d'assurer l'équilibre d'un arbre binaire sont les opérations à gauche, à droite et autres. Quant aux opérations à gauche et à droite, vous pouvez rechercher vous-même les connaissances pertinentes.
Si l'arbre binaire équilibré dans l'image ci-dessus enregistre l'index id, maintenant pour commencer avec les données avec id = 8, chargez d'abord le nœud racine dans la mémoire, comparez 8 et 10 et trouvez que 8 est inférieur à 10, continuez Chargez le sous-arbre gauche de 10. Chargez 5 dans la mémoire et comparez 8 avec 5. De la même manière, chargez le sous-arbre droit du nœud 5. A ce moment, un hit est trouvé, et maintenant les données correspondant à l'index avec l'identifiant 8 sont chargées.
Comment retrouver les données correspondant à l'index ?
Il existe généralement deux façons de sauvegarder des données dans un index La première consiste à sauvegarder tout le contenu spécifique des données de la ligne avec id = 8 dans la zone de données du nœud. D'une autre manière, la zone de données enregistre l'adresse du disque où les données sont réellement stockées.
À ce stade, l'arbre binaire équilibré résout le problème des listes chaînées linéaires. L'efficacité de la requête de données semble être bonne, atteignant essentiellement O(log2(n)). une structure de données ? Quel genre de problèmes a-t-il ?
Problème 1 : Efficacité de recherche insuffisante De manière générale, dans l'arborescence, la profondeur des données détermine le nombre d'IO lors de la recherche. Comme le montre la figure ci-dessus, la recherche de données avec id = 8 nécessite 3 IO. Lorsque la quantité de données atteindra des millions, la hauteur de l’arbre sera terrifiante.
Problème 2 : la requête n'est pas stable. Si les données interrogées tombent sur le nœud racine, une seule IO est requise. S'il s'agit d'un nœud feuille ou d'un nœud de branche, plusieurs IO seront nécessaires.
Problème 3 : Le nœud stocke trop peu de contenu de données. Il ne fait pas bon usage des fonctionnalités du système d'exploitation et d'échange de données sur disque, ni de la capacité de lecture anticipée des E/S du disque. Étant donné qu'un échange de données entre le système d'exploitation et le disque s'effectue en unités de page, une page = 4 Ko, c'est-à-dire que le système d'exploitation chargera des données 4 Ko dans la mémoire pour chaque E/S. Cependant, la structure de chaque nœud dans l'arborescence binaire n'enregistre qu'un seul mot-clé, une zone de données et deux références aux nœuds enfants, qui ne peuvent pas remplir 4 Ko de contenu. Heureusement, j'ai travaillé dur sur une opération IO, mais un seul mot-clé a été chargé. Lorsque la hauteur de l'arborescence est très élevée et que le mot-clé recherché se trouve sur un nœud feuille ou un nœud branche, la récupération prend plusieurs fois. un mot-clé.IO.
Existe-t-il une structure qui peut résoudre ce problème des arbres binaires ?
Oui, arbre de recherche équilibré multidirectionnel : (Arbre d'équilibre) :
L'arbre B est un arbre absolument équilibré, tous les nœuds feuilles sont à la même hauteur, comme indiqué dans l'image. figure ci-dessous :
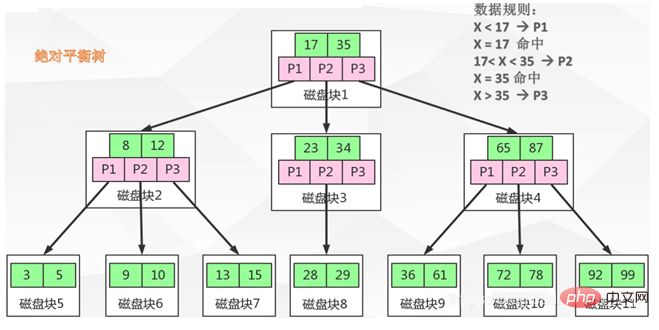
Quels sont les avantages de B Tree et comment résout-il certains problèmes ?
Regardons d'abord la définition. L'image ci-dessus montre un arbre 2-3 (chaque nœud stocke 2 mots-clés et a 3 voies. Un arbre de recherche équilibré à plusieurs voies signifie multi-fork). ce qui précède Comme le montre la figure, la relation entre le nombre de mots-clés enregistrés dans chaque nœud et le nombre de chemins est :
Nombre de mots-clés = nombre de chemins – 1.
Supposons que vous souhaitiez trouver les données avec l'identifiant = 28 à partir de l'image ci-dessus, le processus de recherche B TREE est le suivant :
Chargez d'abord le nœud racine dans la mémoire, puis chargez les deux mots-clés 17 et 35. La règle de jugement est la suivante :

Après avoir atteint 28 selon les règles ci-dessus, chargez les données correspondant à 28, puis recherchez la zone de données correspondant à 28. La zone de données stocke les données spécifiques ou un pointeur vers les données.
Pourquoi cette structure est-elle capable de résoudre le problème des arbres binaires équilibrés ?
peut faire bon usage des caractéristiques interactives du système d'exploitation et du disque Afin de faire bon usage de la capacité de lecture anticipée du disque, MYSQL définit la taille de la page à 16 Ko. consiste à définir la taille d'un nœud (bloc de disque) à 16 Ko, une IO charge le contenu d'un nœud (16 Ko) en mémoire. Ici, supposons que le type de mot-clé est int, qui fait 4 octets. Si la zone de données correspondant à chaque mot-clé fait également 4 octets, sans tenir compte de la référence des nœuds enfants, chaque nœud de la figure ci-dessus peut stocker environ ( 16 * 1000) / 8 = 2000 mots-clés, alors il y a 2001 façons au total. Pour un arbre binaire à trois niveaux de hauteur, jusqu'à 7 mots-clés peuvent être enregistrés. Cependant, pour cet arbre B à 2001 chemins, le nombre de mots-clés pouvant être recherchés avec trois niveaux de hauteur est bien supérieur à celui d'un arbre binaire à trois niveaux de hauteur. arbre binaire.
Dans le processus de B TREE assurant l'équilibre de l'arbre, chaque changement de mots-clés entraînera de grands changements dans la structure. Ce processus est particulièrement chronophage, donc lors de la création d'un index, vous devez créer un. index approprié. , au lieu de créer des index pour tous les champs, la création d'index redondants ne fera qu'augmenter la consommation de performances lors de l'ajout, de la suppression et de la modification de données.
Puisque B-tree a très bien résolu le problème, pourquoi MYSQL utilise-t-il toujours B+TREE ?
Regardons d'abord à quoi ressemble B+TREE. B+TREE est une variante de B TREE dans les espèces d'arbres B+, la relation entre le nombre de chemins dans les espèces d'arbres B et le nombre de. les mots-clés ne sont plus valables. , dans B+TREE, la règle de récupération des données utilise un intervalle fermé à gauche, et la relation entre le nombre de chemins et le nombre de clés est de 1:1, comme le montre la figure ci-dessous :
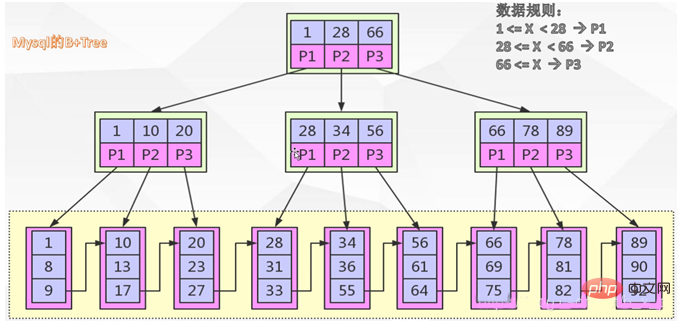
Si l'image ci-dessus est un index créé par ID. Si vous recherchez des données avec id = 1, les règles de recherche sont les suivantes :
 <.>
<.>
Quelle est la différence entre B TREE et B+TREE ?
1. La recherche par mot-clé B+TREE utilise l'intervalle fermé de gauche. La raison pour laquelle l'intervalle fermé de gauche est utilisé est qu'elle souhaite mieux prendre en charge les identifiants à incrémentation automatique. intention de mysql. Autrement dit, si id = 1 est trouvé, la recherche se poursuivra jusqu'à ce que 1 dans le nœud feuille soit trouvé. 2. Le nœud racine et le nœud de branche B+TREE n'ont pas de zone de données et les données correspondant au mot-clé ne sont enregistrées que dans le nœud feuille. Autrement dit, seule la zone de données de mot-clé dans le nœud feuille enregistrera le contenu réel des données ou l'adresse du contenu. Dans l'espèce d'arbre B, si le nœud racine est touché, les données seront renvoyées directement. Et dans B+TREE, les nœuds feuilles ne sauvegarderont pas les références aux nœuds enfants. 3. Les nœuds feuilles B+TREE sont disposés séquentiellement et les nœuds adjacents ont une relation de référence séquentielle. Comme le montre la figure ci-dessus, les nœuds feuilles sont connectés par des pointeurs.Pourquoi MYSQL a-t-il finalement choisi B+TREE ?
1. B+TREE est une variante de B TREE Les problèmes que B TREE peut résoudre, B+TREE peut également résoudre (réduire la hauteur de l'arbre et augmenter la quantité de données stockées dans. nœuds) 2. B+TREE a des capacités d'analyse de base de données et de table plus puissantes. Si nous voulons analyser la table de données en fonction de l'index, pour analyser B TREE, nous devons parcourir l'arbre entier, tandis que B+. TREE n'a qu'à le parcourir. Tous les nœuds feuilles sont suffisants (il y a des références entre les nœuds feuilles). 3. B+TREE a des capacités de lecture et d'écriture de disque plus fortes. Son nœud racine et ses nœuds de support n'enregistrent pas les zones de données. Lorsque tous les nœuds racine et les nœuds de support sont de la même taille, les mots-clés enregistrés sont plus grands que. ceux de B TREE. Vous en voulez plus. Les nœuds feuilles n'enregistrent pas les références aux nœuds enfants. Par conséquent, B+TREE lit et écrit plus de mots-clés chargés sur le disque que B TREE. 4. B+TREE a une capacité de tri plus forte. Comme le montre l'image ci-dessus, B+TREE a naturellement une fonction de tri. 5. L'efficacité des requêtes B+TREE est plus stable. Chaque fois que des données sont interrogées, le nombre de requêtes IO doit être stable. Bien sûr, la compréhension de chacun est différente, car dans B TREE, si le nœud racine frappe, il revient directement, ce qui est effectivement plus efficace.La forme spécifique d'implémentation de MYSQL B+TREE
L'explication principale ici est l'implémentation des deux moteurs de stockage de MYSQL (MYISAM et INNODB) basés sur différentes structures d'index B+TREE. Tout d'abord, recherchez le dossier dans lequel MYSQL enregistre les données et voyez comment MySQL enregistre les données :

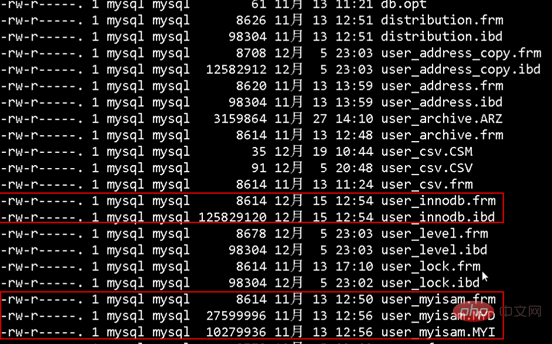
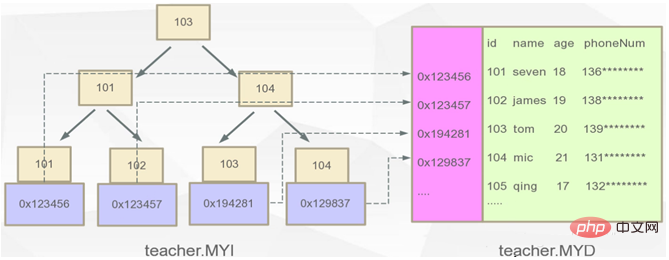
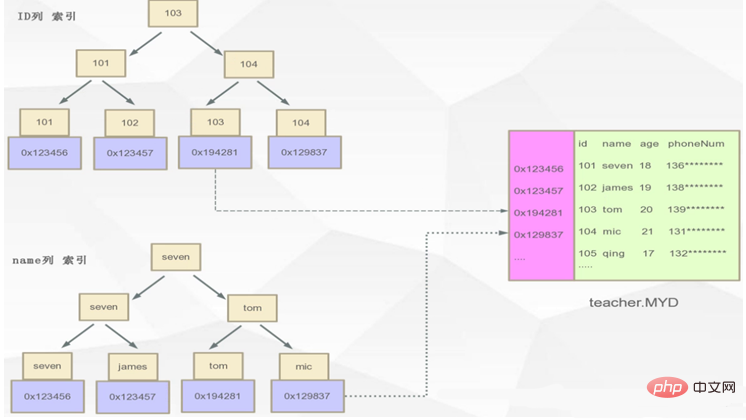
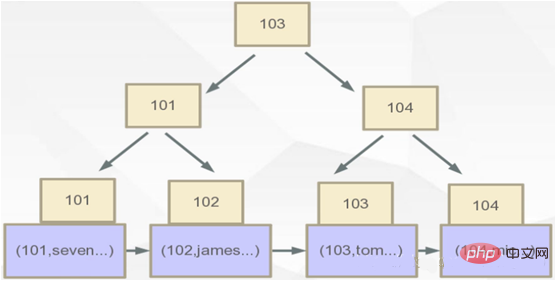
Dans innodb, le format de l'index auxiliaire est comme indiqué dans la figure ci-dessous ?
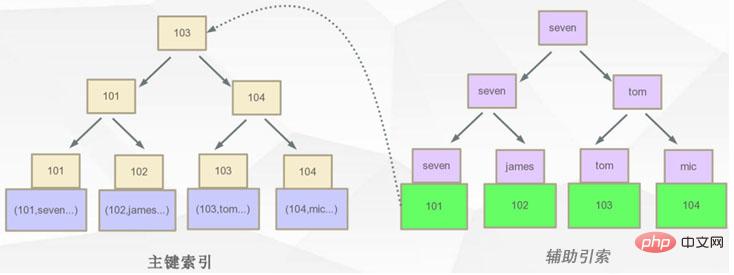
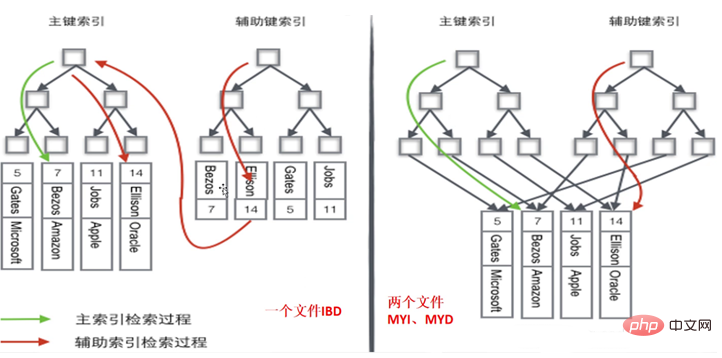
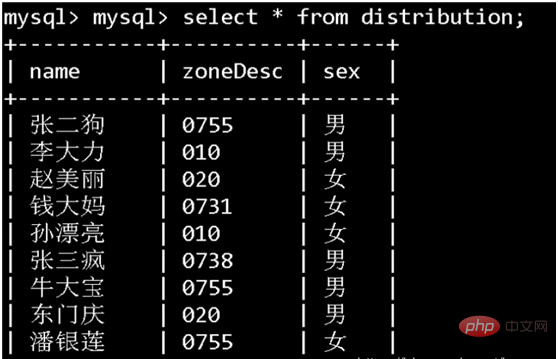
Pourquoi dit-on que plus le type discret est élevé, meilleur est le type sélectif ?
Comme indiqué ci-dessous, si vous créez un index pour le Sexe, la structure de l'index sera la suivante :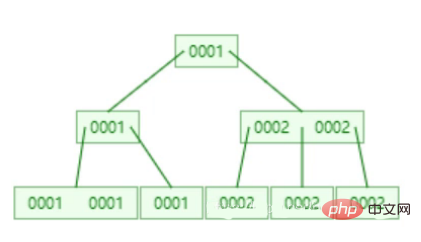
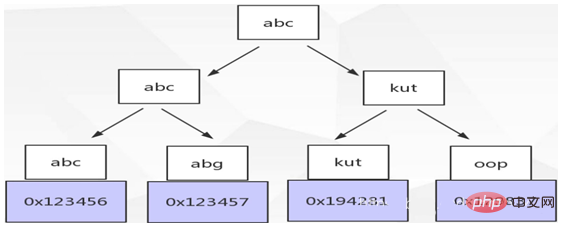
Lors de la correspondance, la chaîne sera convertie en code ascll, tel que abc devient 97 98 99, puis comparée caractère par caractère de gauche à droite. Par conséquent, lors de l'utilisation de %a dans une requête SQL, l'index sera invalide, car % signifie une correspondance complète, il n'est pas nécessaire d'avoir un index. Il est préférable d'analyser directement la table entière.
3. Principe du moindre espace
Comme mentionné précédemment, lorsque l'espace occupé par les mots-clés est plus petit, le nombre de mots-clés enregistrés dans chaque nœud sera plus important, qui seront chacun chargés dans la mémoire. plus il y a de mots-clés, plus l’efficacité de la recherche sera élevée.
Index syndical :
Index à colonne unique : mot-clé dans le nœud [nom]
Index syndical : mot-clé dans le nœud [nom, phoneNum]
Single- les index de colonnes peuvent être considérés comme des index conjoints spéciaux, et la comparaison des index conjoints est également basée sur le principe de correspondance le plus à gauche.
Principes de sélection des colonnes d'index conjoint :
(1) Priorité de colonne couramment utilisée (principe de correspondance le plus à gauche)
(2) Priorité de colonne à haute discrétion (principe discret de haute degré)
(3) Priorité de colonne de petite largeur, (principe du moindre espace)
Ce qui suit est un exemple simple de problèmes souvent rencontrés dans la vie quotidienne :
Par exemple, généralement la requête SQL fréquemment utilisée est la suivante :
Select * from users where name = ?
Select * from users where name = ? and pahoneNum = ?
Afin d'accélérer la récupération, créez un index pour l'interrogation SQL ci-dessus comme suit :
Create index idx_name on users(name)
Create index idx_name_phoneNum on users(name, phoneNum)
Dans la solution ci-dessus, selon le principe de correspondance le plus à gauche, idx_name est un index redondant, où name = ? peut également être récupéré à l'aide de l'index idx_name_phoneNum. Les index redondants augmenteront ou diminueront la consommation de performances pour maintenir l'équilibre B+TREE et occuperont de l'espace disque.
Index couvert :
Si la colonne interrogée peut être directement renvoyée via les informations de l'élément d'index, alors l'index est appelé index de couverture pour interroger SQL. La couverture des index peut améliorer l’efficacité des requêtes.
Ce qui suit explique l'indice de couverture à travers un exemple.
Table : enseignant
Index : PK(id), key(name, phoneNum), unique(teacherNo)
Lequel des SQL suivants utilise des index de couverture ?
Select teacherNo from teacher where teacherNo = ? : Lorsqu'elle est utilisée, lorsque TeacherNo est récupérée, la valeur TeacherNo dans l'index peut être directement renvoyée sans entrer dans la zone de données.
Select id,teacherNo from teacher where teacherNo = ? : Lorsqu'il est utilisé, le nœud feuille de l'index auxiliaire enregistre la valeur de l'index primaire, donc lorsque le nœud feuille de l'index auxiliaire est récupéré, l'identifiant peut être renvoyé.
Select name,phoneNum from teacher where teacherNo = ? : Non utilisé
Select phoneNum from teacher where name = ?, utilisé.
Après avoir connu l'index de couverture, vous saurez pourquoi il est nécessaire de ne pas utiliser select * dans SQL et de spécifier les champs spécifiques à interroger. L'une des raisons est que lors de l'utilisation de l'index de couverture, il n'est pas nécessaire. entrer Une fois dans la zone de données, les données peuvent être renvoyées directement, améliorant ainsi l'efficacité des requêtes.
Grâce à l'étude précédente, nous pouvons facilement comprendre les conclusions suivantes :
1. La longueur des données de la colonne d'index peut être aussi petite que possible si elle répond aux besoins de l'entreprise.
2. Plus il y a d'index dans le tableau, mieux c'est.
3. Dans la condition Where, comme 9%, comme %9%, comme%9, les trois méthodes n'utilisent pas l'index. Les deux dernières méthodes ne sont pas valides pour les index. Les premiers 9% sont incertains et dépendent du type discret de la colonne.En conclusion, ils peuvent être utilisés si la situation discrète s'avère particulièrement mauvaise, l'optimiseur de requêtes estime que les performances des requêtes d'index sont moins bonnes et ce n'est pas le cas. aussi bon qu'une analyse complète de la table.
4. Les index ne peuvent pas être utilisés pour NOT IN dans la condition Where
5. Utilisez les requêtes spécifiées plus souvent, renvoyez uniquement les colonnes souhaitées et utilisez select * less.
6. Si la fonction est utilisée dans la condition de requête, l'index sera invalide. Ceci est lié au type discret de la colonne. Une fois la fonction utilisée, la fonction est incertaine.
7. Dans l'index conjoint, si la recherche n'est pas lancée à partir de la colonne la plus à gauche de l'index, l'index ne peut pas être utilisé.
8. Pour faire correspondre l'index conjoint exactement à la colonne la plus à gauche et à la plage pour correspondre à une autre colonne, l'index peut être utilisé.
9. Dans l'index conjoint, si la requête a une requête de plage d'une certaine colonne, toutes les colonnes à droite de celle-ci ne peuvent pas utiliser l'index.
Tutoriel Mysql recommandé "Tutoriel Mysql "
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Article chaud

Outils chauds Tags

Article chaud

Tags d'article chaud

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Compétences de traitement de structures de données volumineuses de PHP
May 08, 2024 am 10:24 AM
Compétences de traitement de structures de données volumineuses de PHP
May 08, 2024 am 10:24 AM
Compétences de traitement de structures de données volumineuses de PHP
 Comment optimiser les performances des requêtes MySQL en PHP ?
Jun 03, 2024 pm 08:11 PM
Comment optimiser les performances des requêtes MySQL en PHP ?
Jun 03, 2024 pm 08:11 PM
Comment optimiser les performances des requêtes MySQL en PHP ?
 Comment utiliser la sauvegarde et la restauration MySQL en PHP ?
Jun 03, 2024 pm 12:19 PM
Comment utiliser la sauvegarde et la restauration MySQL en PHP ?
Jun 03, 2024 pm 12:19 PM
Comment utiliser la sauvegarde et la restauration MySQL en PHP ?
 Comment insérer des données dans une table MySQL en utilisant PHP ?
Jun 02, 2024 pm 02:26 PM
Comment insérer des données dans une table MySQL en utilisant PHP ?
Jun 02, 2024 pm 02:26 PM
Comment insérer des données dans une table MySQL en utilisant PHP ?
 Quels sont les scénarios d'application des types d'énumération Java dans les bases de données ?
May 05, 2024 am 09:06 AM
Quels sont les scénarios d'application des types d'énumération Java dans les bases de données ?
May 05, 2024 am 09:06 AM
Quels sont les scénarios d'application des types d'énumération Java dans les bases de données ?
 Comment corriger les erreurs mysql_native_password non chargé sur MySQL 8.4
Dec 09, 2024 am 11:42 AM
Comment corriger les erreurs mysql_native_password non chargé sur MySQL 8.4
Dec 09, 2024 am 11:42 AM
Comment corriger les erreurs mysql_native_password non chargé sur MySQL 8.4
 Comment utiliser les procédures stockées MySQL en PHP ?
Jun 02, 2024 pm 02:13 PM
Comment utiliser les procédures stockées MySQL en PHP ?
Jun 02, 2024 pm 02:13 PM
Comment utiliser les procédures stockées MySQL en PHP ?
 Stratégies d'optimisation des performances pour la pagination des tableaux PHP
May 02, 2024 am 09:27 AM
Stratégies d'optimisation des performances pour la pagination des tableaux PHP
May 02, 2024 am 09:27 AM
Stratégies d'optimisation des performances pour la pagination des tableaux PHP






