Qu'est-ce que cela signifie lorsqu'une fonction a deux zéros ?

Qu'est-ce que cela signifie qu'une fonction a deux zéros ?

Une fonction avec deux zéros a deux significations :

1. Le graphique de cette fonction a deux intersections avec l'axe des x.

2. Soit l'expression analytique de cette fonction égale à zéro et ayant deux points zéro.

Condition nécessaire : La fonction possède plusieurs points zéro et sa variable indépendante possède plusieurs puissances. Deux points zéro élevés à la puissance deux fois, plus de deux à la puissance deux fois.

Condition de détermination : Le point zéro est l'abscisse de l'intersection de l'image de la fonction et de l'axe des x, c'est-à-dire la valeur de x lorsque y=0. Il y a deux points zéro, c'est-à-dire qu'il y a deux points d'intersection entre l'image de la fonction et l'axe des x. Ils (c'est-à-dire les points d'intersection) sont (x1, 0) et (x2, 0), où x1 et x2. sont appelés points zéro. Plus de deux signifie qu’il y a plus de deux points d’intersection et que leurs points zéro sont x1, x2 et x3.

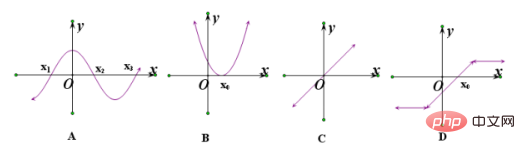
Informations étendues :

La valeur de la variable indépendante correspondante x lorsque f(x)=0 Il est à noter que le point zéro est un. valeur numérique, et Ce n'est pas un point, mais la coordonnée en abscisse de l'intersection de la fonction et de l'axe X.

Le point zéro de la fonction y=f(x) est la racine réelle de l'équation f(x)=0, qui est la direction transversale de l'intersection de l'image de la fonction y=f( x) et les coordonnées de l'axe des x (droite y=0), donc l'équation f(x)=0 a des racines réelles, le graphique de la fonction déduite y=f(x) a une intersection avec l'axe des x, et la fonction déduite y=f(x) a un point zéro.

Le point zéro du changement de signe est le point par lequel passe l'image de la fonction, c'est-à-dire que les valeurs des deux côtés de ce point ont des signes différents (la valeur de la fonction à ce point est zéro).

Le point zéro du signe invariant signifie que l'image de la fonction ne passe pas par ce point, c'est-à-dire que les valeurs des deux côtés de ce point ont le même signe (la valeur de la fonction à ce point est zéro).

Remarque : Si la valeur maximale de la fonction est 0, vous ne pouvez pas utiliser cette méthode pour trouver l'intervalle où se trouve le point zéro.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!