Utilisez des exemples de code Python pour démontrer l'application pratique de l'algorithme kNN_Connaissances de base

L'algorithme de classification du voisin le plus proche (kNN, k-NearestNeighbor) est l'une des méthodes les plus simples de la technologie de classification d'exploration de données. Le soi-disant K voisin le plus proche signifie k voisins les plus proches. Cela signifie que chaque échantillon peut être représenté par ses k voisins les plus proches.
L'idée centrale de l'algorithme kNN est que si la plupart des k échantillons adjacents les plus proches d'un échantillon dans l'espace des caractéristiques appartiennent à une certaine catégorie, alors l'échantillon appartient également à cette catégorie et possède les caractéristiques des échantillons de cette catégorie. Cette méthode détermine uniquement la catégorie de l'échantillon à classer sur la base de la catégorie du ou des échantillons les plus proches lors de la détermination de la décision de classification. La méthode kNN n'est pertinente que pour un très petit nombre d'échantillons adjacents lors de la prise de décisions de catégorie. Étant donné que la méthode kNN repose principalement sur les échantillons environnants limités plutôt que sur la méthode de discrimination du domaine de classe pour déterminer la catégorie, la méthode kNN est plus efficace que les autres méthodes pour diviser l'ensemble d'échantillons avec un grand nombre d'intersections ou de chevauchements dans le domaine de classe pour l'ajustement.

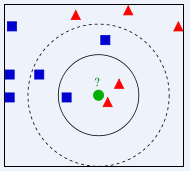
Dans l'image ci-dessus, à quelle classe doit être attribué le cercle vert ? Est-ce un triangle rouge ou un carré bleu ? Si K=3, puisque la proportion du triangle rouge est de 2/3, le cercle vert aura la classe du triangle rouge. Si K=5, puisque la proportion du carré bleu est de 3/5, le cercle vert. se verra attribuer la classe de type carré bleu.
L'algorithme de classification K-Nearest Neighbour (KNN) est une méthode théoriquement mature et l'un des algorithmes d'apprentissage automatique les plus simples. L'idée de cette méthode est la suivante : si un échantillon appartient à une certaine catégorie parmi les k échantillons les plus similaires (c'est-à-dire les plus proches dans l'espace des fonctionnalités) dans l'espace des fonctionnalités, alors l'échantillon appartient également à cette catégorie. Dans l'algorithme KNN, les voisins sélectionnés sont tous des objets correctement classés. Cette méthode détermine uniquement la catégorie de l'échantillon à classer en fonction de la catégorie du ou des échantillons les plus proches dans la prise de décision de classification. Bien que la méthode KNN repose également en principe sur le théorème limite, elle n’est liée qu’à un très petit nombre d’échantillons adjacents lors de la prise de décisions de catégorie. Étant donné que la méthode KNN repose principalement sur les échantillons environnants limités plutôt que sur la méthode de discrimination du domaine de classe pour déterminer la catégorie, la méthode KNN est plus efficace que les autres méthodes pour diviser l'ensemble d'échantillons avec un grand nombre d'intersections ou de chevauchements dans le domaine de classe pour l'ajustement.
L'algorithme KNN peut être utilisé non seulement pour la classification, mais aussi pour la régression. En trouvant les k voisins les plus proches d'un échantillon et en attribuant la moyenne des attributs de ces voisins à l'échantillon, les attributs de l'échantillon peuvent être obtenus. Une méthode plus utile consiste à attribuer des poids différents à l’influence des voisins situés à différentes distances sur l’échantillon. Par exemple, le poids est inversement proportionnel à la distance.

Utilisez l'algorithme kNN pour prédire le sexe des utilisateurs de films Douban
Résumé

Cet article estime que les types de films préférés par les personnes de sexes différents seront différents, c'est pourquoi cette expérience a été menée. Les 100 films récemment regardés par 274 utilisateurs actifs de Douban ont été utilisés pour établir des statistiques sur leurs types. Les 37 types de films obtenus ont été utilisés comme caractéristiques d'attribut et le sexe de l'utilisateur a été utilisé comme étiquette pour construire un ensemble d'échantillons. Utilisez l'algorithme kNN pour construire un classificateur de genre d'utilisateur de film Douban, en utilisant 90 % des échantillons comme échantillons d'apprentissage et 10 % comme échantillons de test, et la précision peut atteindre 81,48 %.

Données expérimentales

Les données utilisées dans cette expérience sont les films marqués par les utilisateurs de Douban, et les 100 films récemment regardés par 274 utilisateurs de Douban ont été sélectionnés. Statistiques des types de films pour chaque utilisateur. Il y a un total de 37 types de films dans les données utilisées dans cette expérience, donc ces 37 types sont utilisés comme caractéristiques d'attribut de l'utilisateur, et la valeur de chaque caractéristique est le nombre de films de ce type parmi les 100 films de l'utilisateur. Les utilisateurs sont étiquetés en fonction de leur sexe. Étant donné que Douban ne dispose pas d'informations sur le sexe des utilisateurs, tout est étiqueté manuellement.

Le format des données est le suivant :

X1,1，X1,2，X1,3，X1,4……X1,36，X1,37，Y1
X2,1，X2,2，X2,3，X2,4……X2,36，X2,37，Y2
…………
X274,1，X274,2，X274,3，X274,4……X274,36，X274,37，Y274

Exemple :

0,0,0,3,1,34,5,0,0,0,11,31,0,0,38,40,0,0,15,8,3,9,14,2,3,0,4,1,1,15,0,0,1,13,0,0,1,1 0,1,0,2,2,24,8,0,0,0,10,37,0,0,44,34,0,0,3,0,4,10,15,5,3,0,0,7,2,13,0,0,2,12,0,0,0,0

像这样的数据一共有274行，表示274个样本。每一个的前37个数据是该样本的37个特征值，最后一个数据为标签，即性别：0表示男性，1表示女性。

在此次试验中取样本的前10%作为测试样本，其余作为训练样本。

首先对所有数据归一化。对矩阵中的每一列求取最大值（max_j）、最小值（min_j)，对矩阵中的数据X_j，
X_j=(X_j-min_j)/(max_j-min_j) 。

然后对于每一条测试样本，计算其与所有训练样本的欧氏距离。测试样本i与训练样本j之间的距离为：
distance_i_j=sqrt((Xi,1-Xj,1)^2+(Xi,2-Xj,2)^2+……+(Xi,37-Xj,37)^2) ，
对样本i的所有距离从小到大排序，在前k个中选择出现次数最多的标签，即为样本i的预测值。

实验结果

首先选择一个合适的k值。 对于k=1,3,5,7，均使用同一个测试样本和训练样本，测试其正确率，结果如下表所示。

选取不同k值的正确率表

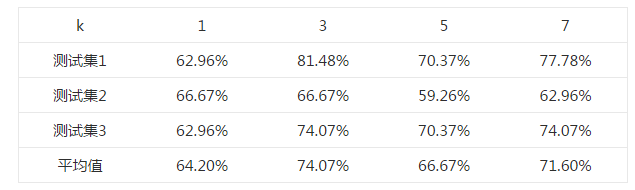
由上述结果可知，在k=3时，测试的平均正确率最高，为74.07%，最高可以达到81.48%。

上述不同的测试集均来自同一样本集中，为随机选取所得。

Python代码

这段代码并非原创，来自《机器学习实战》（Peter Harrington，2013），并有所改动。

#coding:utf-8

from numpy import *
import operator

def classify0(inX, dataSet, labels, k):
  dataSetSize = dataSet.shape[0]
  diffMat = tile(inX, (dataSetSize,1)) - dataSet
  sqDiffMat = diffMat**2
  sqDistances = sqDiffMat.sum(axis=1)
  distances = sqDistances**0.5
  sortedDistIndicies = distances.argsort()   
  classCount={}     
  for i in range(k):
    voteIlabel = labels[sortedDistIndicies[i]]
    classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
  sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
  return sortedClassCount[0][0]

def autoNorm(dataSet):
  minVals = dataSet.min(0)
  maxVals = dataSet.max(0)
  ranges = maxVals - minVals
  normDataSet = zeros(shape(dataSet))
  m = dataSet.shape[0]
  normDataSet = dataSet - tile(minVals, (m,1))
  normDataSet = normDataSet/tile(ranges, (m,1))  #element wise divide
  return normDataSet, ranges, minVals

def file2matrix(filename):
  fr = open(filename)
  numberOfLines = len(fr.readlines())     #get the number of lines in the file
  returnMat = zeros((numberOfLines,37))    #prepare matrix to return
  classLabelVector = []            #prepare labels return  
  fr = open(filename)
  index = 0
  for line in fr.readlines():
    line = line.strip()
    listFromLine = line.split(',')
    returnMat[index,:] = listFromLine[0:37]
    classLabelVector.append(int(listFromLine[-1]))
    index += 1
  fr.close()
  return returnMat,classLabelVector

def genderClassTest():
  hoRatio = 0.10   #hold out 10%
  datingDataMat,datingLabels = file2matrix('doubanMovieDataSet.txt')    #load data setfrom file
  normMat,ranges,minVals=autoNorm(datingDataMat)
  m = normMat.shape[0]
  numTestVecs = int(m*hoRatio)
  testMat=normMat[0:numTestVecs,:]
  trainMat=normMat[numTestVecs:m,:]
  trainLabels=datingLabels[numTestVecs:m]
  k=3
  errorCount = 0.0
  for i in range(numTestVecs):
    classifierResult = classify0(testMat[i,:],trainMat,trainLabels,k)
    print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
    if (classifierResult != datingLabels[i]):
      errorCount += 1.0
  print "Total errors:%d" %errorCount
  print "The total accuracy rate is %f" %(1.0-errorCount/float(numTestVecs))