Explication détaillée de la traversée en profondeur des arbres binaires en Java

Au cours des deux derniers jours, j'ai répondu à des questions d'algorithme liées aux arbres binaires et pris quelques notes d'étude. (Vous ne savez même pas comment créer des arbres binaires ? Vous n'êtes vraiment pas compétent et vous n'avez pas besoin d'écrire des algorithmes ou des structures de données liées aux arbres binaires dans votre travail quotidien. Parce que je suis bon dans ce domaine, je dois étudiez plus dur !)

Définition

Premier coup d'oeil à l'explication de Wikipédia : En informatique, un arbre binaire (anglais : Arbre binaire) est un arbre avec au plus deux branches par nœud (c'est-à-dire qu'il n'y a pas de structure arborescente avec un nœud avec un degré de branche supérieur à 2). Habituellement, les branches sont appelées « sous-arbre gauche » ou « sous-arbre droit ». Les branches d'un arbre binaire ont un ordre gauche et droit et ne peuvent pas être inversées à volonté.

En raison des caractéristiques définies par l'arbre binaire lui-même, il a un degré élevé de répétabilité locale. Par conséquent, lors de la traversée d'un arbre binaire en profondeur, il est généralement implémenté de manière récursive. cette façon est très concise et belle, et elle est plus facile à comprendre.

Parcours en profondeur d'abord

Généralement, nous avons trois parcours d'ordre les plus courants pour le parcours en profondeur d'abord des arbres binaires : pré-commande, en milieu de commande et après la commande.

L'ordre de parcours de la pré-commande est : visitez le nœud racine-> parcourez le sous-arbre de gauche-> parcourez le sous-arbre de droite

L'ordre de parcours de l'ordre intermédiaire est : parcourez le sous-arbre gauche-> ; Visitez le nœud racine-> Traversez le sous-arbre droit

L'ordre de parcours post-ordre est : Parcourez le sous-arbre gauche-> Parcourez le sous-arbre droit-> >

Remarque Les parties gauche et droite ici sont le sous-arbre entier, pas un nœud, car nous devons parcourir l'arbre entier, donc chaque parcours est effectué dans cet ordre jusqu'au nœud feuille.

Par exemple, s'il existe l'arbre binaire suivant :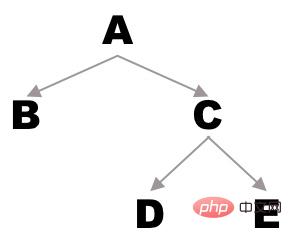

La séquence obtenue par parcours de pré-ordre est A - B - C - D - E

La séquence obtenue par parcours d'ordre intermédiaire est B - A - D - C - E

La séquence obtenue par parcours d'ordre post-ordre est B - D - E - C - A

Utilisons cette idée En terme de parcours de précommande (il est fortement déconseillé d'utiliser la récursion humaine, en tout cas mon cerveau ne supporte pas trois niveaux...) :

Récursion de premier niveau :

Visitez d'abord le nœud racine, donc sortez le nœud racine A, puis parcourez le sous-arbre gauche (L1), puis parcourez le sous-arbre droit (R1)

Récursivité de deuxième niveau :

 ; Pour L1, visitez d'abord le nœud racine, donc affichez le nœud racine B à ce moment, puis constatez que les sous-arbres gauche et droit de B sont vides et terminez la récursion

Pour R1, visitez la racine ; nœud d'abord, donc affichez le nœud racine C à ce moment, puis parcourez le sous-arbre gauche (L2), puis parcourez le sous-arbre droit (R2)

Récursion de troisième niveau :

Pour L2, le nœud racine est visité en premier, donc le nœud racine D est affiché à ce moment-là, puis constatez que les sous-arbres gauche et droit de D sont vides, terminez la récursion

Pour R2, visitez la racine ; nœud d'abord, donc affichez le nœud racine E à ce moment-là, puis constatez que les sous-arbres gauche et droit de E sont vides, terminez la récursion ;

Caractéristiques de l'ordre avant, intermédiaire et arrière

Selon la définition de l'ordre avant, milieu et arrière, il ne nous est en fait pas difficile de trouver les caractéristiques suivantes :

• Le premier du pré- order doit être le nœud racine, et le dernier de la post-commande doit être le nœud racine

• La distribution du sous-arbre gauche et du sous-arbre droit pour chaque tri est régulière

• Pour chaque sous-arbre suivant les deux règles ci-dessus, l'arbre

Ces caractéristiques sont l'expression de l'ordre dans la définition.

Diverses dérivations

Voici quelques-unes des questions algorithmiques les plus élémentaires pour la traversée d'un arbre binaire :

• Étant donné un binaire arbre, obtenez la séquence de son parcours pré/milieu/post-ordre ;

• Dérivation du post-ordre (ou dérivation de l'arbre binaire entier) basée sur le pré-ordre et le milieu d'ordre ; 🎜>

• Basé sur la post-commande et afin de déduire la pré-commande (ou de déduire l'arbre binaire entier)

Pour la traversée de l'arbre binaire, comme mentionné précédemment, la récursivité est généralement utilisée. Pour la récursivité, il existe un modèle qui peut être appliqué directement :

public void recur(int level, int param) {
    
    // terminator
    if (level > MAX_LEVEL) {
        // process result
         return;   
    }
    
    // process current logic
    process(level, param);
    
    // drill down
    recur(level+1, newParam);
    
    // restore current status
}

C'est une astuce plus pratique mentionnée par frère Chao (Qin Chao) dans le camp d'entraînement aux algorithmes que j'ai regardé ces deux derniers jours (ce modèle est particulièrement bon pour les novices). Suivez les trois étapes ci-dessus (si des variables locales sont nécessaires, une version ou un traitement supplémentaire sera effectué à l'étape 4). Vous pouvez écrire du code récursif de manière plus ordonnée.

Voici un exemple de dérivation de post-commande basée sur la précommande et la mi-commande :

initialisez d'abord les deux séquences :

int[] preSequence = {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] inSequence = {2, 3, 1, 6, 7, 8, 5, 9, 4};

Grâce aux plusieurs fonctionnalités mentionnées ci-dessus , nous avons Le sous-problème répété minimum peut être trouvé. Chaque récursion

correspond à l'indice i de la valeur du nœud dans l'ordre en fonction de la première valeur du nœud

de la séquence précédente, de sorte que Nous pouvons obtenir les parties avant et arrière de l'index i correspondant respectivement aux sous-arbres gauche et droit, puis parcourir respectivement les deux sous-arbres gauche et droit, puis afficher la première valeur de nœud du pré-ordre actuel, qui est le nœud racine.

Selon la méthode de programmation descendante, on peut d'abord écrire l'appel récursif initial suivant :

List<Integer> result = new ArrayList<>();
preAndInToPost(0, 0, preSequence.length, preSequence, inSequence, result);

Le premier paramètre représente le premier index d'élément de la séquence de précommande

<🎜 ; >Le deuxième paramètre représente l'indice du premier élément de la séquence dans l'ordre

Le troisième paramètre représente la longueur de la séquence

第四个参数表示前序序列；

第五个参数表示后序序列；

第六个参数用于保存结果；

先来考虑终止条件是什么，也就是什么时候结束递归，当我们的根结点为空的时候终止，对应这里就是序列长度为零的时候。

if (length == 0) {
    return;
}

接着考虑处理逻辑，也就是找到索引 i：

int i = 0;
while (inSequence[inIndex + i] != preSequence[preIndex]) {
    i++;
}

然后开始向下递归：

preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
result.add(preSequence[preIndex]);

因为推导的是后序序列，所以顺序如上，添加根结点的操作是在最后的。前三个参数如何得出来的呢，我们走一下第一次遍历就可以得出来。

前序序列的第一个结点 1 在中序序列中的索引为 2，此时

左子树的中序系列起始索引为总序列的第 1 个索引，长度为 2；

左子树的前序序列起始索引为总序列的第 2 个索引，长度为 2；

右子树的中序系列起始索引为总序列的第 3 个索引，长度为 length - 3；

右子树的前序序列起始索引为总序列的第 3 个索引，长度为 length - 3；

完整代码如下：

/**
 * 根据前序和中序推导后序
 *
 * @param preIndex    前序索引
 * @param inIndex     中序索引
 * @param length      序列长度
 * @param preSequence 前序序列
 * @param inSequence  中序序列
 * @param result      结果序列
 */
private void preAndInToPost(int preIndex, int inIndex, int length, int[] preSequence, int[] inSequence, List<Integer> result) {
    if (length == 0) {
        return;
    }

    int i = 0;
    while (inSequence[inIndex + i] != preSequence[preIndex]) {
        i++;
    }

    preAndInToPost(preIndex + 1, inIndex, i, preSequence, inSequence, result);
    preAndInToPost(preIndex + i + 1, inIndex + i + 1, length - i - 1, preSequence, inSequence, result);
    result.add(preSequence[preIndex]);
}

参考链接

• 维基百科 - 二叉树（https://zh.wikipedia.org/wiki/%E4%BA%8C%E5%8F%89%E6%A0%91）

推荐教程：《java教程》

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!