 interface Web
interface Web
 js tutoriel
js tutoriel
 Comment créer et parcourir un arbre binaire en javascript ? (exemple de code)
Comment créer et parcourir un arbre binaire en javascript ? (exemple de code)
Comment créer et parcourir un arbre binaire en javascript ? (exemple de code)

Cet article vous présentera comment créer et parcourir un arbre binaire à l'aide de JavaScript. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer. J'espère qu'il sera utile à tout le monde.
1. Parlons d'abord de la traversée d'arbre binaire. La méthode de traversée :
Parcours de pré-commande : parcourez d'abord le nœud racine, puis le sous-arbre gauche. , puis le sous-arbre droit.
Parcours dans l'ordre : parcourez d'abord le sous-arbre gauche, puis le nœud racine, puis le sous-arbre droit
Parcours suivant : parcourez d'abord le sous-arbre gauche, puis le sous-arbre droit, puis le nœud racine
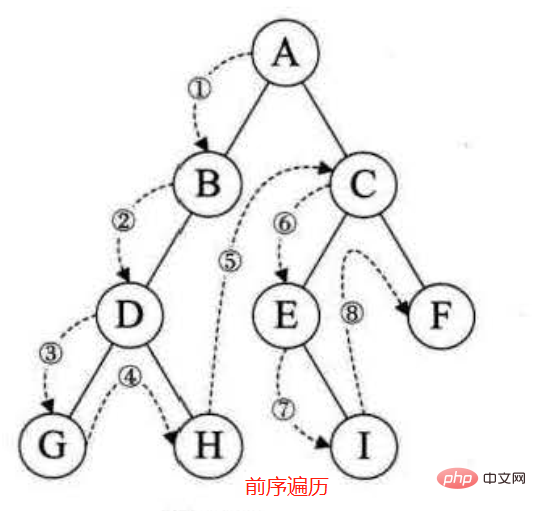
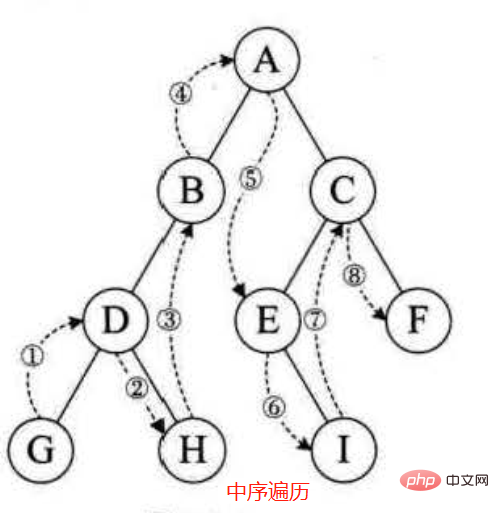
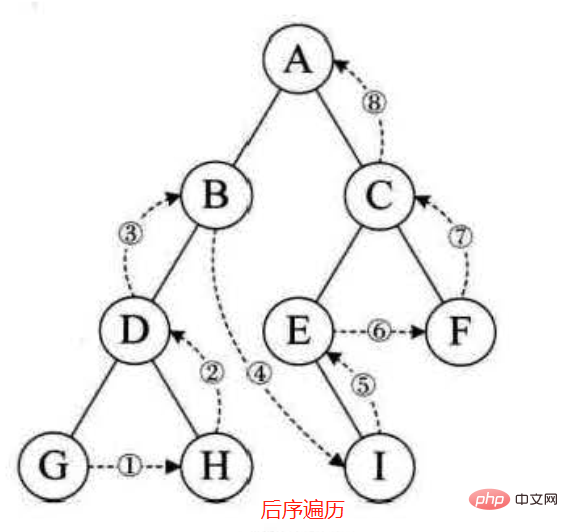
Le code ci-dessus : utilise principalement la récursion
function TreeCode() {
let BiTree = function (ele) {
this.data = ele;
this.lChild = null;
this.rChild = null;
}
this.createTree = function () {
let biTree = new BiTree('A');
biTree.lChild = new BiTree('B');
biTree.rChild = new BiTree('C');
biTree.lChild.lChild = new BiTree('D');
biTree.lChild.lChild.lChild = new BiTree('G');
biTree.lChild.lChild.rChild = new BiTree('H');
biTree.rChild.lChild = new BiTree('E');
biTree.rChild.rChild = new BiTree('F');
biTree.rChild.lChild.rChild = new BiTree('I');
return biTree;
}
}
//前序遍历
function ProOrderTraverse(biTree) {
if (biTree == null) return;
console.log(biTree.data);
ProOrderTraverse(biTree.lChild);
ProOrderTraverse(biTree.rChild);
}
//中序遍历
function InOrderTraverse(biTree) {
if (biTree == null) return;
InOrderTraverse(biTree.lChild);
console.log(biTree.data);
InOrderTraverse(biTree.rChild);
}
//后续遍历
function PostOrderTraverse(biTree) {
if (biTree == null) return;
PostOrderTraverse(biTree.lChild);
PostOrderTraverse(biTree.rChild);
console.log(biTree.data);
}
let myTree = new TreeCode();
console.log(myTree.createTree());
console.log('前序遍历')
ProOrderTraverse(myTree.createTree());
console.log('中序遍历')
InOrderTraverse(myTree.createTree());
console.log('后续遍历')
PostOrderTraverse(myTree.createTree());Parcours non récursif d'arbres binaires
Parcours en profondeur d'abord (principalement en utilisant le premier entré-dernier sorti de la pile)
Parcours en largeur d'abord (en utilisant principalement le premier entré, premier sorti de la file d'attente)
//深度优先非递归
function DepthFirstSearch(biTree) {
let stack = [];
stack.push(biTree);
while (stack.length != 0) {
let node = stack.pop();
console.log(node.data);
if (node.rChild) {
stack.push(node.rChild);
}
if (node.lChild) {
stack.push(node.lChild);
}
}
}
//广度优先非递归
function BreadthFirstSearch(biTree) {
let queue = [];
queue.push(biTree);
while (queue.length != 0) {
let node = queue.shift();
console.log(node.data);
if (node.lChild) {
queue.push(node.lChild);
}
if (node.rChild) {
queue.push(node.rChild);
}
}
}La priorité de profondeur utilise principalement la pile, en appuyant d'abord sur le sous-arbre droit, puis sur le sous-arbre gauche
Priorité de largeur utilise principalement la file d'attente, entrant d'abord dans le sous-arbre de gauche, puis dans le sous-arbre de droite
Priorité en profondeur Le résultat du parcours est le même que le parcours de pré-ordre ABDGHCEIF, et le résultat du parcours en largeur en premier est ABCDEFGHI
2. Créer un arbre binaire
La façon de créer un arbre binaire en 1 est trop maladroite, et elle est fausse pour nous Construisez votre propre arbre binaire basé sur l'arbre binaire complet modèle. Les données vides sont représentées par #. Comme le montre la figure ci-dessous, nous l'appelons un arbre binaire étendu. Nous prenons la séquence AB#D##C## du parcours de pré-ordre.

Le code ci-dessus : utilise également la récursion
//前序遍历得到的字符串
let strArr = 'AB#D##C##'.split('');
function BiTree(ele) {
this.data = ele;
this.lChild = null;
this.rChild = null;
}
var newTree = new BiTree('#');
function createBiTree(biTree) {
if (strArr.length == 0) return;
let str = strArr.shift();
if (str == '#') return;
biTree.data = str;
if (strArr[0] != '#') {
biTree.lChild = new BiTree('#')
}
createBiTree(biTree.lChild);
if (strArr[0] != '#') {
biTree.rChild = new BiTree('#')
}
createBiTree(biTree.rChild);
}
createBiTree(newTree);
console.log(newTree);
ProOrderTraverse(newTree)Vous pouvez également utiliser le parcours dans l'ordre ou le parcours post-ordre pour créer un arbre binaire Le code. génère un nœud et échange simplement l'ordre des codes pour construire les sous-arbres gauche et droit
Tutoriel recommandé : "Tutoriel vidéo JavaScript"
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment mettre en œuvre un système de reconnaissance vocale en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 pm 02:54 PM
Comment mettre en œuvre un système de reconnaissance vocale en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 pm 02:54 PM
Comment utiliser WebSocket et JavaScript pour mettre en œuvre un système de reconnaissance vocale en ligne Introduction : Avec le développement continu de la technologie, la technologie de reconnaissance vocale est devenue une partie importante du domaine de l'intelligence artificielle. Le système de reconnaissance vocale en ligne basé sur WebSocket et JavaScript présente les caractéristiques d'une faible latence, d'un temps réel et d'une multiplateforme, et est devenu une solution largement utilisée. Cet article explique comment utiliser WebSocket et JavaScript pour implémenter un système de reconnaissance vocale en ligne.
 WebSocket et JavaScript : technologies clés pour mettre en œuvre des systèmes de surveillance en temps réel
Dec 17, 2023 pm 05:30 PM
WebSocket et JavaScript : technologies clés pour mettre en œuvre des systèmes de surveillance en temps réel
Dec 17, 2023 pm 05:30 PM
WebSocket et JavaScript : technologies clés pour réaliser des systèmes de surveillance en temps réel Introduction : Avec le développement rapide de la technologie Internet, les systèmes de surveillance en temps réel ont été largement utilisés dans divers domaines. L'une des technologies clés pour réaliser une surveillance en temps réel est la combinaison de WebSocket et de JavaScript. Cet article présentera l'application de WebSocket et JavaScript dans les systèmes de surveillance en temps réel, donnera des exemples de code et expliquera leurs principes de mise en œuvre en détail. 1. Technologie WebSocket
 Comment utiliser JavaScript et WebSocket pour mettre en œuvre un système de commande en ligne en temps réel
Dec 17, 2023 pm 12:09 PM
Comment utiliser JavaScript et WebSocket pour mettre en œuvre un système de commande en ligne en temps réel
Dec 17, 2023 pm 12:09 PM
Introduction à l'utilisation de JavaScript et de WebSocket pour mettre en œuvre un système de commande en ligne en temps réel : avec la popularité d'Internet et les progrès de la technologie, de plus en plus de restaurants ont commencé à proposer des services de commande en ligne. Afin de mettre en œuvre un système de commande en ligne en temps réel, nous pouvons utiliser les technologies JavaScript et WebSocket. WebSocket est un protocole de communication full-duplex basé sur le protocole TCP, qui peut réaliser une communication bidirectionnelle en temps réel entre le client et le serveur. Dans le système de commande en ligne en temps réel, lorsque l'utilisateur sélectionne des plats et passe une commande
 Comment mettre en œuvre un système de réservation en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 am 09:39 AM
Comment mettre en œuvre un système de réservation en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 am 09:39 AM
Comment utiliser WebSocket et JavaScript pour mettre en œuvre un système de réservation en ligne. À l'ère numérique d'aujourd'hui, de plus en plus d'entreprises et de services doivent fournir des fonctions de réservation en ligne. Il est crucial de mettre en place un système de réservation en ligne efficace et en temps réel. Cet article explique comment utiliser WebSocket et JavaScript pour implémenter un système de réservation en ligne et fournit des exemples de code spécifiques. 1. Qu'est-ce que WebSocket ? WebSocket est une méthode full-duplex sur une seule connexion TCP.
 JavaScript et WebSocket : créer un système efficace de prévisions météorologiques en temps réel
Dec 17, 2023 pm 05:13 PM
JavaScript et WebSocket : créer un système efficace de prévisions météorologiques en temps réel
Dec 17, 2023 pm 05:13 PM
JavaScript et WebSocket : Construire un système efficace de prévisions météorologiques en temps réel Introduction : Aujourd'hui, la précision des prévisions météorologiques revêt une grande importance pour la vie quotidienne et la prise de décision. À mesure que la technologie évolue, nous pouvons fournir des prévisions météorologiques plus précises et plus fiables en obtenant des données météorologiques en temps réel. Dans cet article, nous apprendrons comment utiliser la technologie JavaScript et WebSocket pour créer un système efficace de prévisions météorologiques en temps réel. Cet article démontrera le processus de mise en œuvre à travers des exemples de code spécifiques. Nous
 Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript : Comment obtenir le code d'état HTTP, des exemples de code spécifiques sont requis Préface : Dans le développement Web, l'interaction des données avec le serveur est souvent impliquée. Lors de la communication avec le serveur, nous devons souvent obtenir le code d'état HTTP renvoyé pour déterminer si l'opération a réussi et effectuer le traitement correspondant en fonction de différents codes d'état. Cet article vous apprendra comment utiliser JavaScript pour obtenir des codes d'état HTTP et fournira quelques exemples de codes pratiques. Utilisation de XMLHttpRequest
 Comment utiliser insertBefore en javascript
Nov 24, 2023 am 11:56 AM
Comment utiliser insertBefore en javascript
Nov 24, 2023 am 11:56 AM
Utilisation : En JavaScript, la méthode insertBefore() est utilisée pour insérer un nouveau nœud dans l'arborescence DOM. Cette méthode nécessite deux paramètres : le nouveau nœud à insérer et le nœud de référence (c'est-à-dire le nœud où le nouveau nœud sera inséré).
 Comment obtenir facilement le code d'état HTTP en JavaScript
Jan 05, 2024 pm 01:37 PM
Comment obtenir facilement le code d'état HTTP en JavaScript
Jan 05, 2024 pm 01:37 PM
Introduction à la méthode d'obtention du code d'état HTTP en JavaScript : Dans le développement front-end, nous devons souvent gérer l'interaction avec l'interface back-end, et le code d'état HTTP en est une partie très importante. Comprendre et obtenir les codes d'état HTTP nous aide à mieux gérer les données renvoyées par l'interface. Cet article explique comment utiliser JavaScript pour obtenir des codes d'état HTTP et fournit des exemples de code spécifiques. 1. Qu'est-ce que le code d'état HTTP ? Le code d'état HTTP signifie que lorsque le navigateur lance une requête au serveur, le service





