

L'une des structures de données les plus couramment utilisées et discutées en informatique est l'arbre de recherche binaire. Il s'agit généralement de la première structure de données introduite avec un algorithme d'insertion non linéaire. Les arbres de recherche binaires sont similaires aux listes doublement chaînées, chaque nœud contient des données et deux pointeurs vers d'autres nœuds. Ils diffèrent par la manière dont ces nœuds sont liés les uns aux autres ; Les pointeurs vers les nœuds de l'arbre de recherche binaire sont souvent appelés « gauche » et « droite » et sont utilisés pour indiquer le sous-arbre associé à la valeur actuelle. Une implémentation JavaScript simple d'un tel nœud est la suivante :
var node = {
value: 125,
left: null,
right: null
};Comme son nom l'indique, un arbre de recherche binaire est organisé en une structure hiérarchique en forme d'arbre. Le premier élément devient le nœud racine et chaque valeur supplémentaire est ajoutée à l'arborescence en tant qu'ancêtre de cette racine. Cependant, les valeurs sur les nœuds d'un arbre de recherche binaire sont uniques et ordonnées selon la valeur qu'elles contiennent : comme les valeurs dans le sous-arbre gauche d'un nœud sont toujours plus petites que la valeur du nœud, les valeurs dans le sous-arbre de droite est toujours plus grand que la valeur du nœud. De cette façon, trouver des valeurs dans un arbre de recherche binaire devient très simple, tant que la valeur que vous recherchez est plus petite que le nœud sur lequel vous travaillez alors déplacez-vous vers la gauche, si la valeur est plus grande alors déplacez-vous vers la droite. Il ne peut pas y avoir de doublons dans un arbre de recherche binaire car la duplication rompt la relation. La figure ci-dessous représente un simple arbre de recherche binaire.
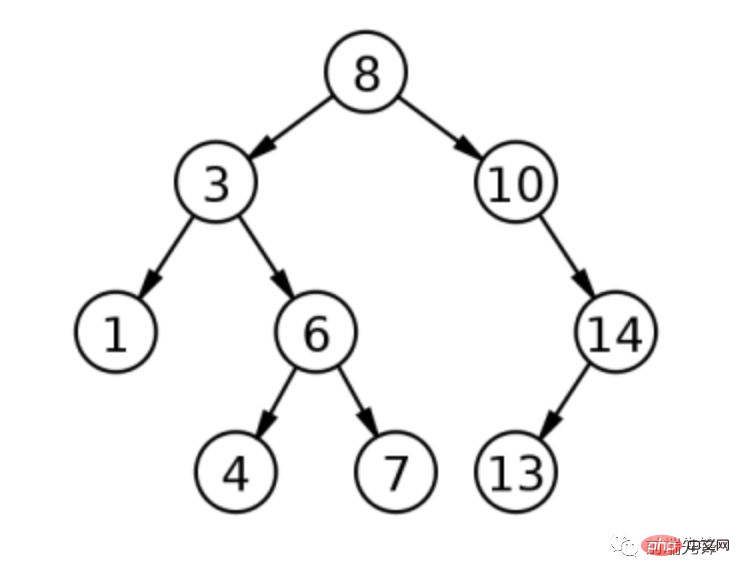
La figure ci-dessus représente un arbre de recherche binaire avec une valeur racine de 8. Lorsque la valeur 3 est ajoutée, elle devient l'enfant gauche de la racine car 3 est inférieur à 8. Lorsque la valeur 1 est ajoutée, elle devient l'enfant gauche de 3 car 1 est inférieur à 8 (donc à gauche) puis 1 est inférieur à 3 (encore une fois à gauche). Lorsque la valeur 10 est ajoutée, elle devient le bon enfant de follow car 10 est supérieur à 8. Continuez ce processus avec les valeurs 6, 4, 7, 14 et 13. La profondeur de cet arbre de recherche binaire est de 3, ce qui signifie que le nœud le plus éloigné de la racine est composé de trois nœuds.
Les arbres de recherche binaires se retrouvent dans un ordre naturellement trié, ils peuvent donc être utilisés pour trouver des données rapidement car vous pouvez éliminer instantanément les possibilités pour chaque étape. Les recherches peuvent être effectuées plus rapidement en limitant le nombre de nœuds à trouver. Supposons que vous souhaitiez trouver la valeur 6 dans l’arborescence ci-dessus. En partant de la racine, on détermine que 6 est inférieur à 8, on passe donc au fils gauche de la racine. Puisque 6 est supérieur à 3, vous irez au bon nœud. Vous pouvez trouver la valeur correcte. Il vous suffit donc de visiter trois nœuds au lieu de neuf pour trouver cette valeur.
Pour implémenter un arbre de recherche binaire en JavaScript, la première étape consiste à définir une interface de base :
function BinarySearchTree() {
this._root = null;
}
BinarySearchTree.prototype = {
//restore constructor
constructor: BinarySearchTree,
add: function (value){
},
contains: function(value){
},
remove: function(value){
},
size: function(){
},
toArray: function(){
},
toString: function(){
}
};L'interface de base est similaire aux autres structures de données, avec des méthodes d'ajout et de suppression de valeurs. J'ai également ajouté quelques méthodes pratiques, size(), toArray() et toString(), qui sont utiles pour JavaScript.
Pour maîtriser l'utilisation des arbres de recherche binaires, il est préférable de commencer par la méthode contains(). La méthode contains() accepte une valeur comme argument et renvoie true si la valeur existe dans l'arborescence, sinon elle renvoie false. Cette méthode suit un algorithme de recherche binaire de base pour déterminer si la valeur existe :
BinarySearchTree.prototype = {
//more code
contains: function(value){
var found = false,
current = this._root
//make sure there's a node to search
while(!found && current){
//if the value is less than the current node's, go left
if (value < current.value){
current = current.left;
//if the value is greater than the current node's, go right
} else if (value > current.value){
current = current.right;
//values are equal, found it!
} else {
found = true;
}
}
//only proceed if the node was found
return found;
},
//more code
};La recherche commence à la racine de l'arbre. Si aucune donnée n’est ajoutée, alors il n’y a probablement pas de racine, vous devez donc vérifier. Le parcours de l'arborescence suit l'algorithme simple évoqué précédemment : déplacez-vous vers la gauche si la valeur que vous recherchez est plus petite que le nœud actuel, et déplacez-vous vers la droite si la valeur est plus grande. Le pointeur current est écrasé à chaque fois jusqu'à ce que la valeur qu'il recherche soit trouvée (auquel cas found est défini sur true) ou qu'il n'y ait plus de nœuds dans cette direction (auquel cas la valeur n'est pas sur arbres).
Les méthodes utilisées dans contains() peuvent également être utilisées pour insérer de nouvelles valeurs dans l'arborescence. La principale différence est que vous cherchez où mettre la nouvelle valeur, plutôt que de chercher la valeur dans l'arbre :
BinarySearchTree.prototype = {
//more code
add: function(value){
//create a new item object, place data in
var node = {
value: value,
left: null,
right: null
},
//used to traverse the structure
current;
//special case: no items in the tree yet
if (this._root === null){
this._root = node;
} else {
current = this._root;
while(true){
//if the new value is less than this node's value, go left
if (value < current.value){
//if there's no left, then the new node belongs there
if (current.left === null){
current.left = node;
break;
} else {
current = current.left;
}
//if the new value is greater than this node's value, go right
} else if (value > current.value){
//if there's no right, then the new node belongs there
if (current.right === null){
current.right = node;
break;
} else {
current = current.right;
}
//if the new value is equal to the current one, just ignore
} else {
break;
}
}
}
},
//more code
}; Le cas particulier lors de l'ajout d'une valeur dans un arbre de recherche binaire est lorsqu'il n'y a pas racine. Dans ce cas, il suffit de définir la racine sur une nouvelle valeur pour faire le travail facilement. Pour les autres cas, l'algorithme de base est exactement le même que celui utilisé dans contains() : allez à gauche si la nouvelle valeur est plus petite que le nœud actuel, et allez à droite si la valeur est plus grande. La principale différence est que c'est là que se trouve la nouvelle valeur lorsque vous ne pouvez pas aller plus loin. Donc, si vous devez vous déplacer vers la gauche mais qu'il n'y a pas de nœud gauche, la nouvelle valeur sera le nœud gauche (identique au nœud droit). Puisqu'il n'y a pas de doublons, l'opération s'arrête si un nœud avec la même valeur est trouvé.
在继续讨论 size() 方法之前,我想深入讨论树遍历。为了计算二叉搜索树的大小,必须要访问树中的每个节点。二叉搜索树通常会有不同类型的遍历方法,最常用的是有序遍历。通过处理左子树,然后是节点本身,然后是右子树,在每个节点上执行有序遍历。由于二叉搜索树以这种方式排序,从左到右,结果是节点以正确的排序顺序处理。对于 size() 方法,节点遍历的顺序实际上并不重要,但它对 toArray() 方法很重要。由于两种方法都需要执行遍历,我决定添加一个可以通用的 traverse() 方法:
BinarySearchTree.prototype = {
//more code
traverse: function(process){
//helper function
function inOrder(node){
if (node){
//traverse the left subtree
if (node.left !== null){
inOrder(node.left);
}
//call the process method on this node
process.call(this, node);
//traverse the right subtree
if (node.right !== null){
inOrder(node.right);
}
}
}
//start with the root
inOrder(this._root);
},
//more code
};此方法接受一个参数 process,这是一个应该在树中的每个节点上运行的函数。该方法定义了一个名为 inOrder() 的辅助函数用于递归遍历树。注意,如果当前节点存在,则递归仅左右移动(以避免多次处理 null )。然后 traverse() 方法从根节点开始按顺序遍历,process() 函数处理每个节点。然后可以使用此方法实现size()、toArray()、toString():
BinarySearchTree.prototype = {
//more code
size: function(){
var length = 0;
this.traverse(function(node){
length++;
});
return length;
},
toArray: function(){
var result = [];
this.traverse(function(node){
result.push(node.value);
});
return result;
},
toString: function(){
return this.toArray().toString();
},
//more code
};size() 和 toArray() 都调用 traverse() 方法并传入一个函数来在每个节点上运行。在使用 size()的情况下,函数只是递增长度变量,而 toArray() 使用函数将节点的值添加到数组中。 toString()方法在调用 toArray() 之前把返回的数组转换为字符串,并返回 。
删除节点时,你需要确定它是否为根节点。根节点的处理方式与其他节点类似,但明显的例外是根节点需要在结尾处设置为不同的值。为简单起见,这将被视为 JavaScript 代码中的一个特例。
删除节点的第一步是确定节点是否存在:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//make sure there's a node to search
while(!found && current){
//if the value is less than the current node's, go left
if (value < current.value){
parent = current;
current = current.left;
//if the value is greater than the current node's, go right
} else if (value > current.value){
parent = current;
current = current.right;
//values are equal, found it!
} else {
found = true;
}
}
//only proceed if the node was found
if (found){
//continue
}
},
//more code here
};remove()方法的第一部分是用二叉搜索定位要被删除的节点,如果值小于当前节点的话则向左移动,如果值大于当前节点则向右移动。当遍历时还会跟踪 parent 节点,因为你最终需要从其父节点中删除该节点。当 found 等于 true 时,current 的值是要删除的节点。
删除节点时需要注意三个条件:
1、叶子节点
2、只有一个孩子的节点
3、有两个孩子的节点
从二叉搜索树中删除除了叶节点之外的内容意味着必须移动值来对树正确的排序。前两个实现起来相对简单,只删除了一个叶子节点,删除了一个带有一个子节点的节点并用其子节点替换。最后一种情况有点复杂,以便稍后访问。
在了解如何删除节点之前,你需要知道节点上究竟存在多少个子节点。一旦知道了,你必须确定节点是否为根节点,留下一个相当简单的决策树:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//find the node (removed for space)
//only proceed if the node was found
if (found){
//figure out how many children
childCount = (current.left !== null ? 1 : 0) +
(current.right !== null ? 1 : 0);
//special case: the value is at the root
if (current === this._root){
switch(childCount){
//no children, just erase the root
case 0:
this._root = null;
break;
//one child, use one as the root
case 1:
this._root = (current.right === null ?
current.left : current.right);
break;
//two children, little work to do
case 2:
//TODO
//no default
}
//non-root values
} else {
switch (childCount){
//no children, just remove it from the parent
case 0:
//if the current value is less than its
//parent's, null out the left pointer
if (current.value < parent.value){
parent.left = null;
//if the current value is greater than its
//parent's, null out the right pointer
} else {
parent.right = null;
}
break;
//one child, just reassign to parent
case 1:
//if the current value is less than its
//parent's, reset the left pointer
if (current.value < parent.value){
parent.left = (current.left === null ?
current.right : current.left);
//if the current value is greater than its
//parent's, reset the right pointer
} else {
parent.right = (current.left === null ?
current.right : current.left);
}
break;
//two children, a bit more complicated
case 2:
//TODO
//no default
}
}
}
},
//more code here
};处理根节点时,这是一个覆盖它的简单过程。对于非根节点,必须根据要删除的节点的值设置 parent 上的相应指针:如果删除的值小于父节点,则 left 指针必须重置为 null (对于没有子节点的节点)或删除节点的 left 指针;如果删除的值大于父级,则必须将 right 指针重置为 null 或删除的节点的 right指针。
如前所述,删除具有两个子节点的节点是最复杂的操作。考虑二元搜索树的以下表示。
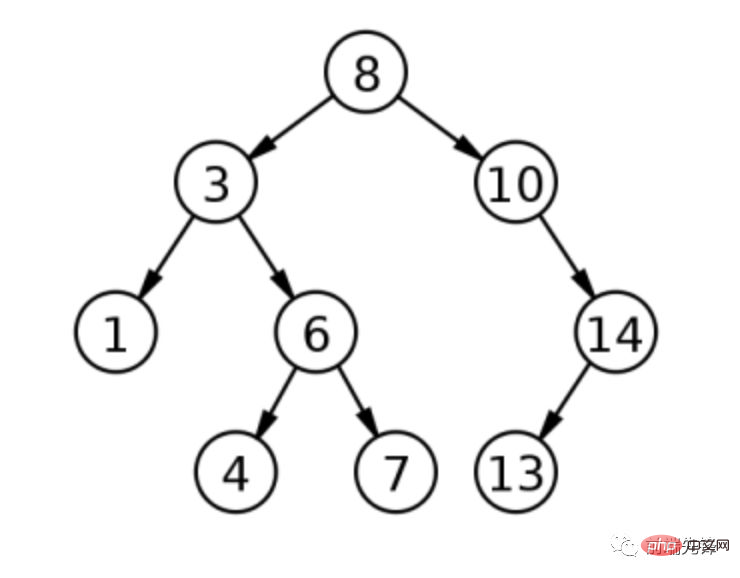
根为 8,左子为 3,如果 3 被删除会发生什么?有两种可能性:1(3 左边的孩子,称为有序前身)或4(右子树的最左边的孩子,称为有序继承者)都可以取代 3。
这两个选项中的任何一个都是合适的。要查找有序前驱,即删除值之前的值,请检查要删除的节点的左子树,并选择最右侧的子节点;找到有序后继,在删除值后立即出现的值,反转进程并检查最左侧的右子树。其中每个都需要另一次遍历树来完成操作:
BinarySearchTree.prototype = {
//more code here
remove: function(value){
var found = false,
parent = null,
current = this._root,
childCount,
replacement,
replacementParent;
//find the node (removed for space)
//only proceed if the node was found
if (found){
//figure out how many children
childCount = (current.left !== null ? 1 : 0) +
(current.right !== null ? 1 : 0);
//special case: the value is at the root
if (current === this._root){
switch(childCount){
//other cases removed to save space
//two children, little work to do
case 2:
//new root will be the old root's left child
//...maybe
replacement = this._root.left;
//find the right-most leaf node to be
//the real new root
while (replacement.right !== null){
replacementParent = replacement;
replacement = replacement.right;
}
//it's not the first node on the left
if (replacementParent !== null){
//remove the new root from it's
//previous position
replacementParent.right = replacement.left;
//give the new root all of the old
//root's children
replacement.right = this._root.right;
replacement.left = this._root.left;
} else {
//just assign the children
replacement.right = this._root.right;
}
//officially assign new root
this._root = replacement;
//no default
}
//non-root values
} else {
switch (childCount){
//other cases removed to save space
//two children, a bit more complicated
case 2:
//reset pointers for new traversal
replacement = current.left;
replacementParent = current;
//find the right-most node
while(replacement.right !== null){
replacementParent = replacement;
replacement = replacement.right;
}
replacementParent.right = replacement.left;
//assign children to the replacement
replacement.right = current.right;
replacement.left = current.left;
//place the replacement in the right spot
if (current.value < parent.value){
parent.left = replacement;
} else {
parent.right = replacement;
}
//no default
}
}
}
},
//more code here
};具有两个子节点的根节点和非根节点的代码几乎相同。此实现始终通过查看左子树并查找最右侧子节点来查找有序前驱。遍历是使用 while 循环中的 replacement 和 replacementParent 变量完成的。
replacement中的节点最终成为替换 current 的节点,因此通过将其父级的 right 指针设置为替换的 left 指针,将其从当前位置移除。
Pour le nœud racine, lorsque replacement est un enfant direct du nœud racine, replacementParent sera null, donc le pointeur replacement de right est simplement défini sur le pointeur right de la racine.
La dernière étape consiste à attribuer le nœud de remplacement au bon emplacement. Pour les nœuds racines, le remplacement est défini sur la nouvelle racine ; pour les nœuds non racines, le remplacement est attribué à la position appropriée sur le parent d'origine.
Remarque sur cette implémentation : toujours remplacer les nœuds par des prédécesseurs ordonnés peut entraîner un arbre déséquilibré, où la plupart des valeurs seront d'un côté de l'arbre. Un arbre déséquilibré signifie une recherche moins efficace et devrait donc être un sujet de préoccupation dans les scénarios réels. Dans une implémentation d'arbre de recherche binaire, il est important de déterminer s'il faut utiliser un prédécesseur ordonné ou un successeur ordonné pour maintenir l'arbre correctement équilibré (souvent appelé arbre de recherche binaire auto-équilibré).
Le code source complet de cette implémentation d'arbre de recherche binaire peut être trouvé dans mon GitHub. Pour une implémentation alternative, vous pouvez également consulter le fork GitHub de Isaac Schlueter.
Cet article est reproduit à partir de : https://segmentfault.com/a/1190000020044659
Adresse originale en anglais : https://humanwhocodes.com/blog/2009/06/ 09/ Computer-science-in-Javascript-binary-search-tree-part-1/
Auteur : Nicholas C. Zakas
Tutoriel recommandé : "Vidéo JavaScript Tutoriel》
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!