Comment calculer π en utilisant la formule en python

Python utilise des formules pour calculer π : importez d'abord le module mathématique et le module temporel ; puis calculez Pi avec quelques décimales, le code est [print('n{:=^70}'.format( ' Le calcul démarre'))]; Enfin, le calcul est terminé, le code est [print('n{:=^70}']).

[Recommandations d'apprentissage associées :Tutoriel Python]

Comment calculer π à l'aide d'une formule en python :

1. 🎜>

Introduction à π

Pi est représenté par la lettre grecque π (prononcée pài). C'est une constante (approximativement égale à 3,141592654) et représente le rapport entre la circonférence et le diamètre de. un cercle. C'est un nombre décimal infini et non répétitif. Dans la vie quotidienne, 3,14 est généralement utilisé pour représenter pi pour le calcul approximatif. (John Wallis) a publié une monographie mathématique dans laquelle il a dérivé une formule et a découvert que pi est égal à. produit de fractions infinies. En 2015, des scientifiques de l’Université de Rochester ont découvert la même formule pour pi dans le calcul de la mécanique quantique du niveau d’énergie des atomes d’hydrogène. Le 14 mars 2019, Google a annoncé que pi avait désormais atteint 31 400 milliards. décimales. >

Ici, j'utilise une formule que je considère comme « bonne » à résoudre. C'est bien car les résultats du calcul sont relativement précis, mais le processus de calcul prend. longtemps. Apprenons ensemble ~~

• 2. Calcul approximatif de π

• 1. Formule de calcul.

　2. Explication de la méthode

Les numérateurs à droite des équations utilisées sont tous 1, et le dénominateur est un séquence croissante. À partir du premier terme, le signe du terme impair est positif, le signe du terme pair est négatif Plus le dénominateur du côté droit de l'équation est grand et petit, plus la valeur calculée de pi est précise ; en d'autres termes, plus il y a de termes sur le côté droit de l'équation, plus la valeur calculée est précise >

3 Implémentation du code (python)

 1 from math import fabs           #导入数学模块
 2 from time import perf_counter   #导入时间模块
 3 
 4 def Bar(i):         #动态文本条
 5     N = pow(10,level)
 6     a = int((i/N)*50)
 7     b = 50 - a
 8     Y , N = '*' * a , '.' * b
 9     print("\r计算中：{:3.0f}% [{}->{}] {:.2f}s"
10           .format(2*a,Y,N,perf_counter()),end='')
11     
12 level = eval(input('计算Pi精确到小数点后几位数：'))
13 print('\n{:=^70}'.format('计算开始'))
14 a,b,pi,tmp = 1,1,0,1
15 i = 0
16 '''
17 a 分子  |  b 分母  |  pi 圆周率
18 tmp 存储a/b的值    |  i  执行进度
19 '''
20 perf_counter()      #开始计时
21 while (fabs(tmp) >= pow(10,-level)): #计算Pi
22     pi += tmp
23     b += 2
24     a = -a
25     tmp = a/b
26     i += 2
27     Bar(i)          #调用函数，实时显示计算进度
28 
29 print('\n{:=^70}'.format('计算完成'))
30 print('\nPi的计算值为：{}'.format(round(pi*4,level))) #输出计算结果

<.>

4. Exemple d'image

Comme on peut le voir sur les trois images ci-dessus, il ne faut que 14,07 secondes pour être précis à 4 décimales, et il faut 124,61 secondes pour être précis à 6 décimales, et il faut 850/8 % = 10625 secondes pour être précis à 8 décimales, ce qui représente environ 177 minutes, soit 2,95 heures. Cette méthode est bonne, mais son calcul prend encore beaucoup de temps.

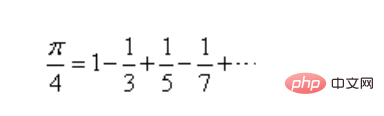
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!