Comment trouver une intégrale indéfinie dans Matlab
Comment trouver des intégrales indéfinies dans matlab : définissez d'abord les variables et fonctions indépendantes et visualisez l'image de la fonction puis calculez l'intégrale indéfinie de [y=x^2], utilisez la commande [int(y) ,x)] c'est-à-dire Can.

Méthode Matlab pour trouver des intégrales indéfinies :
1 Vous devez utiliser int(y,x[,range]) pour calculer des intégrales définies. et intégrales indéfinies cette fonction. Prenons maintenant y=x^2 comme exemple pour illustrer comment l'utiliser. Définissez d’abord les variables indépendantes et la fonction et affichez l’image de la fonction comme suit.
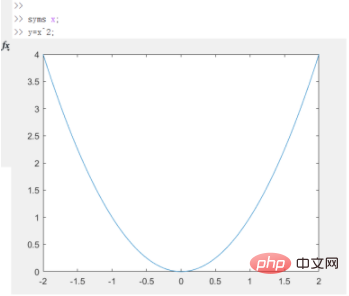
2. Pour calculer l'intégrale indéfinie de y=x^2, utilisez la commande int(y,x). Le résultat de l'intégrale est f=x^3/3, et l'image correspondante est la suivante.
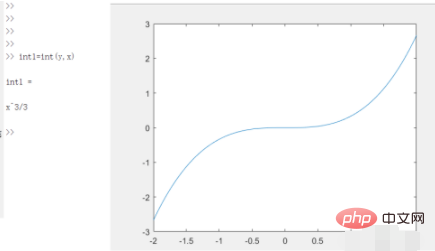
3. Si vous souhaitez calculer l'intégrale définie, vous devez ajouter les limites supérieure et inférieure de l'intégrale. Par exemple, voici l'intégrale définie de y=x^2 sur [-1,1] : int(y,x,-1,1)

4. Ensuite, donnons quelques exemples plus compliqués y=x^2*ln(1+x). Son image est la suivante :
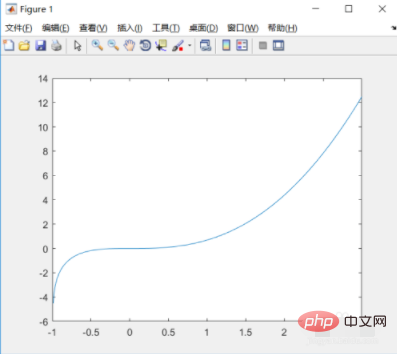
5. Utilisez la représentation symbolique pour obtenir son expression intégrale comme suit :
Si vous utilisez la méthode intégrale ordinaire par parties, vous avez besoin Il faut deux intégrales consécutives par parties pour éliminer l'exposant de puissance.

6. L'image de l'intégrale indéfinie obtenue ci-dessus et l'intégrale définie de la fonction originale sur [0,2] sont les suivantes
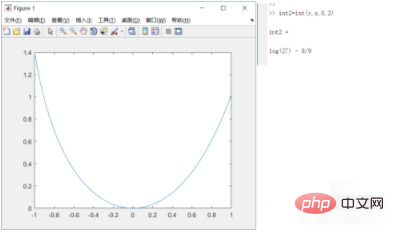
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Quelles sont les opérations Java fournies avec Matlab ?
May 03, 2023 pm 04:07 PM
Quelles sont les opérations Java fournies avec Matlab ?
May 03, 2023 pm 04:07 PM
1. Obtenez la position plein écran de la souris. Le coin supérieur gauche de l'écran est l'origine des coordonnées. Pour obtenir la position de la souris et la couleur des pixels de la souris, il est recommandé de l'utiliser en conjonction avec une boucle while ou une minuterie. fonction : importjava.awt.MouseInfo;mousepoint=MouseInfo.getPointerInfo().getLocation();mousepoint =[mousepoint.x,mousepoint.y]2 Obtenir le contenu actuel du presse-papiers importjava.awt.Toolkitimportjava.awt.datatransfer.DataFlavorclip=
 La différence entre Scilab et Matlab
Dec 11, 2023 am 11:13 AM
La différence entre Scilab et Matlab
Dec 11, 2023 am 11:13 AM
La différence entre scilab et matlab : 1. Symboles d'annotation ; 2. Représentation des variables prédéfinies ; 3. Utilisation des opérateurs ; 4. Définition et appel des matrices ; 6. Types de données ; ; 8. Interface graphique ; 9. Support communautaire et écosystème ; 10. Compatibilité multiplateforme ; Introduction détaillée : 1. Symboles de commentaires. Dans Scilab, les commentaires sont guidés par "//", tandis que dans Matlab, les commentaires sont guidés par "%" 2. Représentation des variables prédéfinies dans Scilab, etc.
 Comment utiliser fprintf dans matlab
Sep 28, 2023 pm 04:28 PM
Comment utiliser fprintf dans matlab
Sep 28, 2023 pm 04:28 PM
fprintf est une fonction de MATLAB utilisée pour formater la sortie. La syntaxe de base de fprintf est "fprintf(fileID, format, A)", où fileID est un identifiant utilisé pour spécifier le fichier à écrire. Si vous souhaitez écrire des données dans la fenêtre de commande, vous pouvez utiliser 1 comme fileID La valeur. of format est une chaîne utilisée pour spécifier le format de sortie, et A est les données à sortir.
 Comment modifier les coordonnées dans matlab
Dec 15, 2023 am 10:40 AM
Comment modifier les coordonnées dans matlab
Dec 15, 2023 am 10:40 AM
Dans MATLAB, vous pouvez utiliser la fonction "set" pour modifier les propriétés des axes d'un graphique. Introduction détaillée : 1. Modifiez la plage de l'axe des coordonnées : set(gca, 'XLim', [0 10], 'YLim', [0 10]) 2. Modifiez l'étiquette de l'axe des coordonnées : set(gca, 'XLabel', 'Mon axe X', 'YLabel', 'Mon axe Y'); 3. Modifier l'échelle de l'axe des coordonnées, etc.
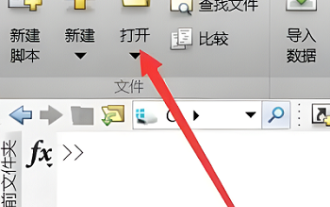 Comment exécuter m-file dans matlab - Tutoriel sur l'exécution de m-file dans matlab
Mar 04, 2024 pm 02:13 PM
Comment exécuter m-file dans matlab - Tutoriel sur l'exécution de m-file dans matlab
Mar 04, 2024 pm 02:13 PM
Savez-vous comment exécuter des fichiers m dans matlab ? Ci-dessous, l'éditeur vous proposera un tutoriel sur la façon d'exécuter des fichiers m dans matlab. J'espère que cela vous sera utile. Apprenons avec l'éditeur ! logiciel et sélectionnez le coin supérieur gauche "Ouvrir", comme indiqué dans l'image ci-dessous. 2. Sélectionnez ensuite le fichier m à exécuter et ouvrez-le, comme indiqué dans la figure ci-dessous. 3. Appuyez sur F5 dans la fenêtre pour exécuter le programme, comme indiqué dans la figure ci-dessous. 4. Nous pouvons afficher les résultats en cours d'exécution dans la fenêtre de ligne de commande et dans l'espace de travail, comme le montre la figure ci-dessous. 5. Vous pouvez également exécuter le fichier en cliquant directement sur « Exécuter », comme le montre la figure ci-dessous. 6. Enfin, vous pouvez afficher les résultats d'exécution du fichier m dans la fenêtre de ligne de commande et l'espace de travail, comme indiqué dans la figure ci-dessous. Ce qui précède est la méthode matlab que l'éditeur vous a présentée
 Comment arrêter d'exécuter des commandes dans Matlab
Jan 14, 2021 am 11:46 AM
Comment arrêter d'exécuter des commandes dans Matlab
Jan 14, 2021 am 11:46 AM
Comment arrêter l'exécution des commandes dans Matlab : 1. Sélectionnez un programme et cliquez sur l'icône d'exécution ; 2. Cliquez sur l'icône de pause ci-dessus pour arrêter temporairement l'exécution du programme. 3. Cliquez pour quitter le débogage pour forcer l'arrêt du programme occupé.
 Comment convertiriez-vous le code MATLAB en code Python ?
Aug 19, 2023 pm 10:53 PM
Comment convertiriez-vous le code MATLAB en code Python ?
Aug 19, 2023 pm 10:53 PM
MATLAB est un langage de programmation populaire largement utilisé dans les domaines de l'ingénierie et des sciences, mais Python devient rapidement le langage de choix pour de nombreux programmeurs en raison de sa flexibilité et de son adaptabilité. Si vous souhaitez convertir du code MATLAB en code Python, cela peut sembler très difficile au début. Cependant, avec les connaissances et la bonne approche, vous pouvez rendre le processus beaucoup plus facile. Voici quelques étapes pour vous aider à convertir du code MATLAB en Python : Étape 1 : Familiarisez-vous avec la syntaxe Python Python et MATLAB ont une syntaxe unique, vous devez donc vous familiariser avec la syntaxe Python avant de commencer à convertir votre code. Passez du temps à comprendre les bases de la syntaxe Python, y compris les variables et les types de données.
 Comment utiliser la fonction GridData de Matlab
Dec 15, 2023 am 10:11 AM
Comment utiliser la fonction GridData de Matlab
Dec 15, 2023 am 10:11 AM
La fonction griddata est utilisée pour interpoler la valeur Z correspondante à une coordonnée donnée (X, Y), quadrillant ainsi un ensemble de données tridimensionnelles (x, y, z). Son utilisation est "griddata(x, y, z, xi, yi, method)".





