Le parcours en largeur d'un graphe est un parcours horizontal en premier, similaire au parcours couche par couche d'un arbre binaire. Le parcours en largeur recherche et parcourt le long de la largeur de l'arborescence à partir du nœud racine, c'est-à-dire en parcourant de manière hiérarchique chaque couche est visitée séquentiellement de haut en bas, et dans chaque couche, de gauche à droite (ou de droite). à gauche) Pour accéder aux nœuds, après avoir accédé à un niveau, entrez dans le niveau suivant jusqu'à ce qu'aucun nœud ne soit accessible.
Semblable au parcours d'arbre, le parcours de graphe commence également à partir d'un certain point du graphique, puis le parcourt en fonction de une certaine méthode. Tous les sommets du graphique ne sont visités qu’une seule fois.
Mais le parcours de graphes est plus compliqué que celui des arbres. Étant donné que n'importe quel sommet du graphique peut être adjacent à d'autres sommets, les sommets visités doivent être enregistrés pendant le parcours du graphique pour éviter des visites répétées.
Selon les différents chemins de recherche, nous pouvons diviser les méthodes de parcours graphique en deux types : la recherche en largeur d'abord et la recherche en profondeur d'abord.
La paire de sommets (u, v) est non ordonnée, c'est-à-dire (u, v ) et (v, u) sont du même côté. Généralement exprimé par une paire de parenthèses.
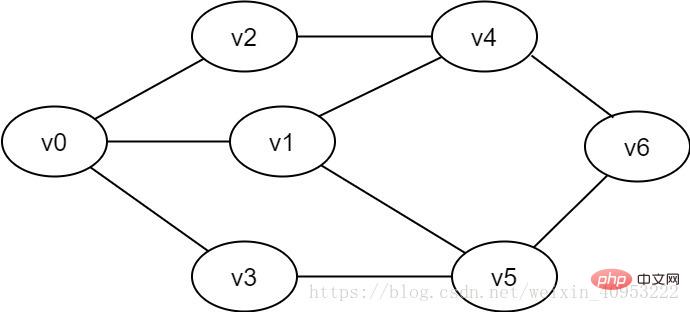
Figure 2-1-1 Exemple de graphe non orienté
La paire de sommets
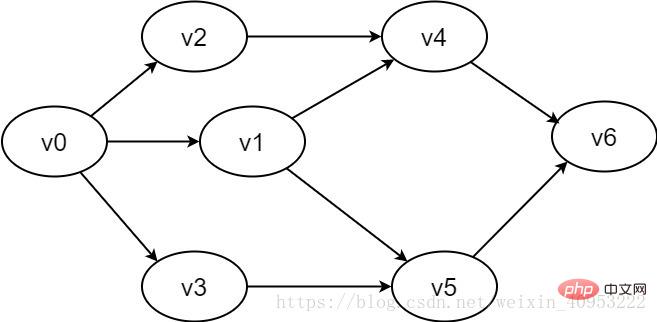
Figure 2-1-2 Exemple de graphe orienté
Chaque arête du graphique peut avoir une valeur avec une certaine signification, appelée le poids de l'arête. Ce type de graphe pondéré s’appelle un réseau.
Graphe connecté : Dans un graphe non orienté G, s'il existe un chemin du sommet v au sommet v', alors v et v' sont dits être connecté. Si deux sommets v, v'∈V dans le graphe, et v et v' sont connectés, alors G est dit être un graphe connecté. Les deux graphiques ci-dessus sont tous deux des graphiques connectés.
Graphe déconnecté : S'il y a une déconnexion entre v et v' dans le graphe non orienté G, alors G est dit être un graphe déconnecté.
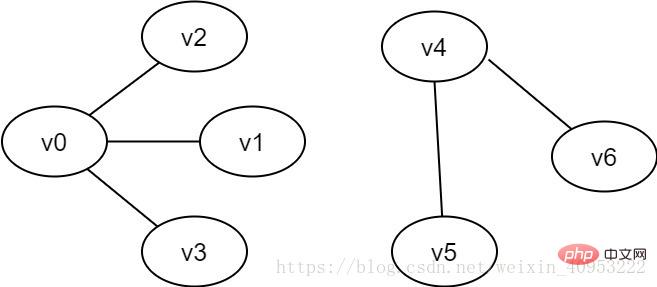
Figure 2-3 Exemple de graphique non connecté
La recherche en largeur d'abord est similaire au processus de parcours hiérarchique d'un arbre. Il doit être mis en œuvre à l'aide d'une file d'attente. Comme le montre la figure 2-1-1, si nous voulons parcourir chaque sommet de v0 à v6, nous pouvons définir v0 comme première couche, v1, v2 et v3 comme deuxième couche, v4 et v5 comme troisième couche, et v6 Pour la quatrième couche, chaque sommet de chaque couche est parcouru un par un.
Le processus spécifique est le suivant :
1. Préparation : Créer un tableau visité pour enregistrer les sommets visités ; créer une file d'attente pour stocker les sommets de chaque couche d'initialisation ;
2. Commencez la visite à partir de v0 dans l'image, définissez la valeur du tableau visité[v0] sur true et ajoutez v0 à la file d'attente.
3. Tant que la file d'attente n'est pas vide, répétez les opérations suivantes :
(1) Pointez-vous en haut de l'équipe pour sortir de la file d'attente.
(2) Vérifiez tour à tour tous les sommets adjacents w de u Si la valeur de visité[w] est fausse, visitez w, définissez visité[w] sur vrai et ajoutez w à la file d'attente.
Le blanc signifie qu'il n'a pas été visité, le gris signifie qu'il est sur le point d'être visité et le noir signifie qu'il a été visité.
tableau visité : 0 signifie non visité, 1 signifie visité.
File d'attente : les éléments sortent de la tête de la file d'attente et les éléments entrent par la queue.
1. Initialement, tous les sommets n'ont pas été visités, le tableau visité est initialisé à 0 et il n'y a aucun élément dans la file d'attente.
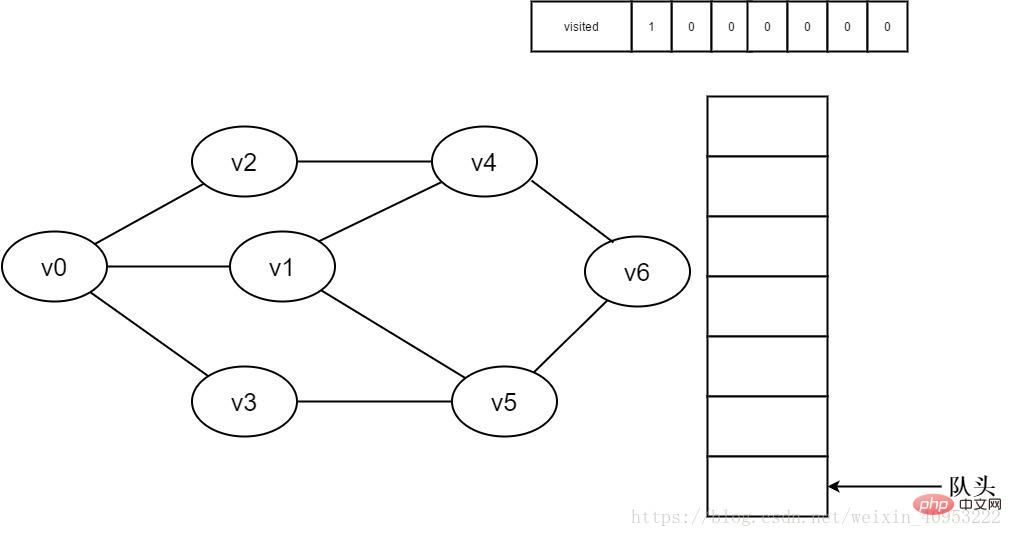
Figure 3-2-1
2. Vertex v0 est sur le point d'être. visité.
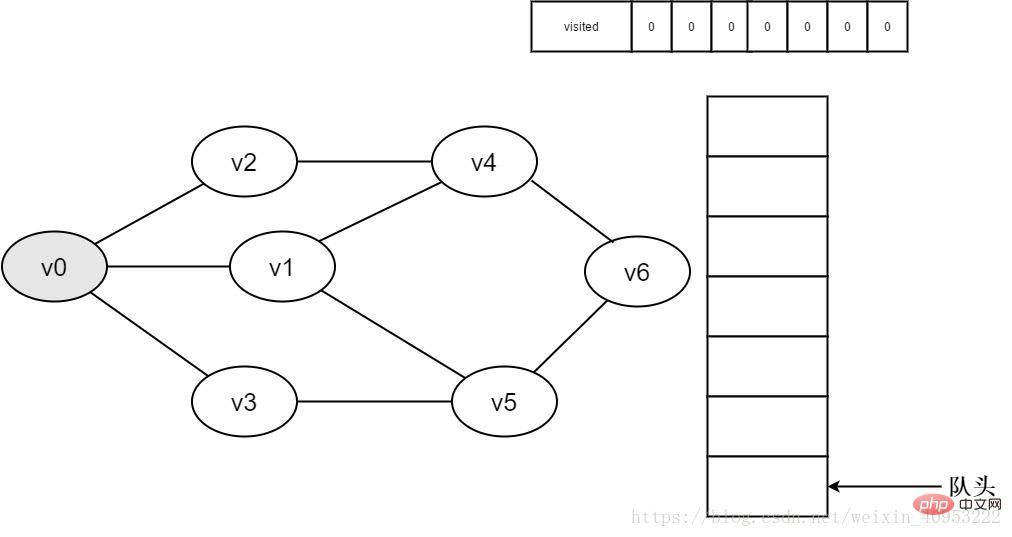
Figure 3-2-2
3. Visiter le sommet v0 et le lieu visité[0 Le la valeur de ] est 1 et v0 est ajouté à la file d'attente en même temps.
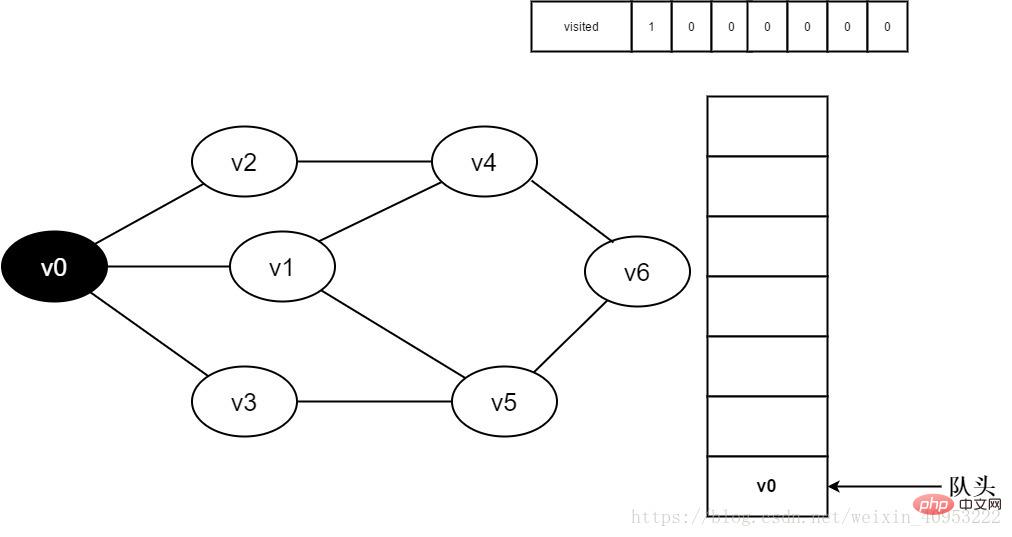
Figure 3-2-3
4. Retirez v0 de la file d’attente et visitez le point adjacent v2. Déterminez visité[2], car la valeur de visité[2] est 0, visitez v2.
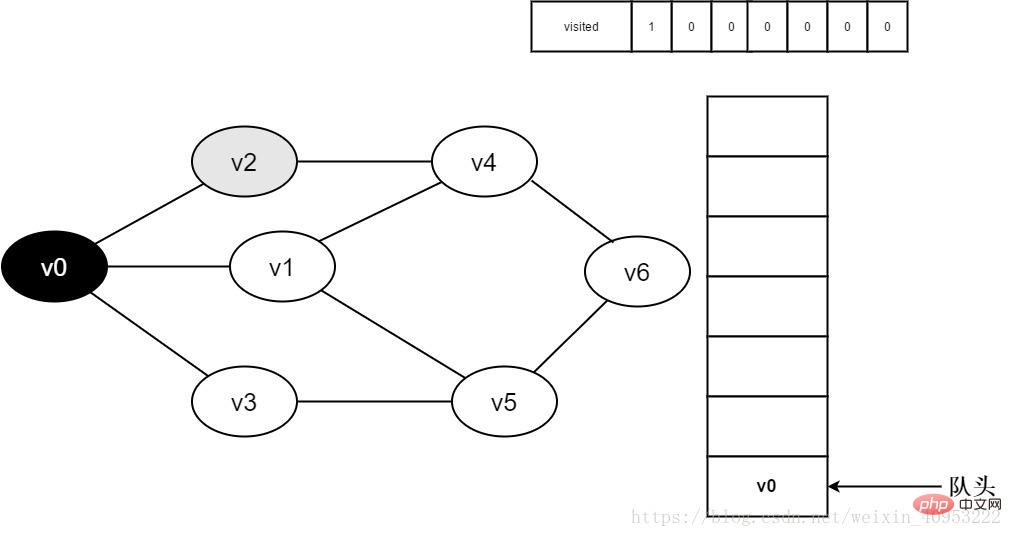
Figure 3-2-4
5. Ensemble visité[2] à 1 et v2 Rejoindre l'équipe .
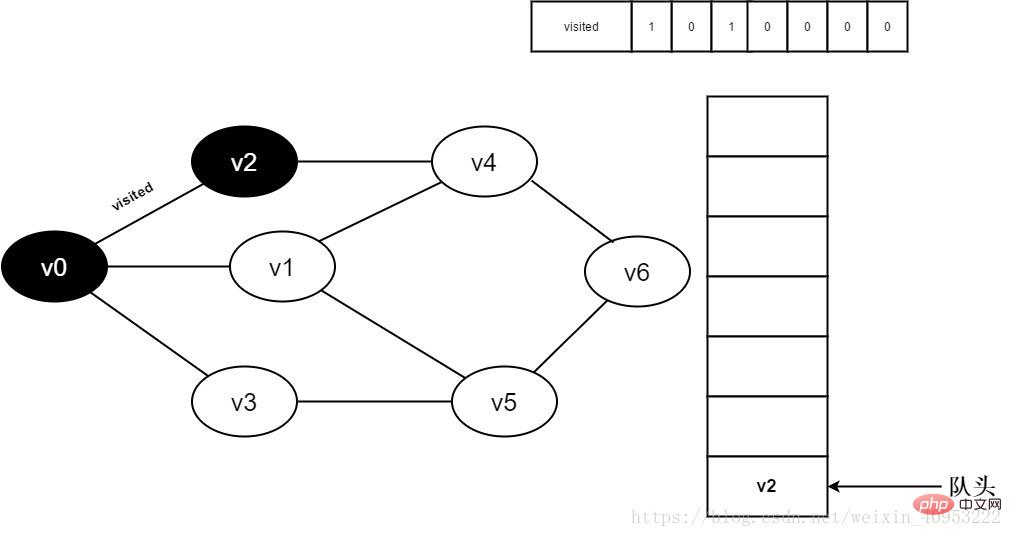
Figure 3-2-5
6. Visitez le point v0 adjacent v1. Déterminez visité[1], car la valeur de visité[1] est 0, visitez v1.
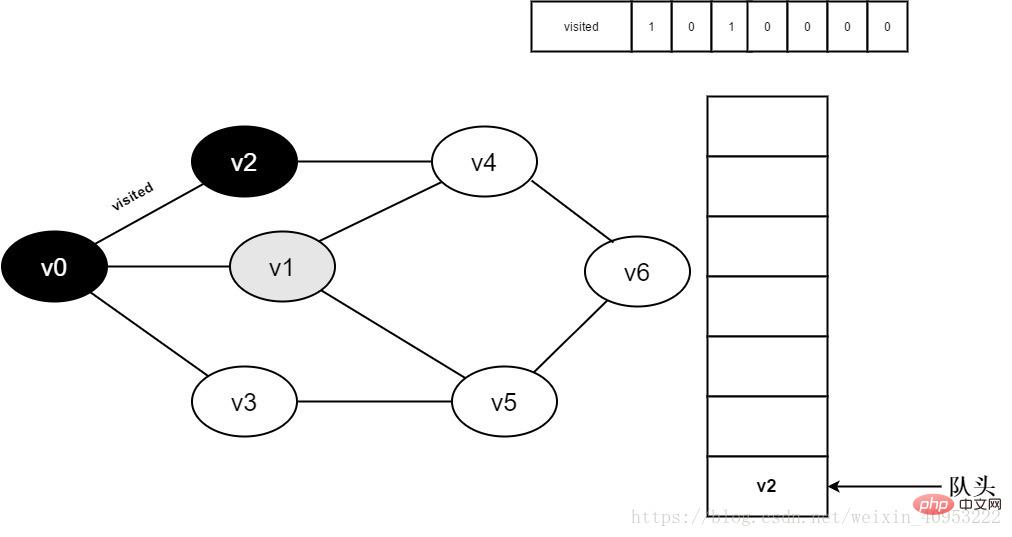
Figure 3-2-6
7. Ensemble visité[1] à 0 et v1 Rejoindre l'équipe .
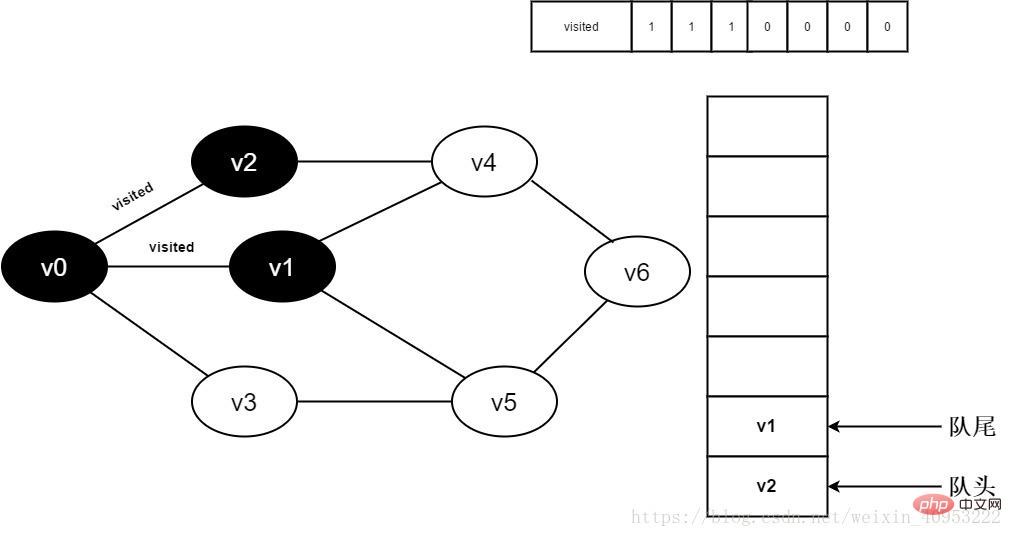
Figure 3-2-7
8. Juge visité[3] car sa valeur est 0 , accès v3. Définissez visité[3] sur 0 et mettez la v3 en file d'attente.
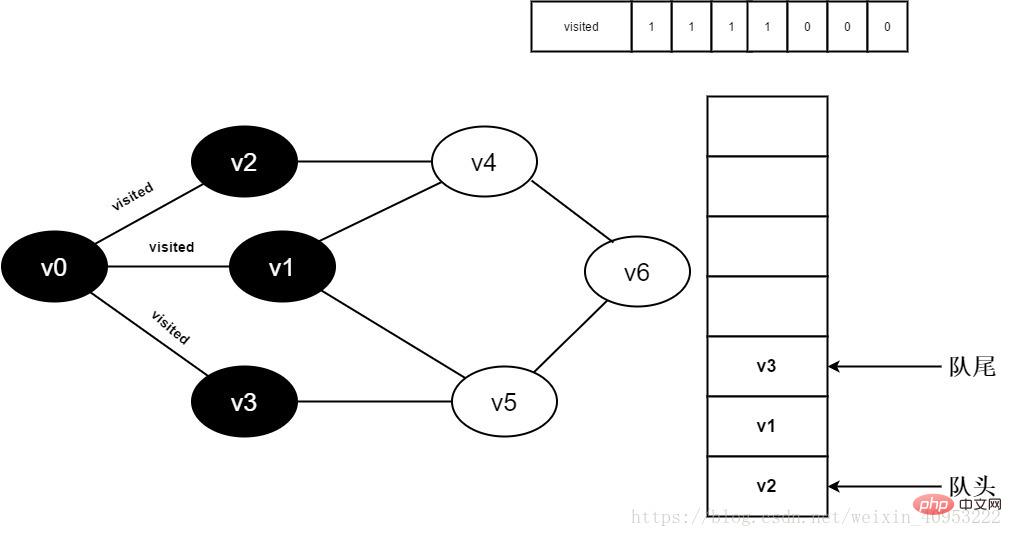
Figure 3-2-8
Tous les points adjacents de 9.v0 ont été visités. Retirez l'élément principal v2 de la file d'attente et commencez à visiter tous les points adjacents de v2.
Commencez à visiter v2 au point adjacent v0, et jugez visité[0], car sa valeur est 1, aucune visite n'est effectuée.
Continuez à visiter v2 le point adjacent v4, jugez visité[4], car sa valeur est 0, visitez v4, comme indiqué ci-dessous :
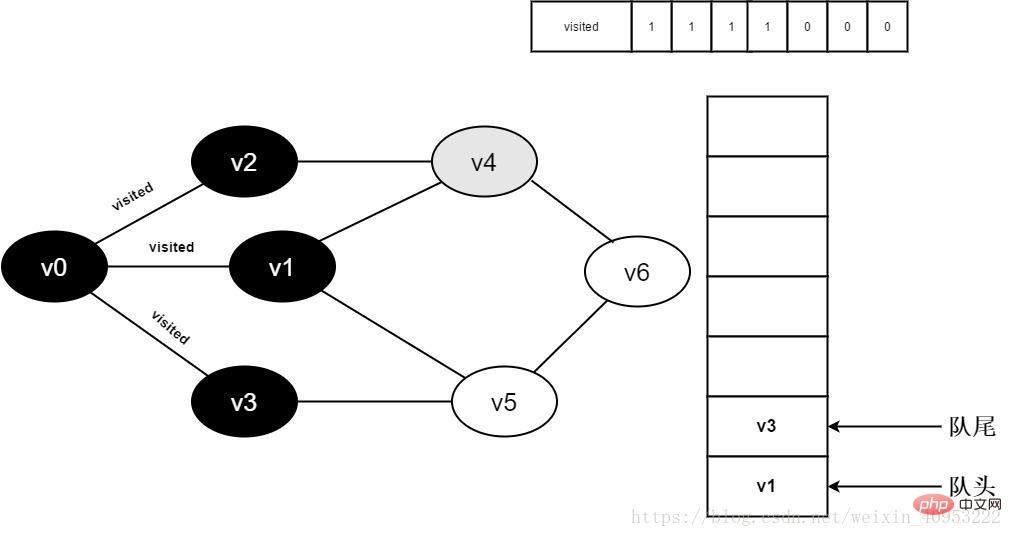
Figure 3-2-9
10. Définissez visité[4] sur 1 et ajoutez la v4 à la file d'attente.
Figure 3-2-10
Tous les points adjacents de 11.v2 ont été visités. Retirez l'élément principal v1 de la file d'attente et commencez à visiter tous les points adjacents de v1.
Commencez à visiter v1 au point adjacent v0, car la valeur visitée[0] est 1, aucune visite n'est effectuée.
Continuez à visiter v1 le point adjacent v4, car la valeur de visité[4] est 1, aucune visite n'est effectuée.
Continuez à visiter v1 le point adjacent v5, car la valeur visitée[5] est 0, visitez v5, comme indiqué ci-dessous :
Fig. 3-2-11
12. Réglez visité[5] sur 1 et ajoutez la v5 à la file d'attente.
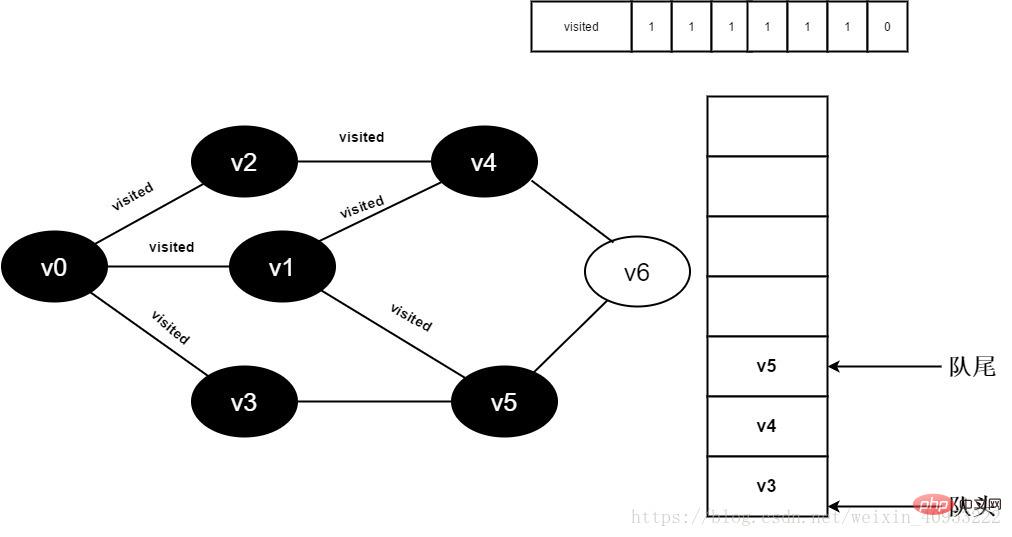
Figure 3-2-12
Tous les points adjacents de 13.v1 ont été visités, et l'élément de tête v3 est retiré de la file d'attente et commence à accéder à tous les points adjacents de la v3.
Commencez à visiter v3 au point adjacent v0, car la valeur visitée[0] est 1, aucune visite n'est effectuée.
Continuez à visiter v3 le point adjacent v5, car la valeur visitée[5] est 1, aucune visite n'est effectuée.
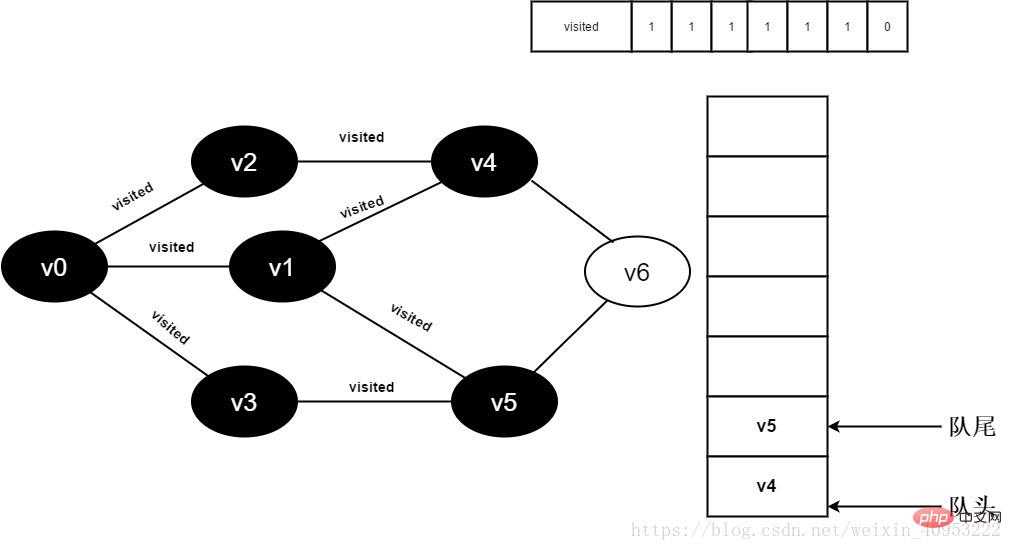
Figure 3-2-13
Tous les points adjacents de 14.v3 ont été visités, et La tête l'élément v4 est retiré de la file d'attente et commence à visiter tous les points adjacents de v4.
Commencez à visiter le point adjacent v2 de v4 Comme la valeur de visité[2] est 1, aucune visite n'est effectuée.
Continuez à visiter le point adjacent v6 de v4, car la valeur de visité[6] est 0, visitez v6, comme indiqué ci-dessous :
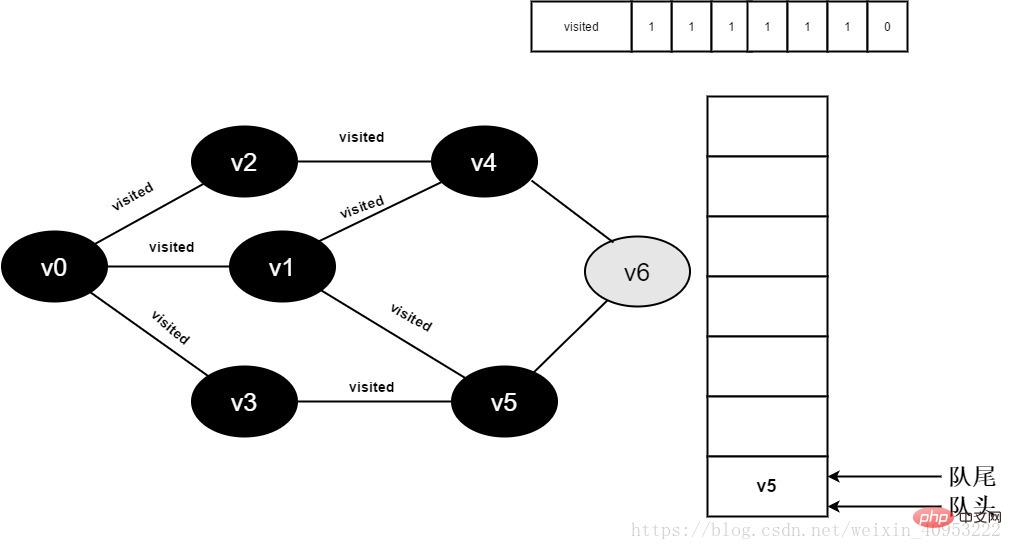
Figure 3-2-14
15. Définissez la valeur de visité[6] sur 1 et ajoutez v6 à la file d'attente.
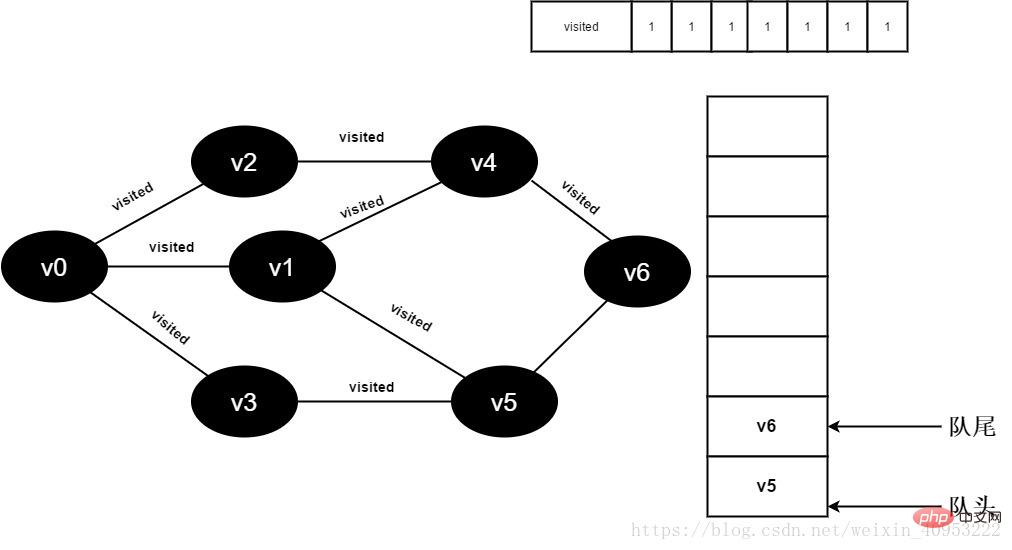
Figure 3-2-15
Tous les points adjacents de 16.v4 ont été visités, et La tête l'élément v5 est retiré de la file d'attente et commence à visiter tous les points adjacents de v5.
Commencer à visiter le point voisin v5 v3 Comme la valeur de visité[3] est 1, aucune visite ne sera effectuée.
Continuez à visiter le point voisin v5 v6, car la valeur de visité[6] est 1, aucune visite n'est effectuée.
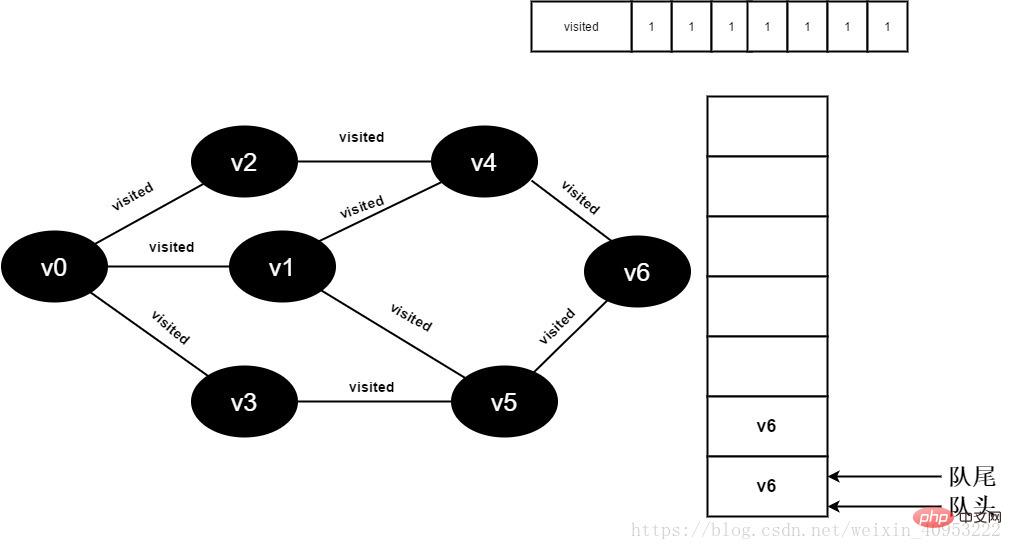
Figure 3-2-16
Tous les points adjacents de 17.v5 ont été visités, et La tête l'élément v6 est retiré de la file d'attente et commence à visiter tous les points adjacents de v6.
Commencez à visiter le point voisin v6 v4, car la valeur de visité[4] est 1, aucune visite n'est effectuée.
Continuez à visiter le point voisin v6 v5, car la valeur de visité[5] est 1, donc aucune visite n'est effectuée.
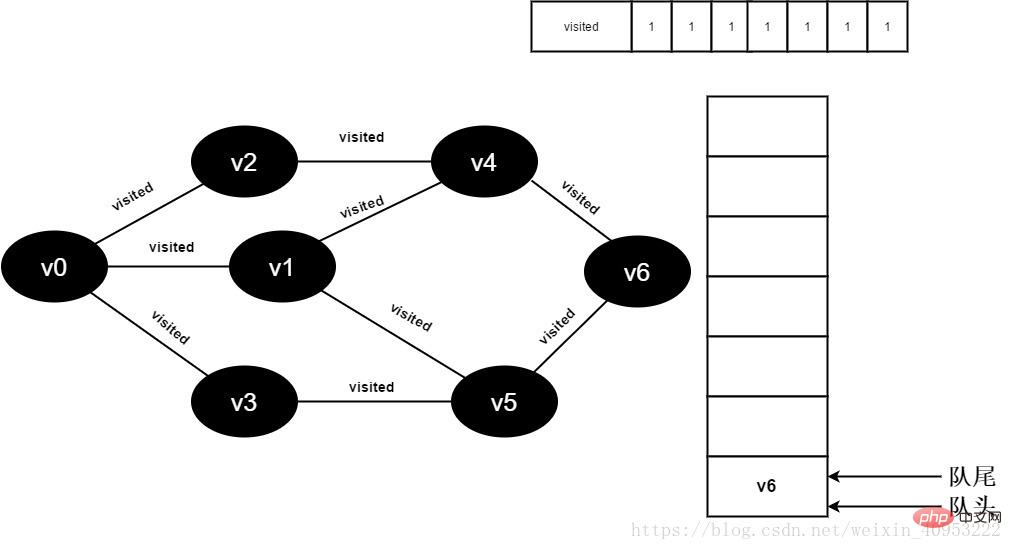
Figure 3-2-17
18 La file d'attente est vide, quittez la boucle et tous les sommets ont été visités. .
Figure 3-2-18
/*一些量的定义*/ queue<char> q; //定义一个队列，使用库函数queue #define MVNum 100 //表示最大顶点个数 bool visited[MVNum]; //定义一个visited数组，记录已被访问的顶点
/*邻接矩阵存储表示*/
typedef struct AMGraph
{
char vexs[MVNum]; //顶点表
int arcs[MVNum][MVNum]; //邻接矩阵
int vexnum, arcnum; //当前的顶点数和边数
}
AMGraph;/*找到顶点v的对应下标*/
int LocateVex(AMGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.vexs[i] == v)
return i;
}/*采用邻接矩阵表示法，创建无向图G*/
int CreateUDG_1(AMGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数，总边数
getchar(); //获取'\n’，防止其对之后的字符输入造成影响
for (i = 0; i < G.vexnum; i++)
scanf("%c", &G.vexs[i]); //依次输入点的信息
for (i = 0; i < G.vexnum; i++)
for (j = 0; j < G.vexnum; j++)
G.arcs[i][j] = 0; //初始化邻接矩阵边，0表示顶点i和j之间无边
for (k = 0; k < G.arcnum; k++)
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
G.arcs[i][j] = G.arcs[j][i] = 1; //1表示顶点i和j之间有边，无向图不区分方向
}
return 1;
}/*采用邻接矩阵表示图的广度优先遍历*/
void BFS_AM(AMGraph &G,char v0)
{
/*从v0元素开始访问图*/
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队，开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边，且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}/*找到顶点对应的下标*/
int LocateVex(ALGraph &G, char v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (v == G.vertices[i].data)
return i;
}/*邻接表存储表示*/
typedef struct ArcNode //边结点
{
int adjvex; //该边所指向的顶点的位置
ArcNode *nextarc; //指向下一条边的指针
int info; //和边相关的信息，如权值
}ArcNode;
typedef struct VexNode //表头结点
{
char data;
ArcNode *firstarc; //指向第一条依附该顶点的边的指针
}VexNode,AdjList[MVNum]; //AbjList表示一个表头结点表
typedef struct ALGraph
{
AdjList vertices;
int vexnum, arcnum;
}ALGraph;/*采用邻接表表示法，创建无向图G*/
int CreateUDG_2(ALGraph &G)
{
int i, j, k;
char v1, v2;
scanf("%d%d", &G.vexnum, &G.arcnum); //输入总顶点数，总边数
getchar();
for (i = 0; i < G.vexnum; i++) //输入各顶点，构造表头结点表
{
scanf("%c", &G.vertices[i].data); //输入顶点值
G.vertices[i].firstarc = NULL; //初始化每个表头结点的指针域为NULL
}
for (k = 0; k < G.arcnum; k++) //输入各边，构造邻接表
{
getchar();
scanf("%c%c", &v1, &v2); //输入一条边依附的两个顶点
i = LocateVex(G, v1); //找到顶点i的下标
j = LocateVex(G, v2); //找到顶点j的下标
ArcNode *p1 = new ArcNode; //创建一个边结点*p1
p1->adjvex = j; //其邻接点域为j
p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; // 将新结点*p插入到顶点v1的边表头部
ArcNode *p2 = new ArcNode; //生成另一个对称的新的表结点*p2
p2->adjvex = i;
p2->nextarc = G.vertices[j].firstarc;
G.vertices[j].firstarc = p1;
}
return 1;
}/*采用邻接表表示图的广度优先遍历*/
void BFS_AL(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队，开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}/*广度优先搜索非连通图*/
void BFSTraverse(AMGraph G)
{
int v;
for (v = 0; v < G.vexnum; v++)
visited[v] = 0; //将visited数组初始化
for (v = 0; v < G.vexnum; v++)
if (!visited[v]) BFS_AM(G, G.vexs[v]); //对尚未访问的顶点调用BFS
}La recherche en profondeur d'abord est similaire à la traversée pré-commandée d'un arbre, en particulier. Le processus est le suivant :
Préparation : créez un tableau visité pour enregistrer tous les sommets visités.
1. À partir de la v0 sur l'image, visitez la v0.
2. Trouvez le premier point adjacent non visité de v0 et visitez le sommet. Utilisez ce sommet comme nouveau sommet et répétez cette étape jusqu'à ce que le sommet que vous venez de visiter n'ait plus de sommets adjacents non visités.
3. Revenez au sommet précédemment visité qui a encore des points adjacents non visités et continuez à visiter le prochain point directeur non visité du sommet.
4. Répétez les étapes 2 et 3 jusqu'à ce que tous les sommets soient visités et que la recherche se termine.
1 Initialement, tous les sommets n'ont pas été visités et le tableau visité est vide.
Figure 4-2-1
2. La v0 est sur le point d'être consultée.
Figure 4-2-2
3. Visitez la v0 et l'ensemble visité[0] Le la valeur est fixée à 1.
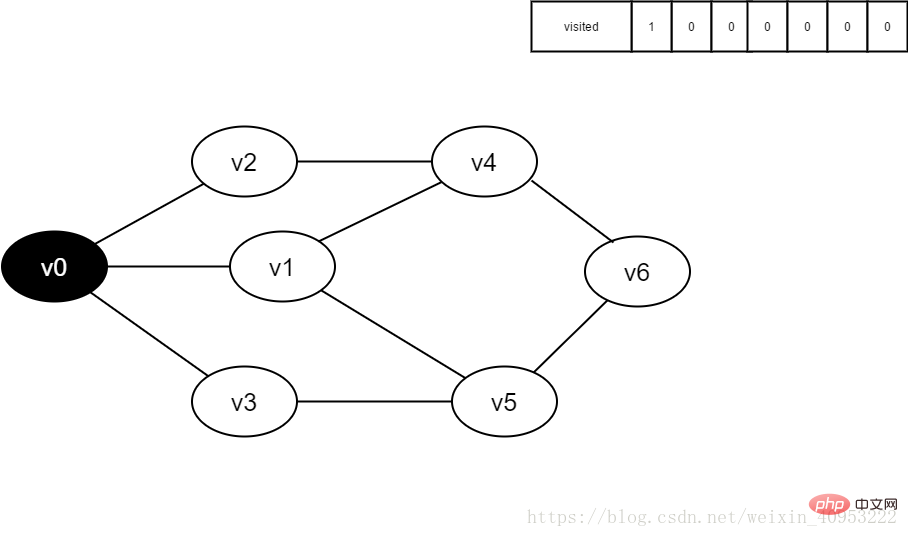
Figure 4-2-3
4 Visiter le point adjacent v2 de v0 et déterminer visité [2], puisque sa valeur est 0, on accède à v2.
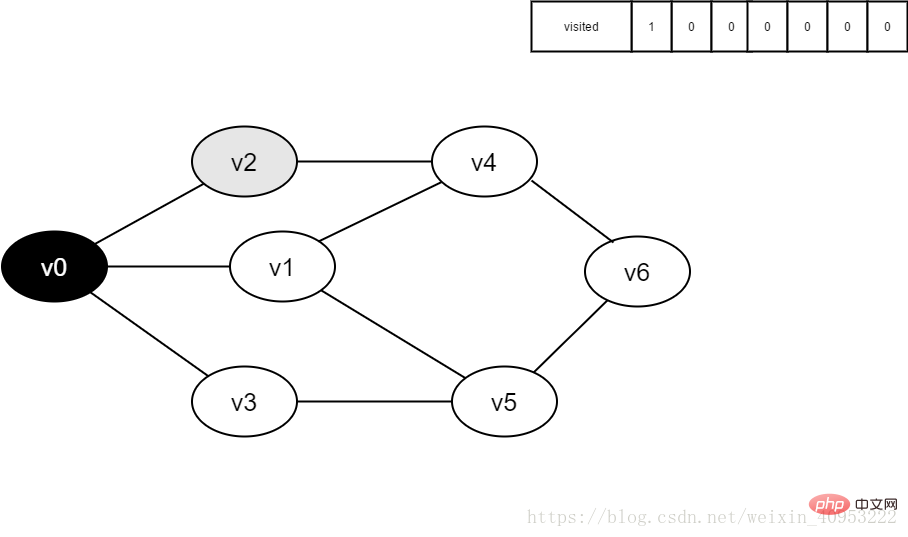
Figure 4-2-4
5. Définir visité[2] à 1.
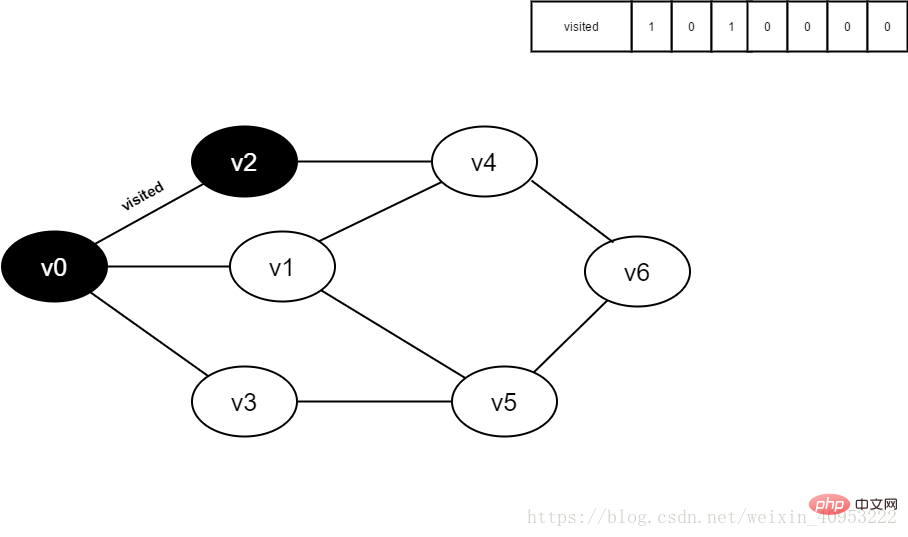
Figure 4-2-5
6. Visiter le point adjacent v0 de v2 et déterminer visité [0], dont la valeur est 1, n'est pas accessible.
Continuez à visiter le point adjacent v4 de v2, jugez visité[4], sa valeur est 0, et visitez v4.
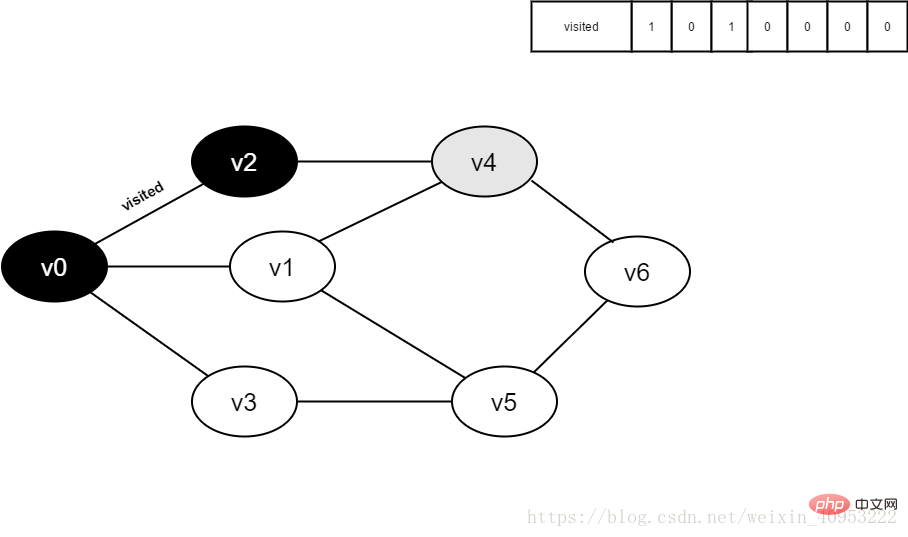
Figure 4-2-6
7. Définir visité[4] à 1.
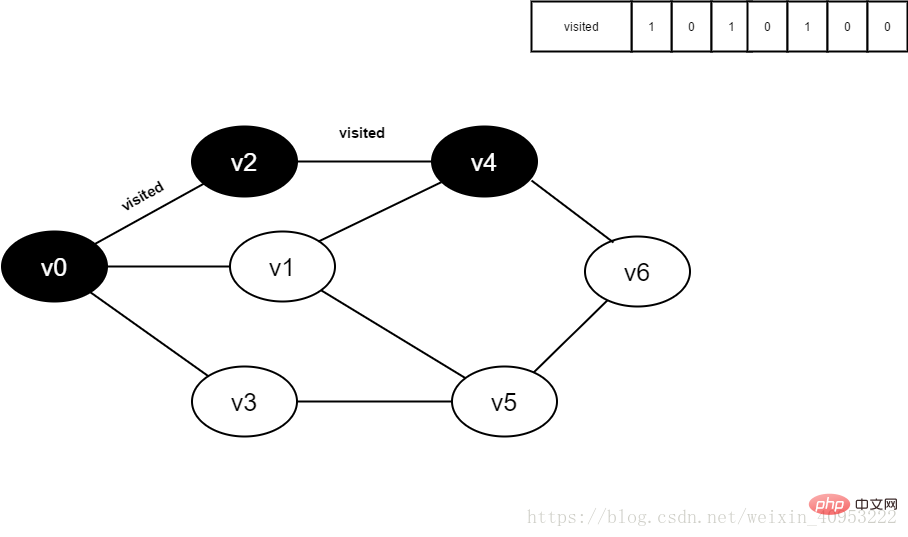
Figure 4-2-7
8 Visiter le point adjacent v1 de v4, déterminer visité[1], et sa valeur est 0, accédez à la v1.
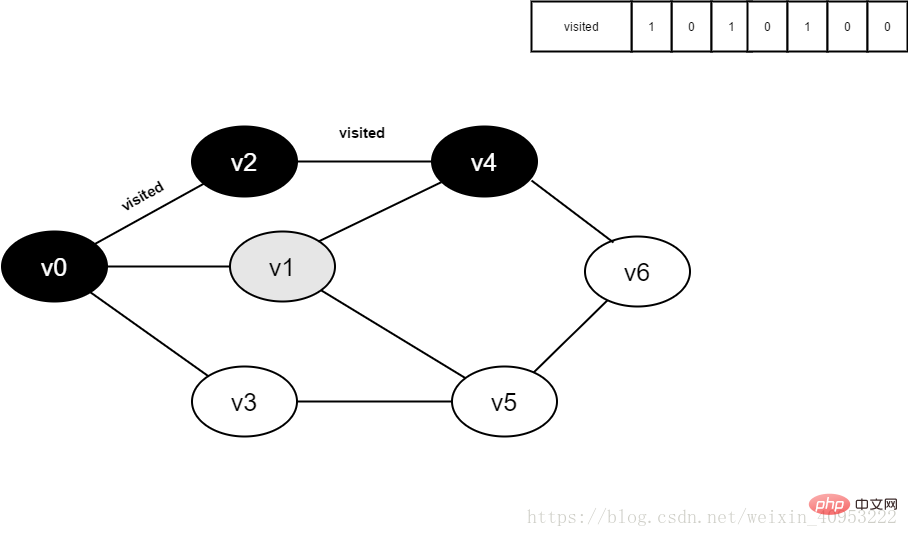
Figure 4-2-8
9. Ensemble visité[1] à 1.
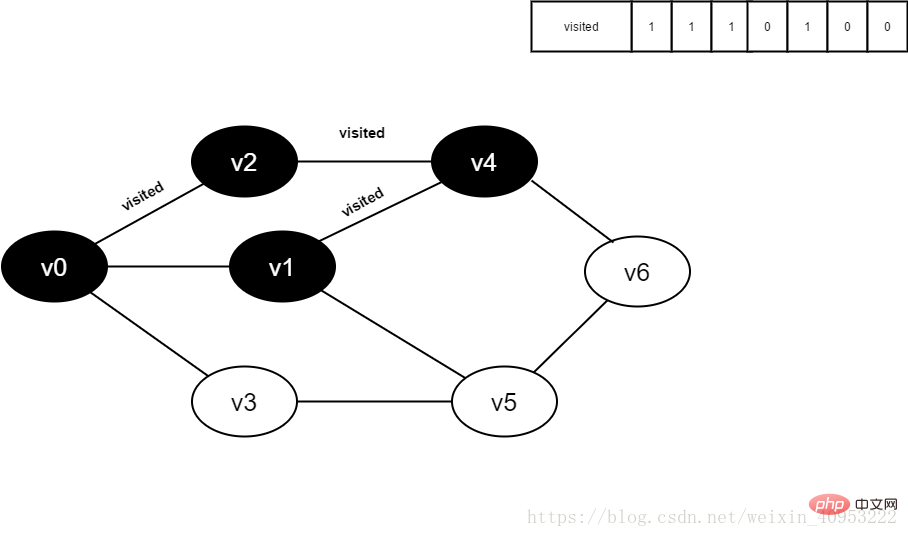
Figure 4-2-9
10 Visiter le point adjacent v0 de v1 et déterminer. visité [0], dont la valeur est 1, n'est pas accessible.
Continuez à visiter le point adjacent v4 de v1, jugez visité[4], sa valeur est 1, et ne visitez pas.
Continuez à visiter le point adjacent v5 de v1, interprétez visité[5], sa valeur est 0, visitez v5.
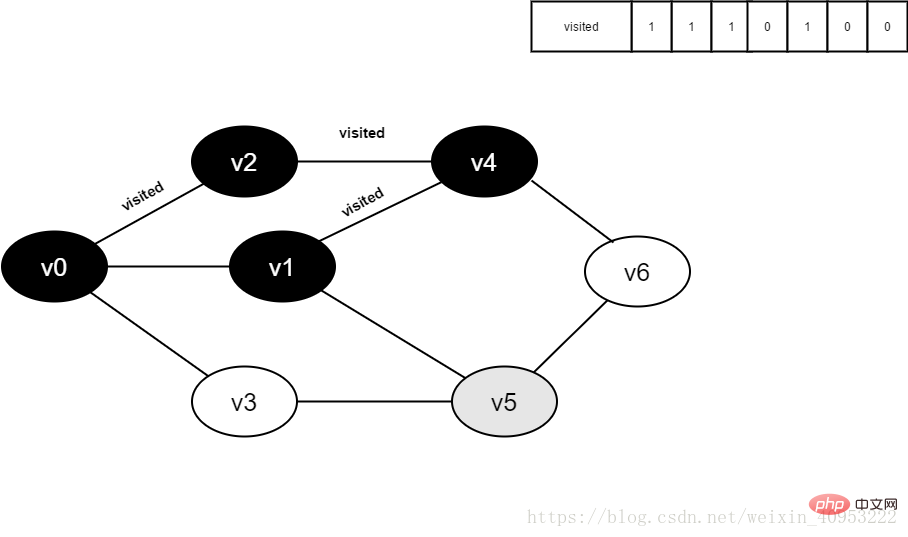
Figure 4-2-10
11. Ensemble visité[5] à 1.
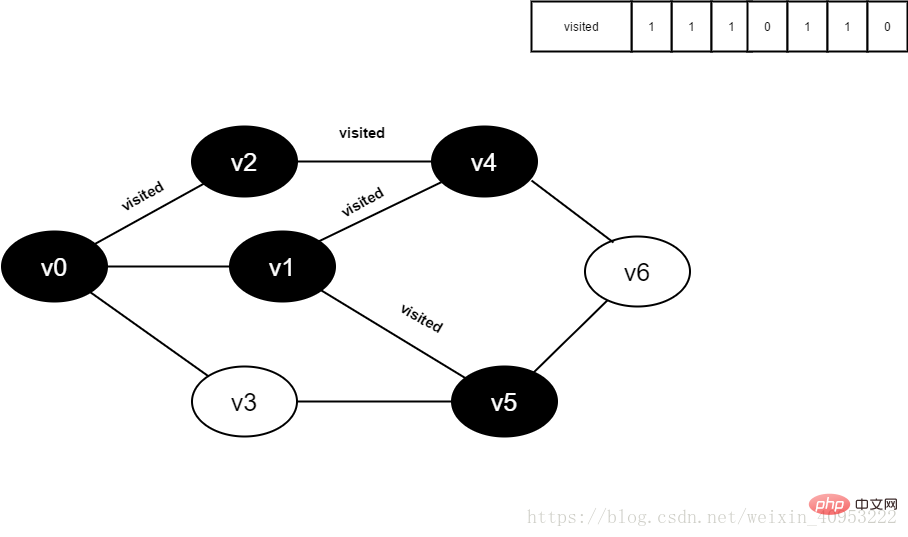
Figure 4-2-11
12 Visiter le point adjacent v1 de v5 et déterminer visité [1], dont la valeur est 1, n'est pas accessible.
Continuez à visiter le point adjacent v3 de v5, jugez visité[3], sa valeur est 0, visitez v3.
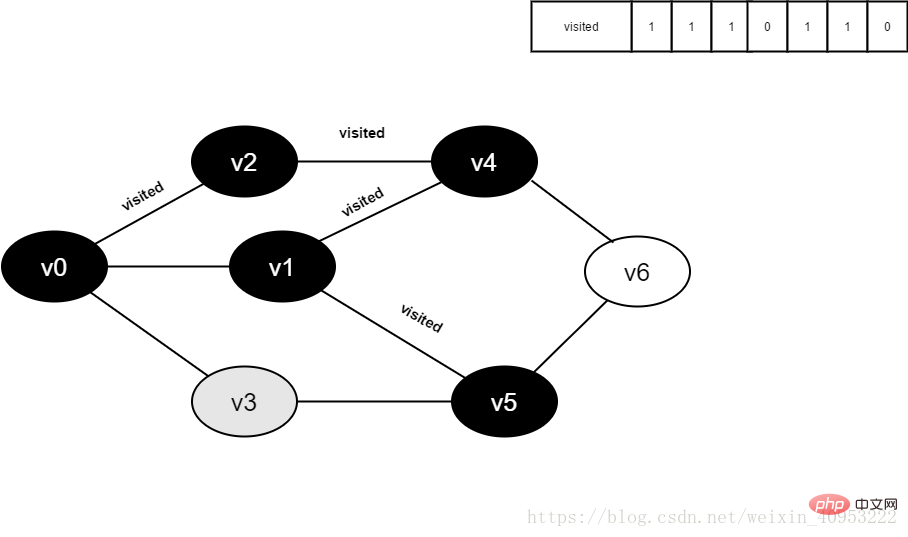
图4-2-12
13.将visited[1]置为1。
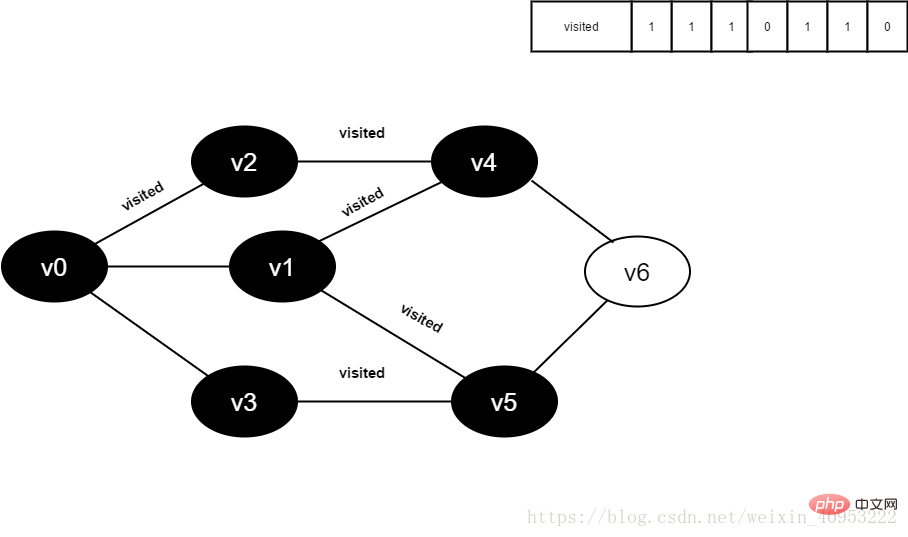
图4-2-13
14.访问v3的邻接点v0，判断visited[0]，其值为1，不访问。
继续访问v3的邻接点v5，判断visited[5]，其值为1，不访问。
v3所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5所有邻接点。
访问v5的邻接点v6，判断visited[6]，其值为0，访问v6。
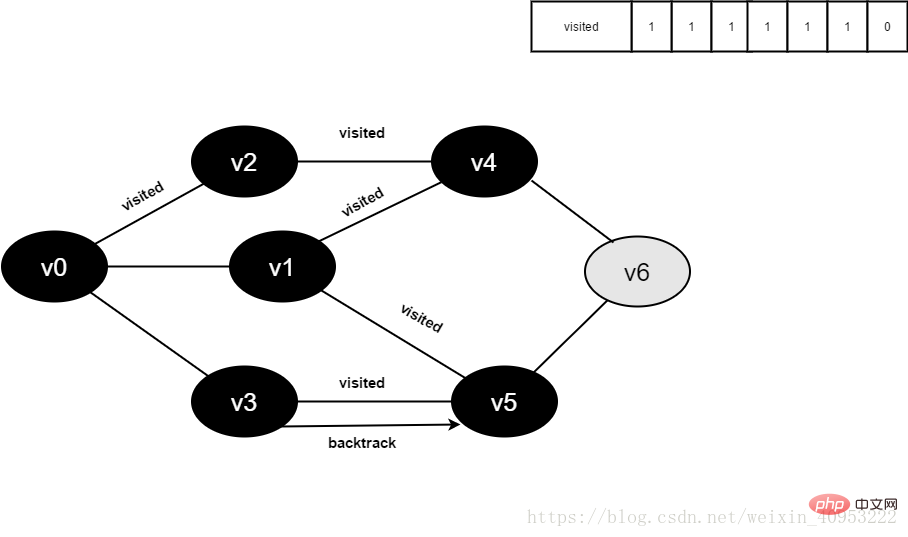
图4-2-14
15.将visited[6]置为1。
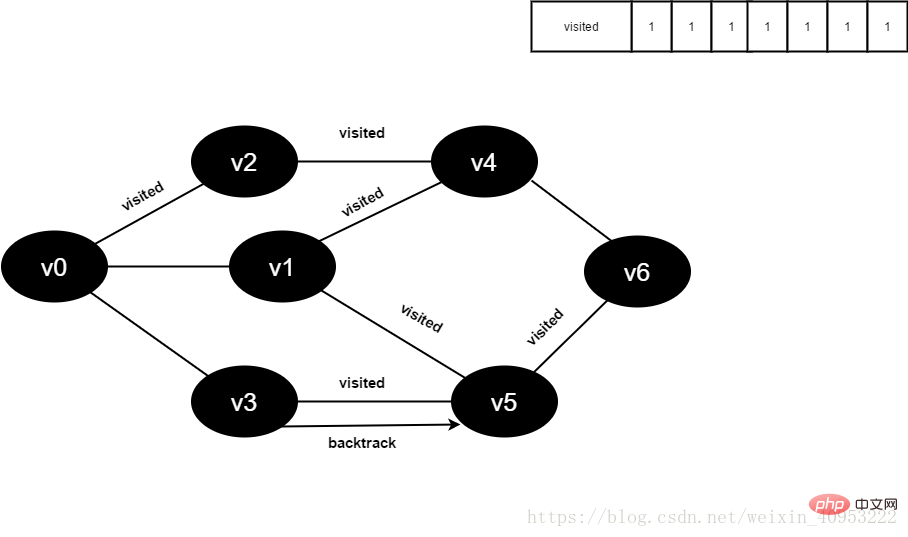
图4-2-15
16.访问v6的邻接点v4，判断visited[4]，其值为1，不访问。
访问v6的邻接点v5，判断visited[5]，其值为1，不访问。
v6所有邻接点均已被访问，回溯到其上一个顶点v5，遍历v5剩余邻接点。
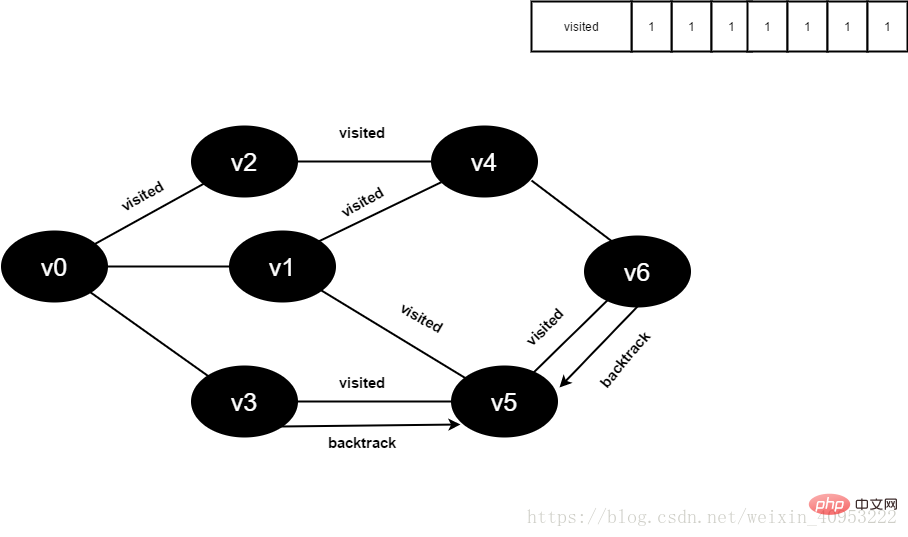
图4-2-16
17.v5所有邻接点均已被访问，回溯到其上一个顶点v1。
v1所有邻接点均已被访问，回溯到其上一个顶点v4，遍历v4剩余邻接点v6。
v4所有邻接点均已被访问，回溯到其上一个顶点v2。
v2所有邻接点均已被访问，回溯到其上一个顶点v1，遍历v1剩余邻接点v3。
v1所有邻接点均已被访问，搜索结束。
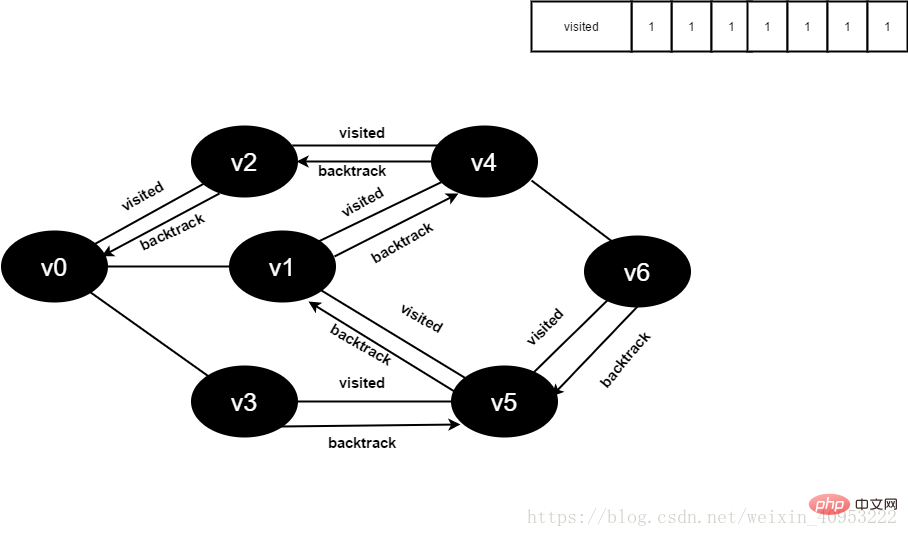
图4-2-17
邻接矩阵的创建在上述已描述过，这里不再赘述
void DFS_AM(AMGraph &G, int v)
{
int w;
printf("%c ", G.vexs[v]);
visited[v] = 1;
for (w = 0; w < G.vexnum; w++)
if (G.arcs[v][w]&&!visited[w]) //递归调用
DFS_AM(G,w);
}邻接表的创建在上述已描述过，这里不再赘述。
void DFS_AL(ALGraph &G, int v)
{
int w;
printf("%c ", G.vertices[v].data);
visited[v] = 1;
ArcNode *p = new ArcNode;
p = G.vertices[v].firstarc;
while (p)
{
w = p->adjvex;
if (!visited[w]) DFS_AL(G, w);
p = p->nextarc;
}
}更多相关知识，请访问：PHP中文网！
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Barre oblique du tableau Excel divisée en deux
Solution à une signature invalide
La différence entre python et pycharm
Quelles sont les applications de l'Internet des objets ?
que signifie l'élan
La différence entre a++ et ++a
Le rôle du Serverlet en Java
Qu'est-ce qui est mis en évidence dans jquery
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
