

Trier signifie organiser les éléments d'une liste linéaire dans un ordre spécifique (numérique ou alphabétique). Le tri est souvent utilisé conjointement avec la recherche.
Il existe de nombreux algorithmes de tri, et l'un des plus rapides est de loin le Quicksort .
Quicksort trie les éléments de la liste donnés en utilisant la stratégie diviser pour régner. Cela signifie que l'algorithme divise le problème en sous-problèmes jusqu'à ce que les sous-problèmes deviennent suffisamment simples pour être résolus directement.
Algorithmiquement, cela peut être réalisé en utilisant la récursivité ou le bouclage. Mais pour ce problème, il est plus naturel d’utiliser la récursivité.
Regardez d'abord comment fonctionne le tri rapide :
Ensuite, comprenez ces étapes à travers un exemple. Supposons que nous ayons un tableau avec des éléments non triés [7, -2, 4, 1, 6, 5, 0, -4, 2]. Sélectionnez le dernier élément comme base. Les étapes de décomposition du tableau sont présentées dans la figure ci-dessous :
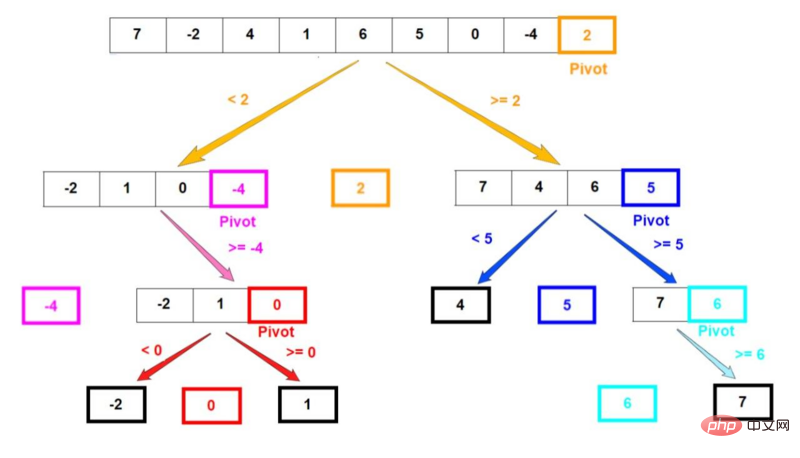
Les éléments sélectionnés comme base à l'étape 1 de l'algorithme sont colorés. Après le partitionnement, l'élément de base est toujours à la bonne position dans le tableau.
Le tableau avec une bordure noire en gras représente à quoi il ressemblera à la fin de cette branche de récursion particulière, le tableau résultant ne contenant qu'un seul élément.
Enfin vous pouvez voir le tri des résultats de l'algorithme.
L'épine dorsale de cet algorithme est l'étape de « partitionnement ». Qu'il s'agisse d'utiliser la récursion ou le bouclage, cette étape est la même.
C'est précisément à cause de cette fonctionnalité que le code de partitionnement de tableau est écrit en premier partition() :
function partition(arr, start, end){
// 以最后一个元素为基准
const pivotValue = arr[end];
let pivotIndex = start;
for (let i = start; i < end; i++) {
if (arr[i] < pivotValue) {
// 交换元素
[arr[i], arr[pivotIndex]] = [arr[pivotIndex], arr[i]];
// 移动到下一个元素
pivotIndex++;
}
}
// 把基准值放在中间
[arr[pivotIndex], arr[end]] = [arr[end], arr[pivotIndex]]
return pivotIndex;
};Le code utilise le dernier élément comme base et utilise la variable pivotIndex pour suivez la position "milieu", tous les éléments à gauche de cette position sont plus petits que pivotValue, tandis que tous les éléments à droite sont plus grands que pivotValue.
La dernière étape échange la base (dernier élément) avec pivotIndex.
Après avoir implémenté la fonction partition(), nous devons résoudre le problème de manière récursive et appliquer la logique de partitionnement pour terminer les étapes restantes :
function quickSortRecursive(arr, start, end) {
// 终止条件
if (start >= end) {
return;
}
// 返回 pivotIndex
let index = partition(arr, start, end);
// 将相同的逻辑递归地用于左右子数组
quickSort(arr, start, index - 1);
quickSort(arr, index + 1, end);
}Dans cette fonction Partitionnez d’abord le tableau, puis partitionnez les sous-tableaux gauche et droit. Tant que cette fonction reçoit un tableau qui n'est pas vide ou qui contient plusieurs éléments, le processus sera répété.
Les tableaux vides et les tableaux contenant un seul élément sont considérés comme triés.
Enfin, utilisez l'exemple suivant pour tester :
array = [7, -2, 4, 1, 6, 5, 0, -4, 2] quickSortRecursive(array, 0, array.length - 1) console.log(array)
Sortie :
-4,-2,0,1,2,4,5,6,7
La méthode récursive de tri rapide est plus intuitive. Mais utiliser des boucles pour implémenter un tri rapide est une question d’entretien relativement courante.
Comme la plupart des solutions de conversion récursive en boucle, la première chose qui vient à l'esprit est d'utiliser une pile pour simuler des appels récursifs. Cela vous permet de réutiliser une logique récursive familière et de l'utiliser dans des boucles.
Nous avons besoin d'un moyen de garder une trace des sous-tableaux non triés restants. Une approche consiste simplement à conserver des "paires" d'éléments sur la pile, représentant start et end pour un sous-tableau non trié donné.
JavaScript n'a pas de structure de données de pile explicite, mais les tableaux prennent en charge les fonctions push() et pop(). Mais la fonction peek() n'est pas prise en charge, vous devez donc utiliser stack [stack.length-1] pour vérifier manuellement le haut de la pile.
Nous utiliserons la même fonction de "partitionnement" que la méthode récursive. Jetez un œil à comment écrire la partie Quicksort :
function quickSortIterative(arr) {
// 用push()和pop()函数创建一个将作为栈使用的数组
stack = [];
// 将整个初始数组做为“未排序的子数组”
stack.push(0);
stack.push(arr.length - 1);
// 没有显式的peek()函数
// 只要存在未排序的子数组,就重复循环
while(stack[stack.length - 1] >= 0){
// 提取顶部未排序的子数组
end = stack.pop();
start = stack.pop();
pivotIndex = partition(arr, start, end);
// 如果基准的左侧有未排序的元素,
// 则将该子数组添加到栈中,以便稍后对其进行排序
if (pivotIndex - 1 > start){
stack.push(start);
stack.push(pivotIndex - 1);
}
// 如果基准的右侧有未排序的元素,
// 则将该子数组添加到栈中,以便稍后对其进行排序
if (pivotIndex + 1 < end){
stack.push(pivotIndex + 1);
stack.push(end);
}
}
}Voici le code du test :
ourArray = [7, -2, 4, 1, 6, 5, 0, -4, 2] quickSortIterative(ourArray) console.log(ourArray)
Sortie :
-4,-2,0,1,2,4,5,6,7
Quand En ce qui concerne les algorithmes de tri, les visualiser peut nous aider à comprendre intuitivement leur fonctionnement. L'exemple suivant est tiré de Wikipédia :
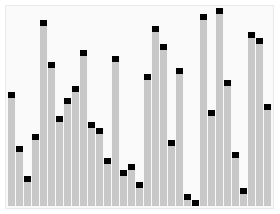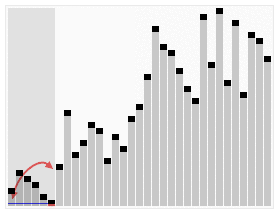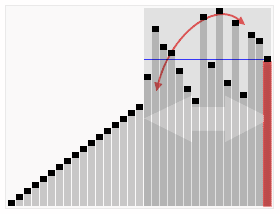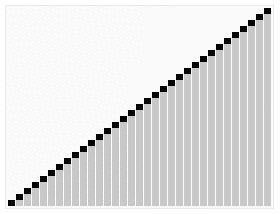
Le dernier élément de la figure est également utilisé comme élément. référence. Étant donné un tableau partitionné, parcourez récursivement le côté gauche jusqu'à ce qu'il soit complètement trié. Triez ensuite le côté droit.
Discutez maintenant de sa complexité temporelle et spatiale. La complexité temporelle dans le pire des cas du tri rapide est $O(n^2)$. La complexité temporelle moyenne est de $O(nlog n)$. En règle générale, les pires scénarios peuvent être évités en utilisant une version aléatoire du tri rapide.
La faiblesse de l'algorithme de tri rapide est le choix du benchmark. Chaque fois que vous choisissez un mauvais pivot (un pivot plus grand ou plus petit que la plupart des éléments), vous obtiendrez la pire complexité temporelle possible. Lors de la sélection répétée d'une base, la complexité temporelle est $O(nlog n)$ si la valeur de l'élément est inférieure ou supérieure à la base de l'élément.
On peut observer empiriquement que la complexité temporelle du tri rapide a tendance à avoir $O(nlog n)$ quelle que soit la stratégie de sélection de référence de données adoptée.
Quicksort ne prend aucun espace supplémentaire (hors espace réservé aux appels récursifs). Cet algorithme est appelé algorithme sur place et ne nécessite aucun espace supplémentaire.
Pour plus de connaissances sur la programmation, veuillez visiter : Introduction à la programmation ! !
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!