 base de données
base de données
 tutoriel mysql
tutoriel mysql
 Comprenez enfin que l'index MySQL doit utiliser B+tree, et c'est si rapide
Comprenez enfin que l'index MySQL doit utiliser B+tree, et c'est si rapide
Comprenez enfin que l'index MySQL doit utiliser B+tree, et c'est si rapide
La colonne
tutoriel mysql présente le B+tree pour comprendre les index.

Recommandation gratuite : tutoriel mysql(vidéo)
Avant-propos
Lorsque vous rencontrez un SQL lent et que vous devez l'optimiser, quelle est la première méthode d'optimisation à laquelle vous pouvez penser ?
La première réaction de la plupart des gens peut être d'ajouter un index Dans la plupart des cas, index peut améliorer l'efficacité des requêtes d'une instruction SQL de plusieurs fois <.>Ordre de grandeur.
essence d'un index : une structure de données utilisée pour retrouver rapidement des enregistrements.
Structures de données couramment utilisées pour les index :
- Arbre binaire
- Arbre rouge-noir
- Table de hachage
- (L'arbre B n'est pas appelé arbre B-soustrait)
B-tree B+tree
Structure graphique des donnéesSite Web : https : // www.cs.usfca.edu/~galles/visualization/Algorithms.html
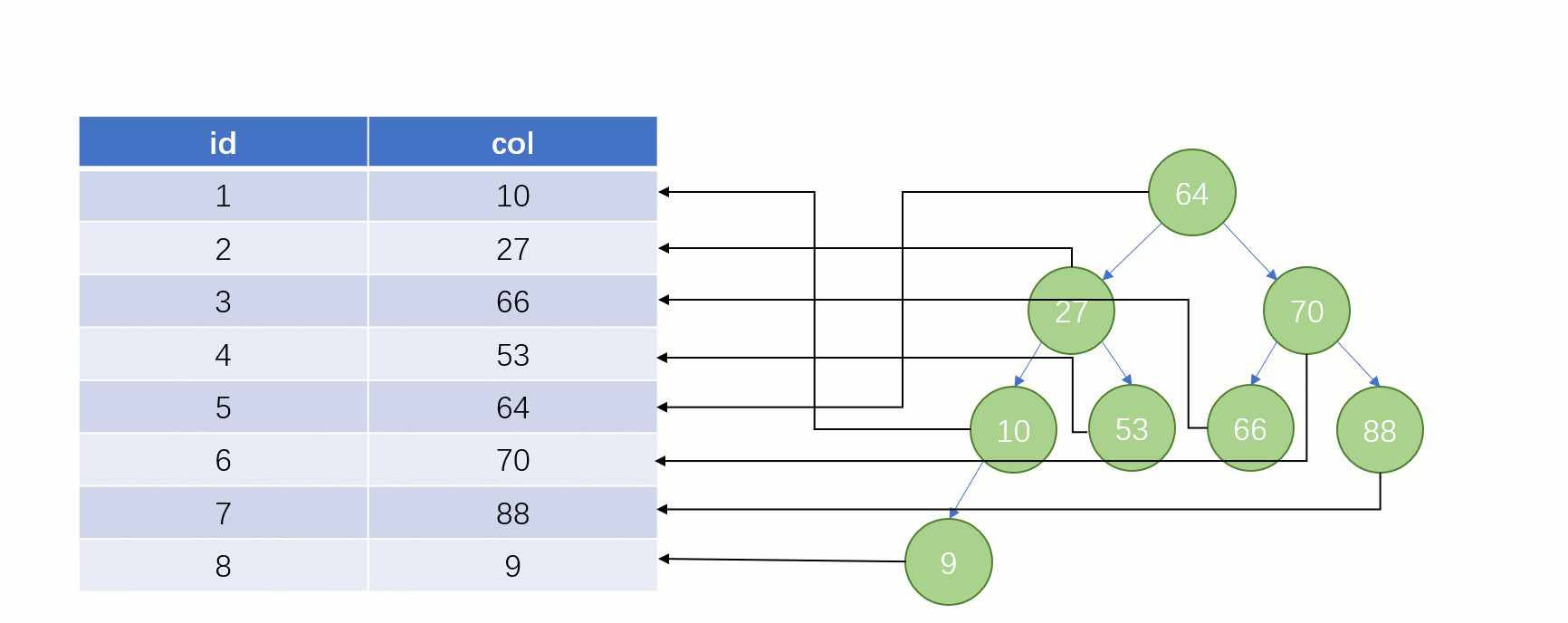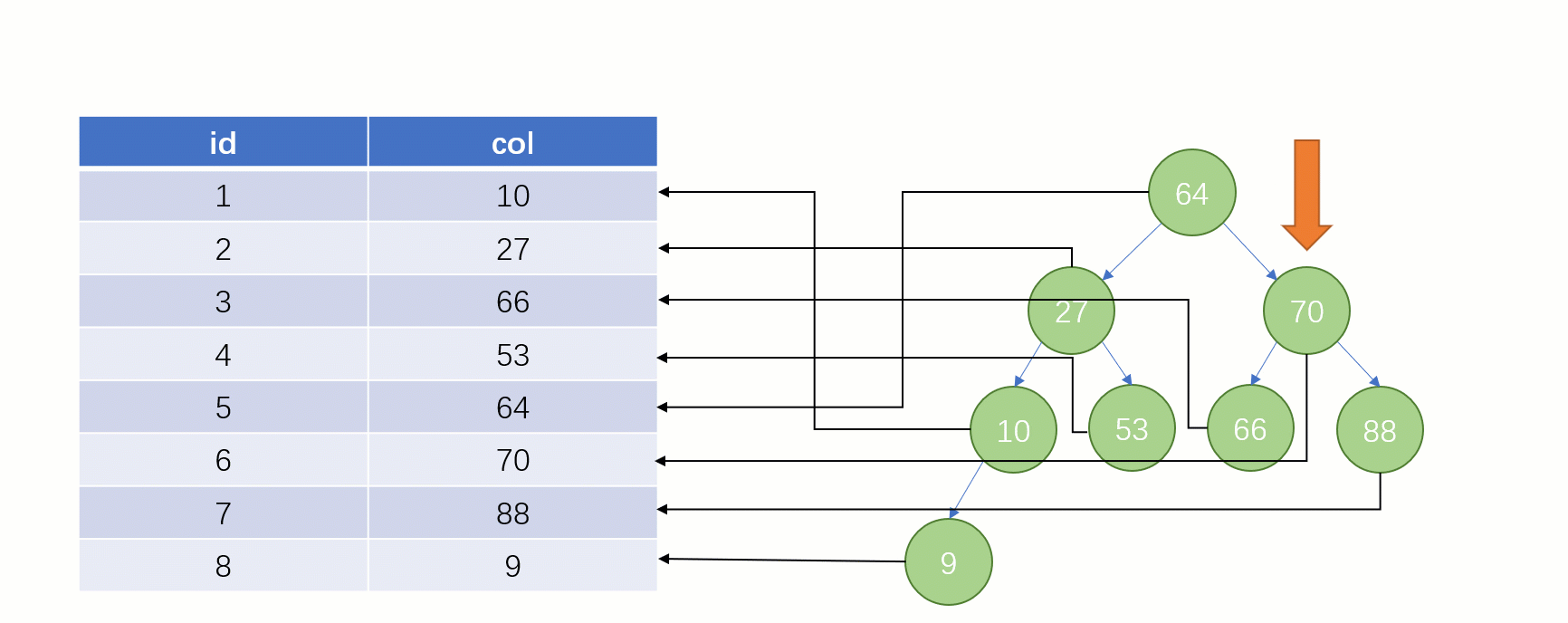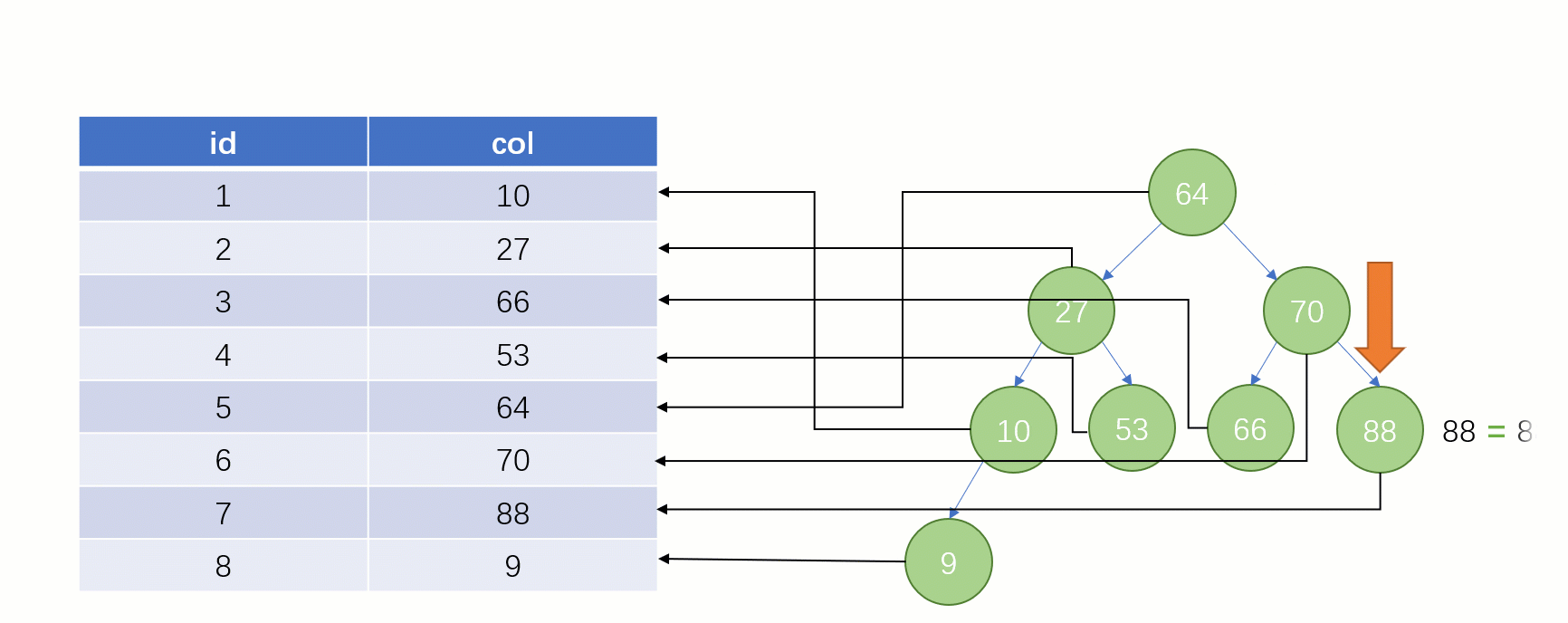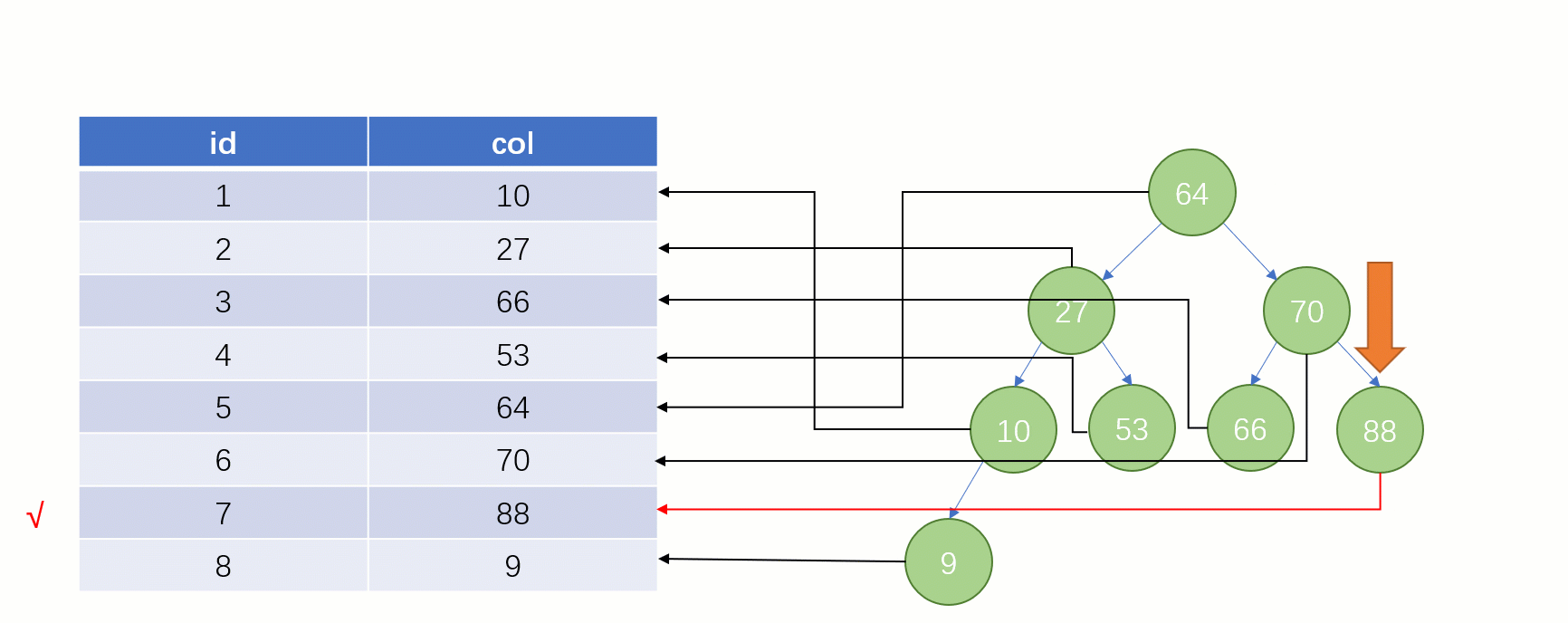
Requête d'indexTout le monde sait que une telle select * from t where col = 88 déclaration sera normale si elle est recherché sans utiliser l'index. La recherche locale est une SQLanalyse complète du tableau : en commençant par la première ligne du tableau, en recherchant ligne par ligne et en comparant la valeur du champ de chaque ligne avec 88col. C'est évidemment très faible.
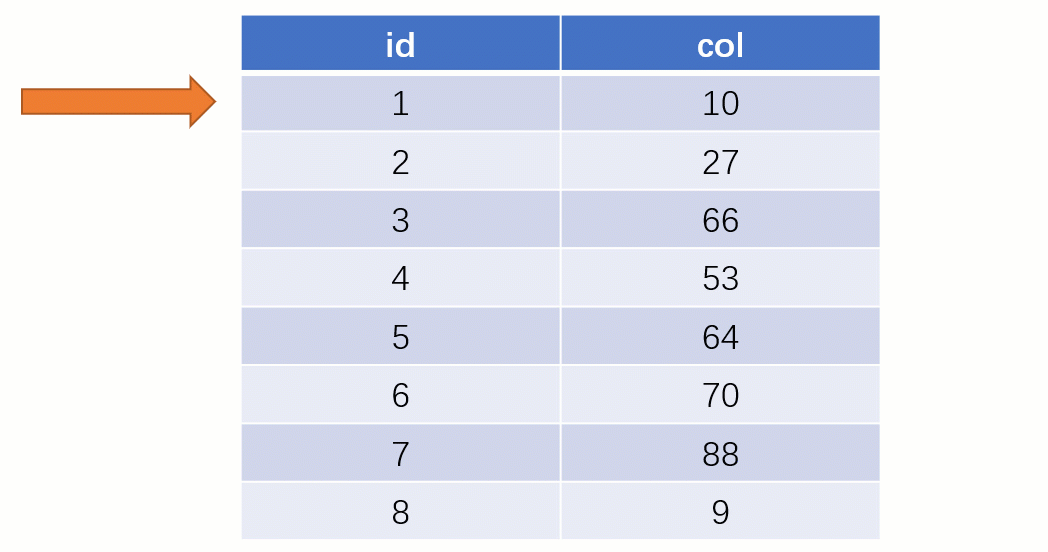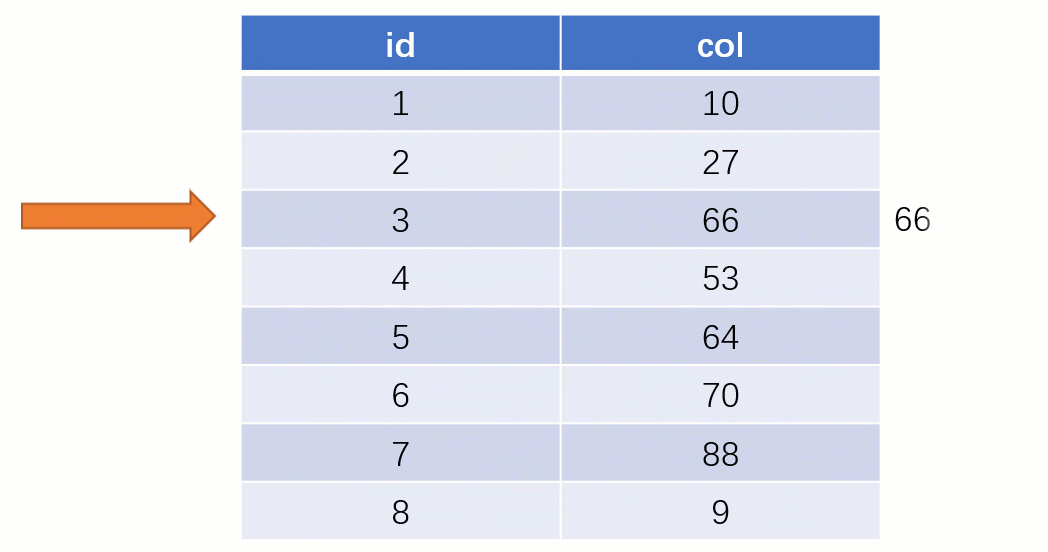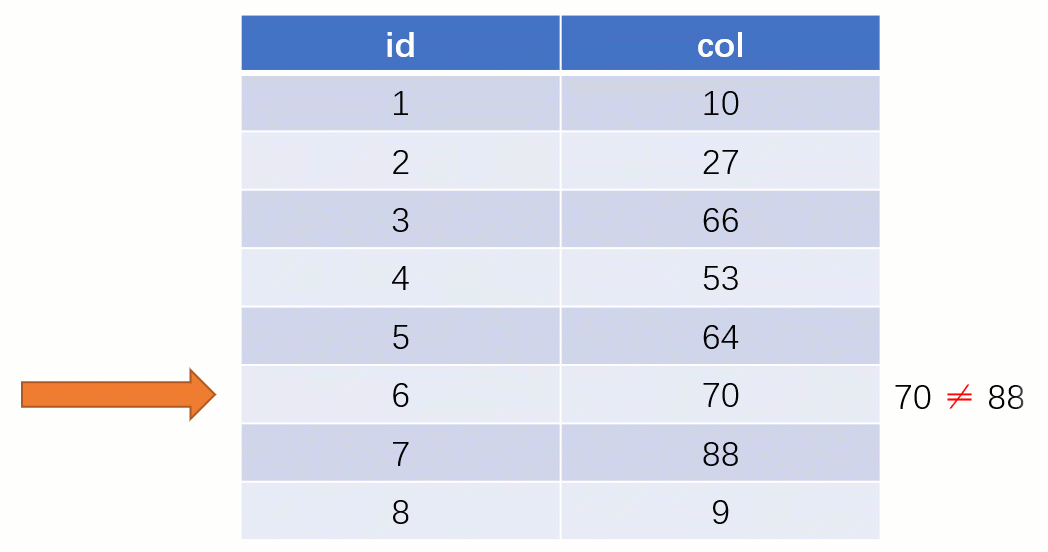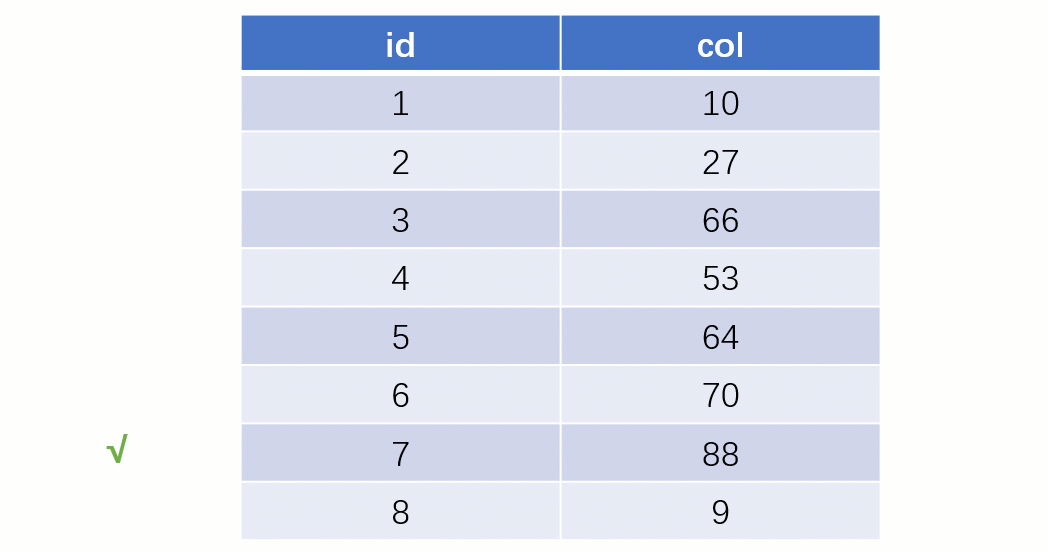 Si vous utilisez un index, le processus de requête est complètement différent (en supposant qu'une structure de données
Si vous utilisez un index, le processus de requête est complètement différent (en supposant qu'une structure de données
est utilisée pour stocker nos colonnes d'index) La structure de stockage de l'arborescence binaire à ce moment (Clé - Valeur) : La clé est les données du champ d'index et la valeur est l'adresse du fichier disque de la ligne où se trouve l'index.
Lorsque vous trouvez enfin
88, vous pouvez retirer l'adresse du fichier disque correspondant à sa valeur, puis accéder directement au disque pour trouver cette ligne de données La vitesse à ce moment. Ce sera beaucoup plus rapide qu’une analyse complète de la table.
 Mais
Mais
la couche inférieure n'utilise pas arbre binaireMySQL pour stocker les données d'index, mais utilise B +arbre (B+arbre) . Pourquoi ne pas utiliser un arbre binaire
En supposant qu'un arbre binaire ordinaire soit utilisé pour enregistrer la colonne d'index
, nous devons conserver le champ d'index de l'arbre binaire lors de l'insertion d'une ligne d'enregistrements.id
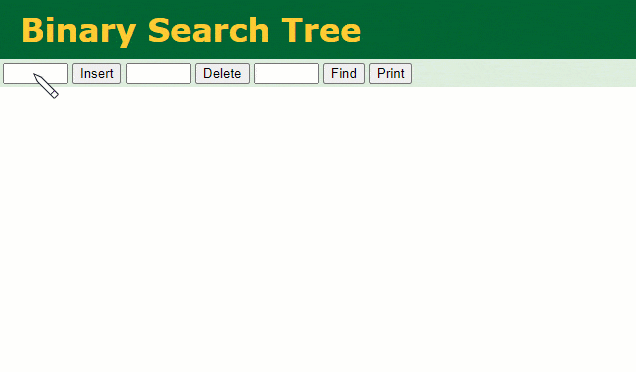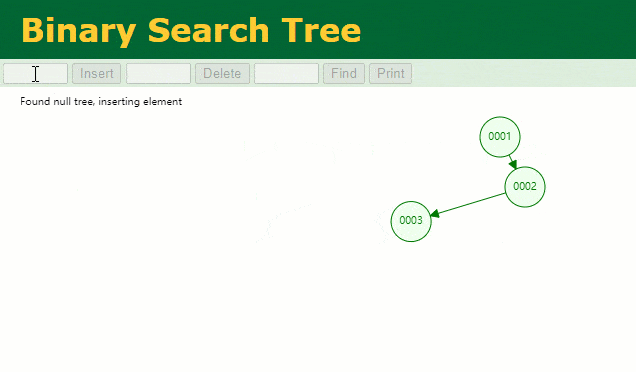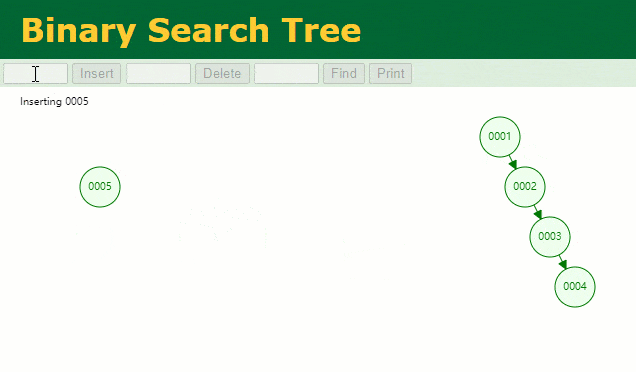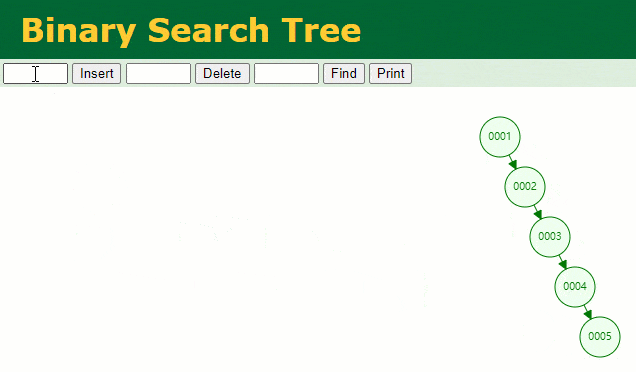 Lorsque je souhaite retrouver les données de
Lorsque je souhaite retrouver les données de
id = 7
 À cette fois, la ligne
À cette fois, la ligne
7id = 7 fois, ce qui n'est pas très différent de notre analyse complète de la table. De toute évidence, l'arbre binaire est en fait une structure de données qui ne convient pas à pour être utilisée comme index pour ce type de colonnes de données dans lesquelles augmente séquentiellement . Pourquoi ne pas utiliser la table de hachage
, nous devons conserver l'index de la table de hachage lors de l'insertion de chaque ligne d'enregistrements. champ.Fonction de hachage : convertir un Any Le type de clé peut être converti en indice de type int
En supposant que la table de hachage est utilisée pour enregistrer la colonne d'index
id
 À cette époque, le nœud d'arbre de
À cette époque, le nœud d'arbre de
1id = 7 fois, ce qui est très efficace.
 Mais l'index de
Mais l'index de
n'utilise pas la MySQLTable de hachage qui peut être positionnée avec précision. Parce que cela ne s'applique pas aux requêtes de plage. Pourquoi ne pas utiliser l'arbre rouge-noir
L'arbre rouge-noir est un arbre AVL spécialisé (arbre binaire équilibré), qui est maintenu par des opérations spécifiques lors des opérations d'insertion et de suppression. d'arbres de recherche binaires ;
Si un arbre de recherche binaire est un arbre rouge-noir, alors n'importe lequel de ses sous-arbres doit être un arbre rouge-noir.
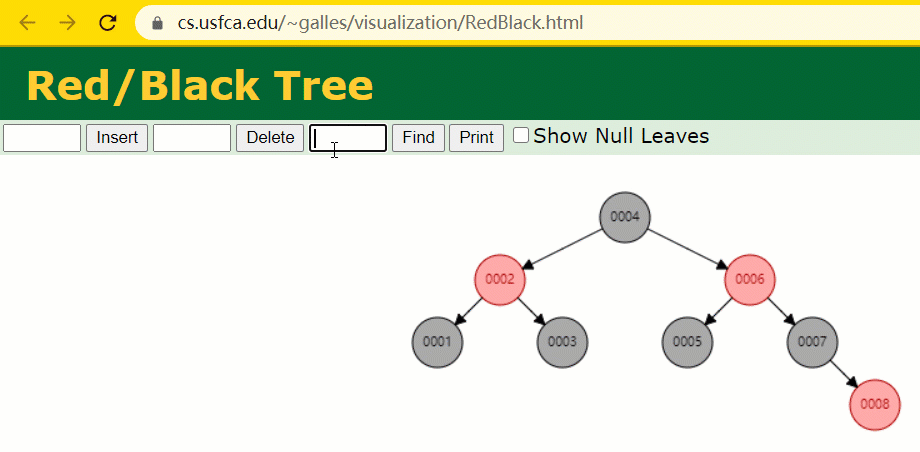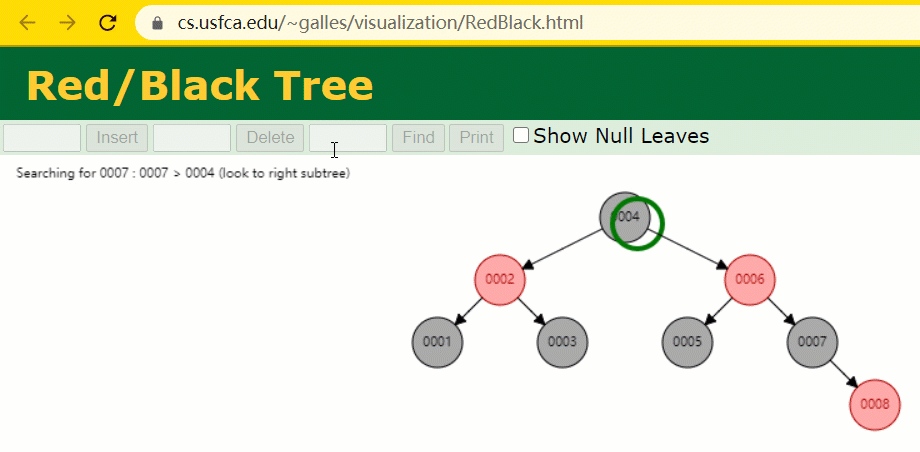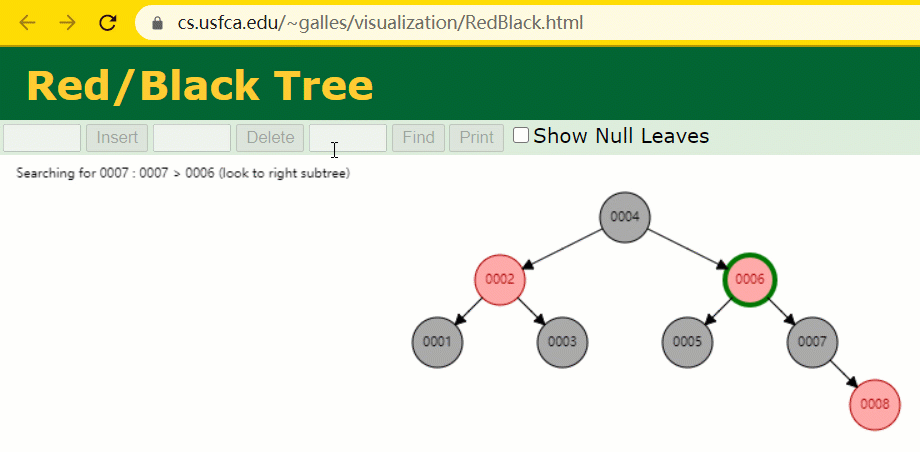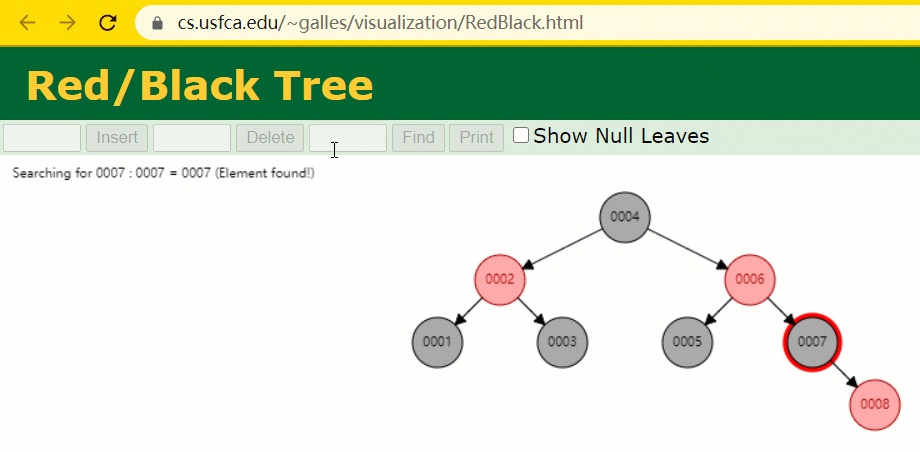
En supposant que l'arbre rouge-noir est utilisé pour enregistrer la colonne d'index id, nous devons conserver le champ d'index de l'arbre rouge-noir lors de l'insertion d'une ligne d'enregistrements.

Pendant le processus d'insertion, vous constaterez qu'il est différent des arbres binaires ordinaires en ce sens que lorsque la différence de hauteur entre les sous-arbres gauche et droit d'un arbre est > 1, il effectuera une rotation opération pour maintenir l'arbre en équilibre.
À cette époque, le nœud de l'arbre de id = 7 n'a été recherché que 3 fois, ce qui est toujours plus rapide que l'arbre binaire dit ordinaire.
Mais l'indice de MySQL toujours n'utilise pas arbre rouge-noir qui est excellent en termes de positionnement et de portée précis requête.
Parce que lorsque MySQL la quantité de données est importante, la taille de l'index sera également très grande et pourra ne pas être stockée dans la mémoire, la lecture et l'écriture associées doivent donc être effectuées à partir du disque. Si le niveau de l'arborescence est trop élevé, alors lecture. Plus il y aura d'écritures sur disque (interactions E/S), plus les performances seront mauvaises.
Arbre B
Le seul défaut de l'arbre rouge-noir actuellement est que la hauteur de l'arbre est incontrôlable, alors maintenant notre point d'entrée est l'arbre La hauteur de .
Actuellement, un nœud n'est alloué que pour stocker 1 élément. Si nous voulons contrôler la hauteur, nous pouvons allouer un espace plus grand à un nœud et le laisser stocker plusieurs éléments horizontalement, à cette fois, la hauteur est contrôlable. Grâce à un tel processus de transformation, il devient
B-tree.
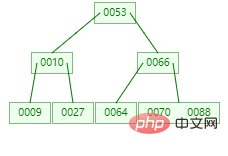
B-tree est un arbre multivoies absolument équilibré. Il y a deux concepts dans sa structure
Degré : le nombre de nœuds enfants (sous-arbres) qu'un nœud possède. (À certains endroits, est expliqué en termes de degré
B-tree, veuillez expliquer ici)ordre : le nombre maximum de nœuds enfants d'un nœud. (Généralement représenté par m)
Mot clé : Index de données.
Un ordre m B-tree est un arbre de recherche m-way équilibré. Il peut s'agir d'un arbre vide, ou répondre aux caractéristiques suivantes :
-
À l'exception du nœud racine et du nœud feuille, tout autre nœud a au moins nœud enfant
vaut m/2 puis arrondi à l'entier supérieur
Le nombre j de mots-clés contenus dans chaque nœud non racine satisfait : - 1 ≤ j ≤ m - 1;
Les mots-clés du nœud sont classés par ordre croissant de gauche à droite. Un nœud non-feuille avec k mots-clés a exactement (k + 1) nœuds enfants
-
Tous les nœuds feuilles sont situés sur le même calque.
Signification du nom (hors sujet, détendez-vous)
Ce qui suit est tiré de Wikipédia
Rudolf Bayer ( Rudolf Bayer et Ed M. McCreight a inventé B-tree en 1972 alors qu'il travaillait aux laboratoires de recherche de Boeing, mais ils n'ont pas expliqué ce que signifiait le B, le cas échéant.
Douglas Comer explique : Aucun des deux auteurs n'a jamais expliqué le sens original de B-tree. Nous pourrions penser qu’un texte équilibré, large ou touffu pourrait être approprié. D'autres ont suggéré que la lettre B signifiait Boeing. Cependant, en raison de son parrainage, il semble plus approprié de considérer B-tree comme un arbre Bayer.
Donald Knuth a spéculé sur la signification du nom B-tree dans son article intitulé "Conférence en classe CS144C sur le stockage sur disque et les arbres B" publié en mai 1980 et a proposé que B puisse signifier le nom de Boeing ou de Bayer. La recherche de
B-tree est en fait très similaire à un arbre binaire :
Un arbre binaire a un mot-clé et deux branches sur chaque nœud, et chaque nœud sur B-tree Les nœuds ont k mots-clés et (k + 1) branches.
La recherche par arbre binaire considère uniquement s'il faut aller à gauche ou à droite, tandis que B-tree doit être déterminée par plusieurs branches. La recherche de
B-tree est divisée en deux étapes :
- Recherchez d'abord le nœud. Puisque
B-treeest généralement stocké sur le disque, cette étape nécessite une opération disk IO - lorsqu'un certain après. le nœud, le nœud est lu dans la mémoire puis le mot-clé est trouvé par recherche séquentielle ou binaire. Si le mot-clé n'est pas trouvé, vous devez juger de la taille pour trouver une branche appropriée pour continuer la recherche.
Processus de fonctionnement
Vous devez maintenant trouver les éléments : 88
Première fois : Disque IO

La deuxième fois : Disque IO

La troisième fois : Disque IO
Ensuite, il y a une comparaison de mémoire, qui est comparée respectivement à 70 et 88. Finalement 88 trouvés.

D'après le processus de recherche, nous avons constaté que B-tree le nombre de comparaisons et le nombre d'E/S de disque ne sont en fait pas très différents de ceux des arbres binaires. il n'y a aucun avantage.
Mais si vous regardez attentivement, vous constaterez que la comparaison est effectuée en mémoire, n'implique pas d'E/S disque et la consommation de temps est négligeable.
De plus, un nœud dans B-tree peut stocker de nombreux mots-clés (le nombre est déterminé par la commande), et le même nombre de mots-clés peut être stocké dans B-tree Les nœuds générés sont bien inférieurs aux nœuds de l'arborescence binaire, et la différence dans le nombre de nœuds est équivalente au nombre d'E/S disque. Après avoir atteint un certain nombre, la différence de performances devient apparente.
Insérer
Lorsque B-tree souhaite insérer un mot-clé, il trouve directement le nœud feuille et effectue l'opération.
- Trouver le nœud feuille à insérer en fonction du mot-clé à insérer
- car le nombre maximum (ordre) de nœuds enfants d'un nœud est m , il faut donc déterminer si le nombre de mots-clés dans le nœud actuel est inférieur à (m - 1).
- Oui : insérer directement
- Non : La division du nœud se produit, divisez le nœud en parties gauche et droite en fonction du mot-clé du milieu du nœud et placez le mot-clé du milieu into Accédez simplement au nœud parent.
Processus de fonctionnement
Par exemple, nous devons maintenant insérer des éléments dans B-tree avec un degré maximum (ordre) de 3 : 72
-
Trouver le nœud feuille à insérer

Répartition du nœud : il doit être sur le même bloc de disque que [70 ,88], Mais lorsqu'un nœud a 3 mots-clés, il peut avoir 4 nœuds enfants, ce qui dépasse le degré maximum 3 de la limite que nous avons définie, donc à ce moment le fractionnement doit être effectué : avec le mot-clé du milieu Divisez le nœud en deux pour la limite, générez un nouveau nœud et déplacez le mot-clé du milieu vers le nœud parent.

Astuce : Lorsqu'il y a deux mots-clés du milieu, le mot-clé de gauche est généralement utilisé. Monter la scission.
Supprimer
L'opération de suppression est plus gênante que la recherche et l'insertion, car le mot-clé à supprimer peut ou non être sur le nœud feuille, et la suppression peut également provoquer B-tree Si le L'arbre est déséquilibré, des opérations telles que la fusion et la rotation doivent être effectuées pour maintenir l'équilibre de l'arbre entier.
Prenons simplement un arbre (niveau 5) comme exemple
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Compétences de traitement de structures de données volumineuses de PHP
May 08, 2024 am 10:24 AM
Compétences de traitement de structures de données volumineuses de PHP
May 08, 2024 am 10:24 AM
Compétences en matière de traitement de la structure des Big Data : Chunking : décomposez l'ensemble de données et traitez-le en morceaux pour réduire la consommation de mémoire. Générateur : générez des éléments de données un par un sans charger l'intégralité de l'ensemble de données, adapté à des ensembles de données illimités. Streaming : lisez des fichiers ou interrogez les résultats ligne par ligne, adapté aux fichiers volumineux ou aux données distantes. Stockage externe : pour les ensembles de données très volumineux, stockez les données dans une base de données ou NoSQL.
 Comment optimiser les performances des requêtes MySQL en PHP ?
Jun 03, 2024 pm 08:11 PM
Comment optimiser les performances des requêtes MySQL en PHP ?
Jun 03, 2024 pm 08:11 PM
Les performances des requêtes MySQL peuvent être optimisées en créant des index qui réduisent le temps de recherche d'une complexité linéaire à une complexité logarithmique. Utilisez PreparedStatements pour empêcher l’injection SQL et améliorer les performances des requêtes. Limitez les résultats des requêtes et réduisez la quantité de données traitées par le serveur. Optimisez les requêtes de jointure, notamment en utilisant des types de jointure appropriés, en créant des index et en envisageant l'utilisation de sous-requêtes. Analyser les requêtes pour identifier les goulots d'étranglement ; utiliser la mise en cache pour réduire la charge de la base de données ; optimiser le code PHP afin de minimiser les frais généraux.
 Comment utiliser la sauvegarde et la restauration MySQL en PHP ?
Jun 03, 2024 pm 12:19 PM
Comment utiliser la sauvegarde et la restauration MySQL en PHP ?
Jun 03, 2024 pm 12:19 PM
La sauvegarde et la restauration d'une base de données MySQL en PHP peuvent être réalisées en suivant ces étapes : Sauvegarder la base de données : Utilisez la commande mysqldump pour vider la base de données dans un fichier SQL. Restaurer la base de données : utilisez la commande mysql pour restaurer la base de données à partir de fichiers SQL.
 Comment insérer des données dans une table MySQL en utilisant PHP ?
Jun 02, 2024 pm 02:26 PM
Comment insérer des données dans une table MySQL en utilisant PHP ?
Jun 02, 2024 pm 02:26 PM
Comment insérer des données dans une table MySQL ? Connectez-vous à la base de données : utilisez mysqli pour établir une connexion à la base de données. Préparez la requête SQL : Écrivez une instruction INSERT pour spécifier les colonnes et les valeurs à insérer. Exécuter la requête : utilisez la méthode query() pour exécuter la requête d'insertion en cas de succès, un message de confirmation sera généré.
 Comment corriger les erreurs mysql_native_password non chargé sur MySQL 8.4
Dec 09, 2024 am 11:42 AM
Comment corriger les erreurs mysql_native_password non chargé sur MySQL 8.4
Dec 09, 2024 am 11:42 AM
L'un des changements majeurs introduits dans MySQL 8.4 (la dernière version LTS en 2024) est que le plugin « MySQL Native Password » n'est plus activé par défaut. De plus, MySQL 9.0 supprime complètement ce plugin. Ce changement affecte PHP et d'autres applications
 Comment utiliser les procédures stockées MySQL en PHP ?
Jun 02, 2024 pm 02:13 PM
Comment utiliser les procédures stockées MySQL en PHP ?
Jun 02, 2024 pm 02:13 PM
Pour utiliser les procédures stockées MySQL en PHP : Utilisez PDO ou l'extension MySQLi pour vous connecter à une base de données MySQL. Préparez l'instruction pour appeler la procédure stockée. Exécutez la procédure stockée. Traitez le jeu de résultats (si la procédure stockée renvoie des résultats). Fermez la connexion à la base de données.
 Comment créer une table MySQL en utilisant PHP ?
Jun 04, 2024 pm 01:57 PM
Comment créer une table MySQL en utilisant PHP ?
Jun 04, 2024 pm 01:57 PM
La création d'une table MySQL à l'aide de PHP nécessite les étapes suivantes : Connectez-vous à la base de données. Créez la base de données si elle n'existe pas. Sélectionnez une base de données. Créer un tableau. Exécutez la requête. Fermez la connexion.
 La différence entre la base de données Oracle et MySQL
May 10, 2024 am 01:54 AM
La différence entre la base de données Oracle et MySQL
May 10, 2024 am 01:54 AM
La base de données Oracle et MySQL sont toutes deux des bases de données basées sur le modèle relationnel, mais Oracle est supérieur en termes de compatibilité, d'évolutivité, de types de données et de sécurité ; tandis que MySQL se concentre sur la vitesse et la flexibilité et est plus adapté aux ensembles de données de petite et moyenne taille. ① Oracle propose une large gamme de types de données, ② fournit des fonctionnalités de sécurité avancées, ③ convient aux applications de niveau entreprise ; ① MySQL prend en charge les types de données NoSQL, ② a moins de mesures de sécurité et ③ convient aux applications de petite et moyenne taille.






