entretien java - structure des données

Les structures de données courantes incluent : entretien java - structure des données, Hashtable, Concurrententretien java - structure des données.

(Partage de vidéos associées : vidéo d'enseignement Java)

Présentons-les séparément :

entretien java - structure des données

• Implémentation sous-jacente : la structure globale sous-jacente de entretien java - structure des données est un tableau, et chaque élément du tableau est une liste chaînée. Chaque fois qu'un objet (put) est ajouté, un objet de liste chaînée (type d'objet) sera généré. Chaque entrée dans la carte est un élément du tableau (Map.Entry est un <key></key>), qui pointe vers l'élément actuel. au suivant Les références aux éléments forment une liste chaînée.
• Principe de stockage : lors de l'ajout d'un élément à HsahMap, calculez d'abord la valeur de hachage de l'objet Key et récupérez l'indice du tableau. Si la position dans le tableau est vide, insérez-la, sinon parcourez la liste chaînée à cet endroit. position. Lorsque l'objet Key et l'objet Node d'un nœud sont égaux au nouvel élément, remplacez l'objet Value du nœud par l'objet Value du nouvel élément, sinon insérez un nouveau nœud. (Remarque : Des arbres rouge-noir ont été ajoutés après JDK 8)

La longueur de entretien java - structure des données est de 2 élevée à la nième puissance afin de rendre tous les bits du la valeur binaire de length-1 complete est 1. Dans ce cas, lorsque la valeur de hachage et (table.length - 1) effectuent une opération & pour calculer l'index, le résultat est équivalent à la valeur des derniers chiffres du hashcode. À ce stade, tant que le hashcode d'entrée lui-même est distribué uniformément, l'algorithme de hachage Le résultat est l'uniformité. Par conséquent, la longueur par défaut de entretien java - structure des données est de 16 pour réduire la probabilité de collision de hachage, et c'est également une taille appropriée.

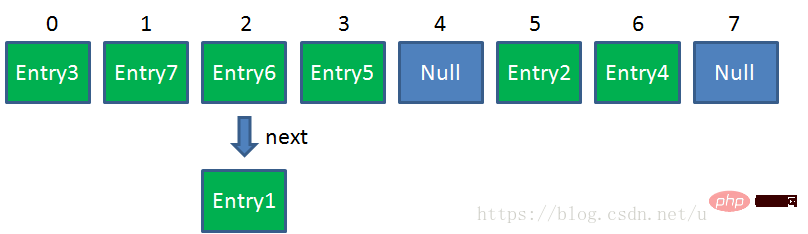
Table de hachage

比较点	entretien java - structure des données	Hashtable
实现原理	见上小节	和entretien java - structure des données的实现原理几乎一样
Key和Value	允许Key和Value为null	不允许Key和Value为null
扩容策略	2倍扩容oldThr	2倍+1扩容(oldCapacity
安全性	线程不安全	线程安全

La stratégie de sécurité des threads de la table de hachage est très coûteuse à mettre en œuvre. Toutes les opérations get/put associées sont synchronisées et les performances sont très médiocres dans des scénarios de concurrence hautement compétitifs.

Concurrententretien java - structure des données

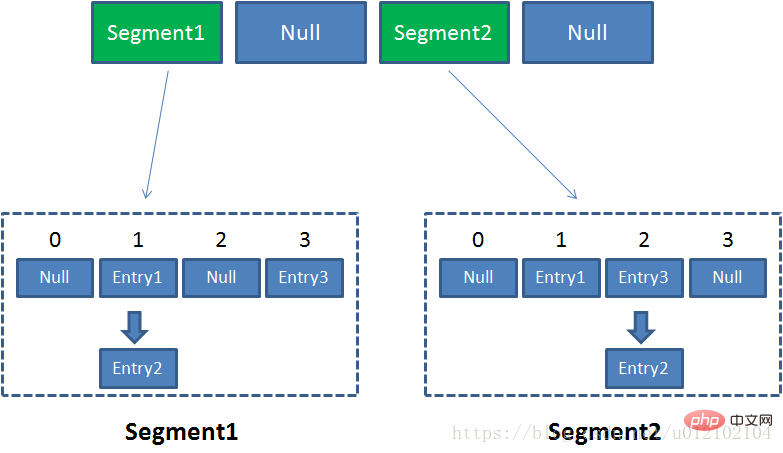
Concurrententretien java - structure des données est une implémentation entretien java - structure des données thread-safe et efficace fournie dans le package de concurrence Java. Elle adopte une stratégie de verrouillage de segmentation très exquise. de Concurrententretien java - structure des données est le tableau Segment. Le segment hérite de ReentrantLock et est un verrou réentrant. Chaque segment est une sous-table de hachage et un tableau HashEntry est conservé dans le segment. Dans un environnement simultané, il n'est pas nécessaire de prendre en compte la concurrence des verrous lors de l'exploitation des données de différents segments.

Linkedentretien java - structure des données, TreeMap, TreeSet

• Linkedentretien java - structure des données : entretien java - structure des données à accès séquentiel (implémenté sur la base de tableaux et de listes doublement chaînées).
• TreeMap : tri interne (basé sur l'implémentation d'un arbre rouge-noir).
• TreeSet : une collection Set ordonnée (basée sur l'implémentation d'un arbre binaire).

ArrayList, LinkedList, Vector

• ArrayList : tableau dynamique (basé sur l'implémentation du tableau).
• LinkedList : tableau ordonné (implémenté sur la base d'une liste doublement chaînée).
• Vector : Conteneur d'objets, qui peut mettre des objets de différents types (implémentés en fonction de tableaux).

Collection et collections

• Collection : L'interface supérieure de la classe collection, les sous-interfaces incluent principalement List, Set, Queue, etc.
• Collections : fournit des classes d'outils pour les opérations de recherche, de tri, de remplacement et de sécurité des threads sur les collections.

(Recommandations pour des questions d'entretien plus connexes : questions et réponses d'entretien Java)

Arbre binaire

Concepts courants d'arbre binaire

• Arbre B+ : voir section base de donnéeshttps://blog.csdn.net/u012102104/article/details/79773362

• Arbre binaire équilibré (arbre AVL) : la valeur absolue de la différence de profondeur entre les sous-arbres gauche et droit de chaque nœud ne dépasse pas 1.

• Arbre de Huffman : L'arbre binaire avec la plus petite longueur de chemin pondérée est appelé l'arbre binaire optimal. La construction de l’arbre de Huffman n’est pas unique, mais la somme des longueurs de chemin pondérées de tous les nœuds feuilles est la plus petite.

• Arbre rouge-noir : un arbre de recherche binaire auto-équilibré, ses propriétés sont :

  1. Les nœuds sont rouges ou noirs.
  2. Le nœud racine est noir.
  3. Chaque nœud feuille est un nœud noir vide (nœud NIL).
  4. Les deux nœuds enfants de chaque nœud rouge sont noirs.
  5. Tous les chemins d'un nœud à chacune de ses feuilles contiennent le même nombre de nœuds noirs.

  Il ne peut pas y avoir deux nœuds rouges consécutifs sur tous les chemins de chaque feuille à la racine

Parcours d'arbre binaire

// 1. 先序遍历算法 DLRvoid Preorder ( BinTree bt ) {
	if ( bt ) {
		visit ( bt->data );
		Preorder ( bt->lchild );
		Preorder ( bt->rchild );
	}}// 2. 中序遍历算法 LDRvoid Inorder ( BinTree bt ) {
	if ( bt ) {
		Inorder ( bt->lchild );
		visit ( bt->data );
		Inorder ( bt->rchild );
	}}// 3. 后序遍历 LRDvoid Postorder ( BinTree bt ) {
	if ( bt ) {
		Postorder ( bt->lchild );
		Postorder ( bt->rchild );
		visit ( bt->data );
	}}// 4. 按层次遍历。/* 思路：利用一个队列，首先将根（头指针）入队列，以后若队列不空则取队头元素 p，
如果 p 不空，则访问之，然后将其左右子树入队列，如此循环直到队列为空。*/void LevelOrder ( BinTree bt ) {
	// 队列初始化为空
	InitQueue ( Q );
	// 根入队列
	EnQueue ( Q, bt );
	// 队列不空则继续遍历
	while ( ! QueueEmpty(Q) ) {
		DeQueue ( Q, p );
		if ( p!=NULL ) {
			visit ( p->data );
			// 左、右子树入队列
			EnQueue ( Q, p->lchild );
			EnQueue ( Q, p->rchild );
		}
	}}// 非递归遍历二叉树一般借助栈实现

Recommandations associées : Tutoriel d'introduction à Java

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!