Quelle est la complexité temporelle d'un programme utilisant l'algorithme de recherche binaire ?

La complexité temporelle d'un programme utilisant l'algorithme de recherche binaire est le "niveau logarithmique". La recherche binaire est une méthode de recherche très efficace. La complexité de l'algorithme est le nombre de boucles while, et la complexité temporelle peut être exprimée par « O(h)=O(log2n) ».

L'environnement d'exploitation de ce tutoriel : système Windows 7, ordinateur Dell G3.

La complexité temporelle d'un programme utilisant l'algorithme de recherche binaire est de "niveau logarithmique".

Recommandations associées : "Apprentissage en programmation"

La recherche binaire est également appelée recherche binaire, qui est une méthode de recherche plus efficace. Cependant, la recherche binaire nécessite que le tableau linéaire adopte une structure de stockage séquentielle et que les éléments du tableau soient classés par mots-clés.

Processus de recherche :

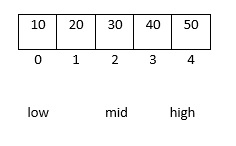
Tout d'abord, en supposant que les éléments du tableau sont classés par ordre croissant, comparez le mot-clé enregistré au milieu du tableau avec le mot-clé de recherche , s'ils sont égaux, alors la recherche est réussie ; sinon, l'enregistrement de la position médiane est utilisé pour diviser le tableau en sous-tableaux avant et dernier. Si le mot-clé enregistré en position médiane est supérieur au mot-clé de recherche, le précédent. la sous-table fait l'objet d'une recherche plus approfondie, sinon la dernière sous-table fait l'objet d'une recherche plus approfondie. Répétez le processus ci-dessus jusqu'à ce qu'un enregistrement répondant aux conditions soit trouvé, ce qui rend la recherche réussie, ou jusqu'à ce que la sous-table n'existe plus, auquel cas la recherche échoue.

Complexité de l'algorithme :

L'idée de base de la recherche binaire est de diviser n éléments en deux parties à peu près égales et de comparer a[n/2] avec x , si x=a[n/2], alors x est trouvé et l'algorithme se termine si xa [n/2] , puis recherchez simplement x dans la moitié droite du tableau a.

La complexité temporelle est le nombre de boucles while.

Il y a n éléments au total,

suit progressivement n, n/2, n/4,....n/2^k (le nombre d'éléments restant sera exploité ensuite ), où k est le nombre de cycles

Puisque votre n/2^k est arrondi >=1

c'est-à-dire n/2^k=1

peut être obtenu k=log2n, (c'est le logarithme de n avec base 2 comme base)

Donc la complexité temporelle peut être exprimée comme O(h)=O(log2n)

Ce qui suit fournit un pseudo-code pour l'implémentation de la recherche binaire :

BinarySearch(max,min,des)
mid-<(max+min)/2
while(min<=max)
mid=(min+max)/2
if mid=des then
return mid
elseif mid >des then
max=mid-1
else
min=mid+1
return max

La méthode de recherche binaire est également appelée méthode de recherche binaire. Elle utilise pleinement la relation d'ordre entre les éléments et adopte la stratégie diviser pour régner. avec O(log n) dans le pire des cas. Son idée de base est la suivante : (en supposant que les éléments du tableau sont classés par ordre croissant) divisez n éléments en deux moitiés avec à peu près le même nombre, prenez a[n/2] et comparez-le avec le x que vous voulez trouver, si x= a[n/ 2] alors x est trouvé et l'algorithme se termine ; si x

Pour plus d'articles connexes, veuillez visiter le Site Web PHP chinois ! !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!