Apprenez Python pour résoudre des problèmes mathématiques avancés

Python résout des problèmes de mathématiques avancés et ma mère n'a plus à se soucier de mes études

---

Utiliser Python pour résoudre les limites et dérivées en mathématiques avancées, dérivées partielles, intégrales définies, intégrales indéfinies, intégrales doubles et autres problèmes

Sympy est une bibliothèque de calcul scientifique Python, qui vise à devenir un système de calcul formel entièrement fonctionnel. SymPy comprend des fonctions allant de l'arithmétique symbolique de base au calcul, à l'algèbre, aux mathématiques discrètes et à la physique quantique. Il peut afficher les résultats dans LaTeX.

Site officiel de Sympy

Répertoire d'articles

• Python résout des problèmes de mathématiques avancés, et ma mère n'a plus à s'inquiéter mon étude
• 1. Compétences pratiques
• • 1.1 Fonction de signe
  • 1.2 Expansion de l'expression d'expansion
  • 1.3 Série de formules d'expansion de Taylor
  • 1.4 Expansion des signes
• 2. Trouver la limite
• 3. Trouver la dérivée diff
• • 3.1 Univarié. fonction
  • 3.2 Fonctions multivariées
• 4. Intégrale intégrale
• • 4.1 Intégrale définie
  • 4.2 Intégrale indéfinie
  • 4.3 Double intégrale
• 5. Résoudre le système d'équations résoudre
• 6. Calculer la somme

(Recommandation d'apprentissage gratuite : tutoriel vidéo python)

Regardez En regardant cette photo, avez-vous l'impression de ne pas pouvoir respirer ? Python est là pour vous aider à le résoudre.

from sympy import *import sympy

Entrez la commande « x= symboles(« x ») » pour définir un symbole

x = Symbol("x")y = Symbol("y")

1. Conseils pratiques

1.1 Fonction symbole

sympy fournit de nombreux symboles mathématiques, résumés comme suit

• Unité imaginaire

sympy.I

• Naturel logarithme

sympy.E

• Infini

sympy.oo

• Pi

 sympy.pi

• Trouver la nième racine

 sympy.root(8,3)

• Prendre le logarithme

sympy.log(1024,2)

• Trouver la factorielle

sympy.factorial(4)

• Fonctions trigonométriques

sympy.sin(sympy.pi)sympy.tan(sympy.pi/4)sympy.cos(sympy.pi/2)

1.2 Développer l'expression développer

f = (1+x)**3expand(f)

$x^3+3x^2+3x+1$

1.3 泰勒展开公式series

ln(1+x).series(x,0,4)

$x-\frac{x^2}{2}+\frac{x^3}{3}+O\left(x^4\right)$

sin(x).series(x,0,8)

$x-\frac{x^3}{6}+\frac{x^5}{120}-\frac{x^7}{5040}+O\left(x^8\right)$

cos(x).series(x,0,9)

$1-\frac{x^2}{2}+\frac{x^4}{24}-\frac{x^6}{720}+\frac{x^8}{40320}+O\left(x^9\right)$

(1/(1+x)).series(x,0,5)

$1-x+x^2-x^3+x^4+O\left(x^5\right)$

tan(x).series(x,0,4)

$x+\frac{x^3}{3}+O\left(x^4\right)$

(1/(1-x)).series(x,0,4)

$1+x+x^2+x^3+O\left(x^4\right)$

(1/(1+x)).series(x,0,4)

$1-x+x^2-x^3+O\left(x^4\right)$

1.4 符号展开

a = Symbol("a")b = Symbol("b")#simplify( )普通的化简simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1))#trigsimp( )三角化简trigsimp(sin(x)/cos(x))#powsimp( )指数化简powsimp(x**a*x**b)

$x^{a+b}$

2. 求极限limit

limit(sin(x)/x,x,0)

$1$

f2=(1+x)**(1/x)

f2

${\left(x+1\right)}^{\frac{1}{x}}$

重要极限

f1=sin(x)/x
f2=(1+x)**(1/x)f3=(1+1/x)**x
lim1=limit(f1,x,0)lim2=limit(f2,x,0)lim3=limit(f3,x,oo)print(lim1,lim2,lim3)

1 E E

dir可以表示极限的趋近方向

f4 = (1+exp(1/x))f4

$e^{\frac{1}{x}}+1$

lim4 = limit(f4,x,0,dir="-")lim4

$1$

lim5 = limit(f4,x,0,dir="+")lim5

$\infty$

3. 求导diff

diff(函数,自变量,求导次数)

3.1 一元函数

求导问题

diff(sin(2*x),x)

$2\cos \left(2x\right)$

diff(ln(x),x)

$\frac{1}{x}$

3.2 多元函数

求偏导问题

diff(sin(x*y),x,y)

$-xy\sin \left(xy\right)+\cos \left(xy\right)$

4. 积分integrate

4.1 定积分

• 函数的定积分: integrate(函数，(变量，下限，上限))
• 函数的不定积分: integrate(函数,变量)

f = x**2 + 1integrate(f,(x,-1.1))

$-1.54366666666667$

integrate(exp(x),(x,-oo,0))

$1$

4.2 不定积分

f = 1/(1+x*x)integrate(f,x)

$\mathrm{atan}\left(x\right)$

4.3 双重积分

f = (4/3)*x + 2*y
integrate(f,(x,0,1),(y,-3,4))

$11.6666666666667$

5. 求解方程组solve

#解方程组#定义变量f1=x+y-3f2=x-y+5solve([f1,f2],[x,y])

{x: -1, y: 4}

6. 计算求和式summation

计算求和式可以使用sympy.summation函数，其函数原型为sympy.summation(f, *symbols, **kwargs)

**

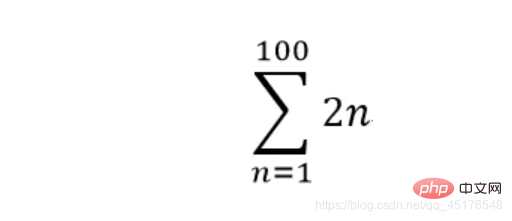
sympy.summation(2 * n,(n,1,100))

10100

到这里就结束了，如果对你有帮助，欢迎点赞关注评论，你的点赞对我很重要。在此也祝愿大家可以把数学学好

相关免费学习推荐：python教程（视频）

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!