Interview front-end : Implémentation de 6 algorithmes de tri classiques, combien en connaissez-vous ? (Animation ci-jointe + vidéo)

Cet article partagera avec vous les méthodes de mise en œuvre de 6 algorithmes de tri classiques. Il a une certaine valeur de référence. Les amis dans le besoin peuvent s'y référer. J'espère qu'il sera utile à tout le monde.

L'algorithme de tri est un point d'inspection à haute fréquence lors des entretiens, et nous devons le maîtriser. Cet article a compilé les algorithmes de tri les plus classiques et les plus couramment utilisés et les a associés à des animations et des vidéos, dans l'espoir de vous aider à les gagner plus facilement.

Tout d'abord, selon les caractéristiques de l'algorithme de tri, il peut être divisé en deux catégories suivantes :

• Tri comparatif
• Tri sans comparaison

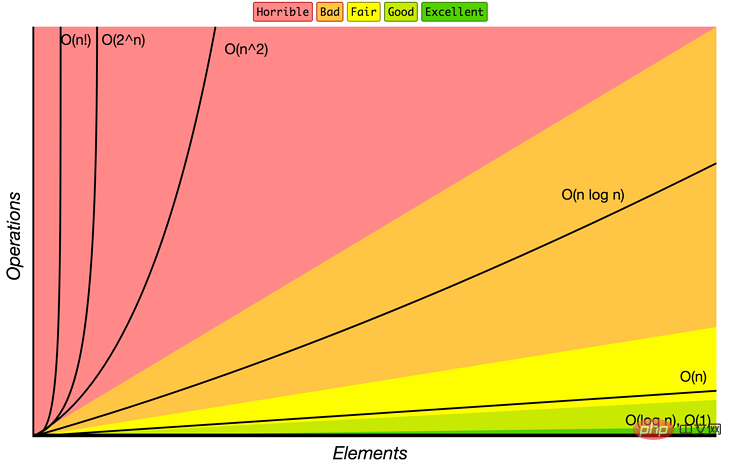
Comme son nom l'indique, la complexité temporelle du 比较类排序是通过元素间的比较进行排序的，非比较类则不涉及元素之间的比较操作。

tri par comparaison ne peut pas dépasser O(nlogn), également connu sous le nom de 非线性排序。

La complexité temporelle du tri non comparatif peut dépasser O(nlogn) et peut s'exécuter en temps linéaire. Elle est également appelée 线性排序。

<.> si vous ne comprenez pas encore le temps. Pour la complexité, vous pouvez vous référer à ma chronique sur l'analyse de la complexité temporelle et spatiale de l'algorithme JavaScript.

01 Tri à bulles

Vidéo de visualisation du tri à bulles :

https://www.reddit.com/r /programming/comments /e55j0i/bubble_sort_visualization/

Tri des bulles, simple et grossier, explication en une phrase :

Le tri des bulles est en

pour voir s'il répond aux exigences de relation de taille Si vous. vous n'êtes pas satisfait, échangez-les. Répétez jusqu'à ce que plus aucun échange ne soit nécessaire, c'est-à-dire que le tri soit terminé. 每次冒泡操作时会比较相邻的两个元素

const bubbleSort = function(arr) {
  const len = arr.length
  if (len < 2) return arr
  for (let i = 0; i < len; i++) {
      for (let j = 0; j < len - i - 1; j++) {
          if (arr[j] > arr[j + 1]) {
              const temp = arr[j]
              arr[j] = arr[j + 1]
              arr[j + 1] = temp
          }
      }
  }
  return arr
}

Complexité temporelle : O(n^2)
Complexité spatiale : O(1)
Stable

注意：这里的稳定是指，冒泡排序是稳定的排序算法。

Qu'est-ce qu'un algorithme de tri stable ?

Stabilité de l'algorithme de tri

Il ne suffit pas d'utiliser simplement

et 执行效率 pour juger de la qualité de l'algorithme de tri. , il existe une autre métrique importante, 内存消耗. 稳定性

signifie,

如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。

Par exemple :

Par exemple, nous avons un ensemble de données : 1, 9, 2, 5, 8, 9. Après tri par taille, il s'agit de 1, 2, 5, 8, 9, 9.

Il y a deux 9 dans cet ensemble de données. Après tri par un certain algorithme de tri, si l'ordre des deux 9 ne change pas, nous appelons cet algorithme de tri

. 稳定的排序算法Sinon, c'est
. 不稳定的排序算法

Optimisation du tri des bulles

Le code ci-dessus peut également être optimisé Lorsqu'une certaine opération de bulle a été

, cela signifie qu'elle a été complètement ordonnée, et. pas besoin Ensuite, continuez à effectuer les opérations de bullage ultérieures. 没有数据交换时

const bubbleSort = function(arr) {
  const len = arr.length
  let flag = false
  if (len < 2) return arr
  for (let i = 0; i < len; i++) {
      flag = false // 提前退出冒泡循环的标志
      for (let j = 0; j < len - i - 1; j++) {
          if (arr[j] > arr[j + 1]) {
              const temp = arr[j]
              arr[j] = arr[j + 1]
              arr[j + 1] = temp
              flag = true // 表示有数据交换
          }
      }
      if (!flag) break // 没有数据交换，提前退出
  }
  return arr
}

02 Tri par insertion

Tri par insertion, comme son nom l'indique, pour les données non triées, dans Parcourez la séquence triée d'arrière en avant, trouvez la position correspondante et insérez-la, en gardant les éléments de la séquence triée dans l'ordre.

Commencez à parcourir à partir de i égal à 1, obtenez le courant de l'élément actuel et comparez-le avec l'élément précédent.

Si l'élément précédent est supérieur à l'élément actuel, échangez l'élément précédent avec l'élément actuel et continuez la boucle jusqu'à ce que l'élément de la séquence non triée soit vide et que le tri soit terminé.

const insertSort = function(arr) {
    const len = arr.length
    let curr, prev
    for (let i = 1; i < len; i++) {
        curr = arr[i]
        prev = i - 1
        while (prev >= 0 && arr[prev] > curr) {
            arr[prev + 1] = arr[prev]
            prev--
        }
        arr[prev + 1] = curr
    }
    return arr
}

Complexité temporelle : O(n^2)
Complexité spatiale : O(1)
Stable

03 Tri par sélection

Vidéo de visualisation du tri par sélection :

https://www.reddit.com/r/programming/comments/e5md13/selection_sort_visualization /

Le tri par sélection est quelque peu similaire au tri par insertion et est également divisé en séquences triées et séquences non triées.

Mais le tri de sélection est

. Et ainsi de suite jusqu'à ce que le tri soit terminé. 将最小的元素存放在数组起始位置，再从剩下的未排序的序列中寻找最小的元素，然后将其放到已排序的序列后面

const selectSort = function(arr) {
    const len = arr.length
    let temp, minIndex
    for (let i = 0; i < len - 1; i++) {
        minIndex = i
        for (let j = i + 1; j < len; j++) {
            if (arr[j] <= arr[minIndex]) {
                minIndex = j
            }
        }
        temp = arr[i]
        arr[i] = arr[minIndex]
        arr[minIndex] = temp
    }
    return arr
}

Complexité temporelle : O(n^2)
Complexité spatiale : O(1)
Instable

04 Tri par fusion

Une application typique de l'algorithme diviser pour régner L'idée de diviser pour régner. L'algorithme de conquête est largement basé sur la récursivité et est plus approprié pour être implémenté en utilisant la récursivité.

处理过程是由下到上的，先处理子问题，然后再合并。

如果感觉自己对递归掌握的还不是很透彻的同学，可以移步我的这篇专栏你真的懂递归吗？。

顾名思义，分而治之。一般分为以下三个过程：

• 分解：将原问题分解成一系列子问题。

• 解决：递归求解各个子问题，若子问题足够小，则直接求解。

• 合并：将子问题的结果合并成原问题。

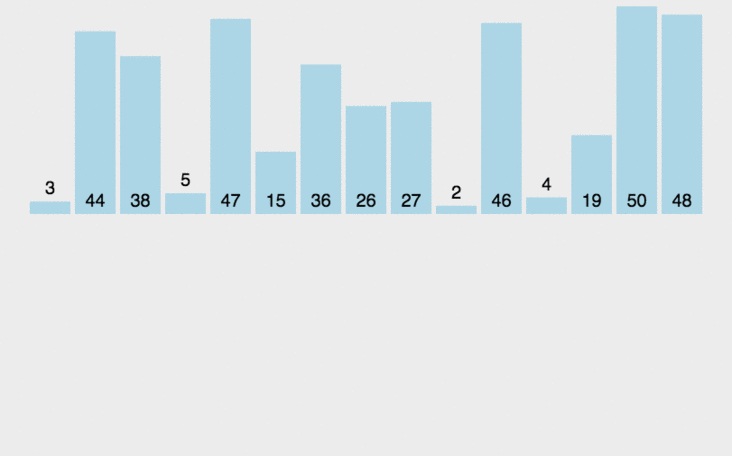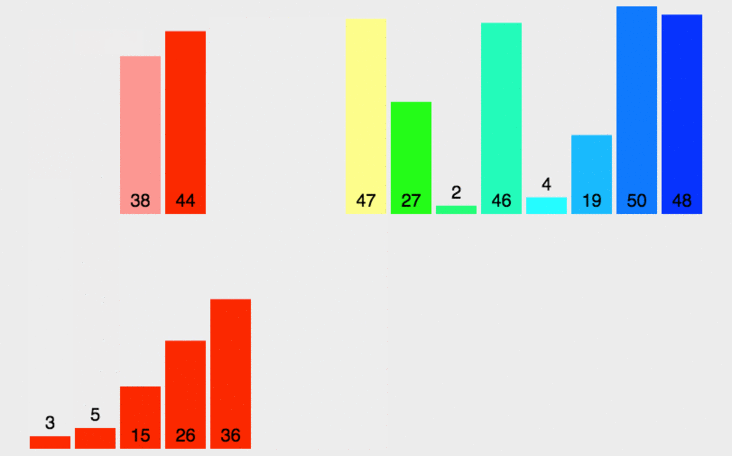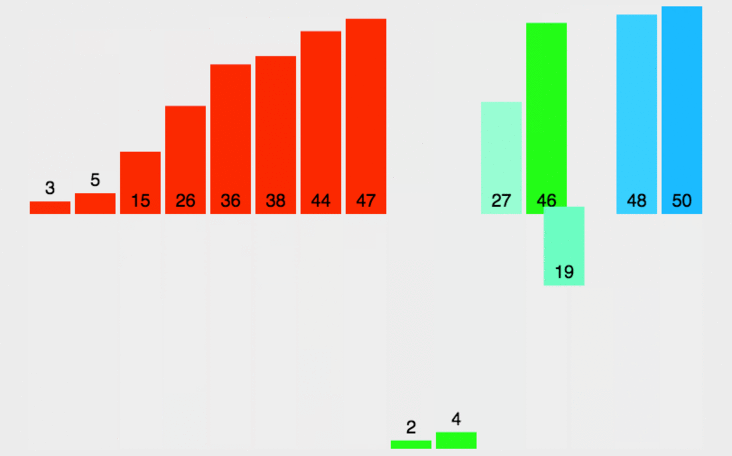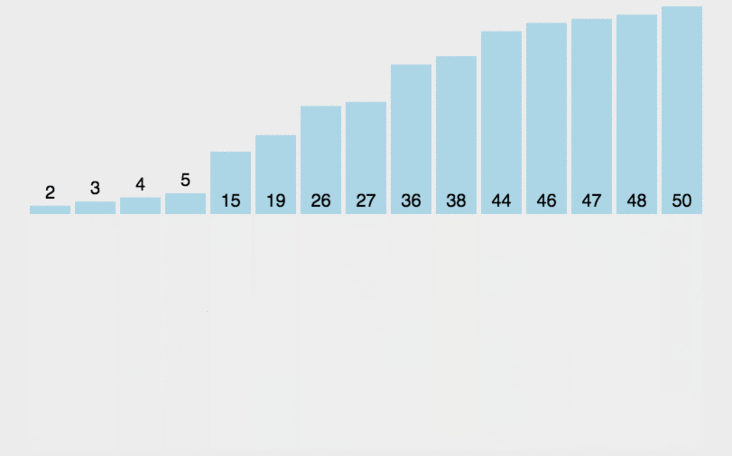
归并排序就是将待排序数组不断二分为规模更小的子问题处理，再将处理好的子问题合并起来，这样整个数组就都有序了。

const mergeSort = function(arr) {
    const merge = (right, left) => {
    const result = []
    let i = 0, j = 0
    while (i < left.length && j < right.length) {
      if (left[i] < right[j]) {
        result.push(left[i++])
      } else {
        result.push(right[j++])
      }
    }
    while (i < left.length) {
      result.push(left[i++])
    }
    while (j < right.length) {
      result.push(right[j++])
    }
    return result
    }
    const sort = (arr) => {
        if (arr.length === 1) { return arr }
        const mid = Math.floor(arr.length / 2)
        const left = arr.slice(0, mid)
        const right = arr.slice(mid, arr.length)
        return merge(mergeSort(left), mergeSort(right))
    }
    return sort(arr)
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(n)
• 稳定

05 快速排序 Quick Sort

快速排序可视化视频：

https://www.reddit.com/r/dataisbeautiful/comments/e9fb2k/oc_quicksort_visualization/

快速排序也是分治法的应用，处理过程是由上到下的，先分区，然后再处理子问题。

快速排序通过遍历数组，将待排序元素分隔成独立的两部分，一部分记录的元素均比另一部分的元素小，则可以分别对这两部分记录的元素继续进行排序，直到排序完成。

这就需要从数组中挑选出一个元素作为 基准(pivot)，然后重新排序数列，将元素比基准值小的放到基准前面，比基准值大的放到基准后面。

然后将小于基准值的子数组(left)和大于基准值的子数组(right)递归地调用 quick 方法，直到排序完成。

const quickSort = function(arr) {
    const quick = function(arr) {
        if (arr.length <= 1) return arr
        const len = arr.length
        const index = Math.floor(len >> 1)
        const pivot = arr.splice(index, 1)[0]
        const left = []
        const right = []
        for (let i = 0; i < len; i++) {
            if (arr[i] > pivot) {
                right.push(arr[i])
            } else if (arr[i] <= pivot) {
                left.push(arr[i])
            }
        }
        return quick(left).concat([pivot], quick(right))
    }
    const result = quick(arr)
    return result
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(nlogn)
• 不稳定

06 堆排序 Heap Sort

堆排序相比其他几种排序代码会有些复杂，不过没关系，我们先来看一些前置知识，可以帮助我们更好的理解堆排序。

堆排序顾名思义就是要利用堆这种数据结构进行排序。堆是一种特殊的树，满足以下两点就是堆：

• 堆是一个完全二叉树

• 堆中每一个节点的值都必须大于等于(或小于等于)其子树中的每个节点的值

每个节点的值都大于等于子树中每个节点值的堆，叫做大顶堆，每个节点的值都小于等于子树中每个节点值的堆，叫做小顶堆。

也就是说，大顶堆中，根节点是堆中最大的元素。小顶堆中，根节点是堆中最小的元素。

如果你对树这种数据结构还不是很了解，可以移步我的这篇专栏“树”业有专攻

堆如果用一个数组表示的话，给定一个节点的下标 i (i从1开始)，那么它的父节点一定为 A[i / 2]，左子节点为 A[2i]，右子节点为 A[2i + 1]。

堆排序包含两个过程，建堆和排序。首先构建一个大顶堆，也就是将最大值存储在根节点(i = 1)，每次取大顶堆的根节点与堆的最后一个节点进行交换，此时最大值放入了有效序列的最后一位，并且有效序列减 1，有效堆依然保持完全二叉树的结构，然后进行堆化成为新的大顶堆。重复此操作，直到有效堆的长度为 0，排序完成。

const heapSort = function(arr) {
    buildHeap(arr, arr.length - 1)
    let heapSize = arr.length - 1 // 初始化堆的有效序列长度
    for (let i = arr.length - 1; i > 1; i--) {
        swap(arr, 1, i) // 交换堆顶元素与最后一个有效子元素
        heapSize-- // 有效序列长度减 1
        heapify(arr, heapSize, 1) // 堆化有效序列
    }
    return arr
}

// 构建大顶堆
const buildHeap = function(items, heapSize) {
    // 从后往前并不是从序列的最后一个元素开始，而是从最后一个非叶子节点开始，这是因为，叶子节点没有子节点，不需要自上而下式堆化。
    // 最后一个子节点的父节点为 n/2 ，所以从 n/2 位置节点开始堆化
    for (let i = Math.floor(heapSize / 2); i >= 1; i--) {
        heapify(items, heapSize, i)
    }
}
// 堆化
const heapify = function(arr, heapSize, i) {
    while (true) {
        let maxIndex = i
        if (2 * i <= heapSize && arr[i] < arr[i * 2]) {
            maxIndex = i * 2
        }
        if (2 * i + 1 <= heapSize && arr[maxIndex] < arr[i * 2 + 1]) {
            maxIndex = i * 2 + 1
        }
        if (maxIndex === i) break
        swap(arr, i, maxIndex)
        i = maxIndex
    }
}

// 交换工具函数
const swap = function(arr, i, j) {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

• 时间复杂度: O(nlogn)
• 空间复杂度: O(1)
• 不稳定

为了方便你理解和记忆，我将这 6 种排序算法的复杂度和稳定性汇总成表格如下：

本文讲解了十大经典排序算法中的 6 种排序算法，这 6 种排序算法是平时开发中比较常见的，大家务必要熟练掌握。

更多编程相关知识，请访问：编程视频！！

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!