Quelle est la complexité temporelle du tri à bulles, du tri rapide et du tri par tas ?

La complexité temporelle du tri à bulles : le meilleur des cas est "O(n)", le pire des cas est "O(n2)". La complexité temporelle du tri rapide : le meilleur des cas est "O(nlogn)", le pire des cas est "O(n2)". La complexité temporelle du tri par tas est "O(nlogn)".

L'environnement d'exploitation de ce tutoriel : système Windows 7, ordinateur Dell G3.

Tri à bulles

Complexité temporelle

Meilleur des cas : le tableau lui-même est séquentiel, le parcours de la boucle externe est terminé une fois O(n)

Dans le pire des cas : le tableau lui-même est dans l'ordre inverse et la boucle interne et externe traverse la O(n2)

complexité spatiale
Créer un espace séquence d'échange O(1)
Stabilité
稳定, car si le jugement n'est pas vrai, la commande ne sera pas échangée, et les mêmes éléments ne seront pas échangés

• Le tri à bulles est le plus simple de tous les algorithmes de tri. Cependant, du point de vue du temps d'exécution, le tri à bulles est le pire, sa complexité est O(n2) .

• Le tri à bulles compare deux éléments adjacents et les échange si le premier est supérieur au second. Les éléments sont déplacés dans le bon ordre comme si des bulles remontaient à la surface, d'où le nom de tri à bulles.

• Lors de l'échange, nous utilisons une valeur intermédiaire pour stocker la valeur d'un certain article d'échange. D'autres méthodes de tri utiliseront également cette méthode, nous déclarons donc une méthode pour placer ce code d'échange en vue de sa réutilisation. En utilisant ES6 (ECMAScript 2015) ** propriétés d'objet améliorées - syntaxe d'affectation de déstructuration pour les tableaux d'objets, ** cette fonction peut être écrite comme suit :

[array[index1], array[index2]] = [array[index2], array[index1]];

Implémentation spécifique :

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {//外循环（行{2}）会从数组的第一位迭代 至最后一位，它控制了在数组中经过多少轮排序
    for (let j = 0; j < arr.length - i; j++) {//内循环将从第一位迭代至length - i位，因为后i位已经是排好序的，不用重新迭代
      if (arr[j] > arr[j + 1]) {//如果前一位大于后一位
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];//交换位置
      }
    }
  }
  return arr;
}

Tri rapide

Complexité temporelle
Meilleur des cas : chaque fois que la valeur de base divise simplement l'ensemble du tableau de manière égale, O(nlogn)
Pire des cas : à chaque fois Chaque valeur de base est la valeur maximale/minimale dans le tableau, O(n2)

Complexité spatiale
Le tri rapide est récursif et nécessite l'utilisation d'une pile pour enregistrer chaque niveau d'informations d'appel de récursion, donc la complexité spatiale est cohérente avec la profondeur de l'arbre récursif
Meilleur des cas : chaque valeur de base divise l'ensemble du tableau de manière égale, et la profondeur de l'arbre récursif O(logn)
Pire des cas : chaque valeur de base Ils sont tous les valeurs maximales/minimales dans le tableau, la profondeur de l'arbre de récursion O(n)

stabilité
le tri rapide est 不稳定 car les mêmes mots-clés peuvent être échangés .
Le tri rapide est récursif,
Cas particulier : gauche>droite, sortie directe.

Étapes :

(1) Tout d'abord, sélectionnez l'élément du milieu du tableau comme pivotbase, prenez généralement le premier une valeur .

(2) Créez deux pointeurs, celui de gauche pointe vers le premier élément du tableau et celui de droite pointe vers le dernier élément du tableau. Déplacez le pointeur droit jusqu'à trouver un élément plus petit que le pivot, puis déplacez le pointeur gauche jusqu'à trouver un élément plus grand que le pivot, puis échangez-les, répétez ce processus jusqu'à ce que le pointeur gauche rencontre le pointeur droit. Ce processus entraînera le tri des valeurs inférieures au pivot avant le pivot et le tri des valeurs supérieures au pivot après le pivot. Cette étape est appelée opération de partition.

(3) Puis échangez l'élément pivot et l'élément à la position où le pointeur s'arrête (ce qui équivaut à ramener cet élément à sa position d'origine . Le celui à gauche de cet élément est plus petit que l'élément

Petit, celui de droite est plus grand que lui, cette position est sa position finale)

(4) Ensuite, l'algorithme divise le petit tableau (un sous-tableau composé de valeurs plus petites que l'élément pivot et un sous-tableau composé de valeurs plus petites que l'élément pivot) sous-tableau composé de valeurs plus grandes les unes que les autres) répétez les deux étapes précédentes ( méthode récursive

), la sortie du

left/right=i récursif est

, c'est-à-dire :

left>i-1 / i+1>right

À ce stade, le tableau de sous-tableaux a été trié.

Schéma de référencement :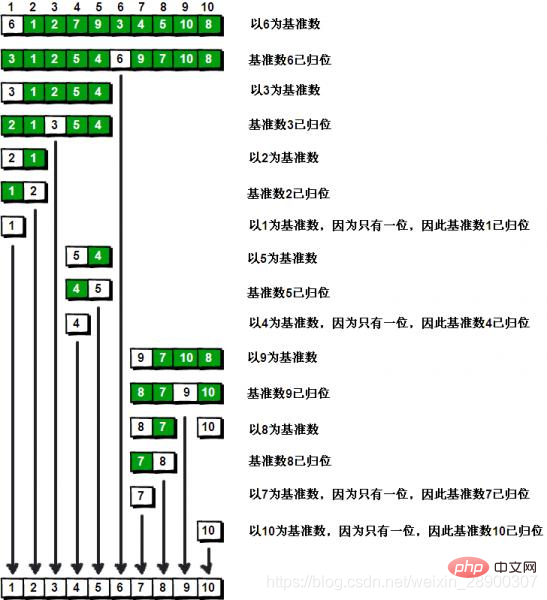

Implémentation spécifique :

function quicksort(arr, left, right) {
  if (left > right) {
    return;
  }
  var i = left,
    j = right,
    base = arr[left]; //基准总是取序列开头的元素
  //   var [base, i, j] = [arr[left], left, right]; //以left指针元素为base
  while (i != j) {
    //i=j，两个指针相遇时，一次排序完成，跳出循环
    // 因为每次大循环里面的操作都会改变i和j的值，所以每次循环/操作前都要判断是否满足i<j
    while (i < j && arr[j] >= base) {
      //寻找小于base的右指针元素a，跳出循环，否则左移一位
      j--;
    }
    while (i < j && arr[i] <= base) {
      //寻找大于base的左指针元素b，跳出循环，否则右移一位
      i++;
    }
    if (i < j) {
      [arr[i], arr[j]] = [arr[j], arr[i]]; //交换a和b
    }
  }
  [arr[left], arr[j]] = [arr[j], arr[left]]; //交换相遇位置元素和base，base归位
  //   let k = i;
  quicksort(arr, left, i - 1); //对base左边的元素递归排序
  quicksort(arr, i + 1, right); //对base右边的元素递归排序
  return arr;
}

Référence : https://www.cnblogs.com/venoral/p/5180439 html.

Tri par tas

Concept de tas<🎜>

• 堆是一个完全二叉树。
• 完全二叉树： 二叉树除开最后一层，其他层结点数都达到最大，最后一层的所有结点都集中在左边（左边结点排列满的情况下，右边才能缺失结点）。
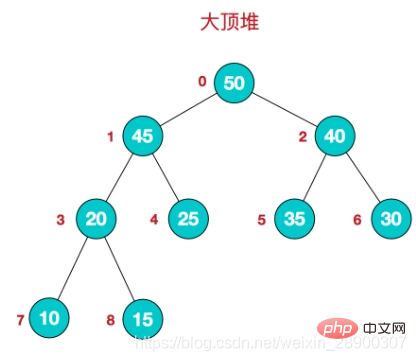
• 大顶堆：根结点为最大值，每个结点的值大于或等于其孩子结点的值。
• 小顶堆：根结点为最小值，每个结点的值小于或等于其孩子结点的值。
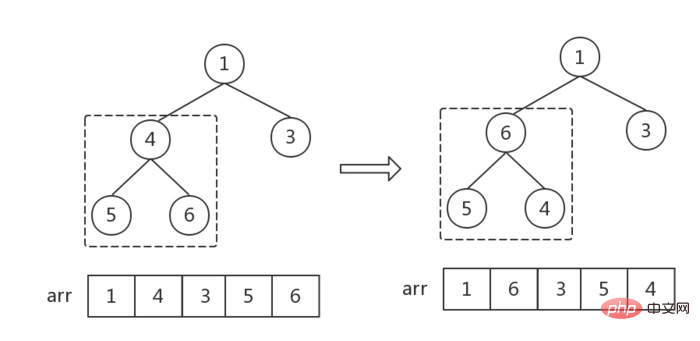
• 堆的存储： 堆由数组来实现，相当于对二叉树做层序遍历。如下图：
  
  

时间复杂度
总时间为建堆时间+n次调整堆 —— O(n)+O(nlogn)=O(nlogn)
建堆时间：从最后一个非叶子节点遍历到根节点，复杂度为O(n)
n次调整堆：每一次调整堆最长的路径是从树的根节点到叶子结点，也就是树的高度logn，所以每一次调整时间复杂度是O(logn)，一共是O(nlogn)

空间复杂度
堆排序只需要在交换元素的时候申请一个空间暂存元素，其他操作都是在原数组操作，空间复杂度为O(1)

稳定性
堆排序是不稳定的，因为可能会交换相同的子结点。

步骤一：建堆

• 以升序遍历为例子，需要先将将初始二叉树转换成大顶堆，要求满足：树中任一非叶子结点大于其左右孩子。
• 实质上是调整数组元素的位置，不断比较，做交换操作。
• 找到第一个非叶子结点——Math.floor(arr.length / 2 - 1)，从后往前依次遍历
• 对每一个结点，检查结点和子结点的大小关系，调整成大根堆

// 建立大顶堆
function buildHeap(arr) {
  //从最后一个非叶子节点开始，向前遍历，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则
  }
}

步骤二：调整指定结点形成大根堆

• 建立childMax指针指向child最大值节点，初始值为2 * cur + 1，指向左节点
• 当左节点存在时（左节点索引小于数组length），进入循环，递归调整所有节点位置，直到没有左节点为止（cur指向一个叶结点为止），跳出循环，遍历结束
• 每次循环，先判断右节点存在时，右节点是否大于左节点，是则改变childMax的指向
• 然后判断cur根节点是否大于childMax，
• 大于的话，说明满足大顶堆规律，不需要再调整，跳出循环，结束遍历
• 小于的话，说明不满足大顶堆规律，交换根节点和子结点，
• 因为交换了节点位置，子结点可能会不满足大顶堆顺序，所以还要判断子结点然后，改变cur和childMax指向子结点，继续循环判断。

//从输入节点处调整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引

  //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构
  while (childMax < len) {
    //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子树值小于根节点，不需要调整，退出循环
    if (arr[childMax] < arr[cur]) break;
    //子树值大于根节点，需要调整，先交换根节点和子节点
    swap(arr, childMax, cur);
    cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则
    childMax = 2 * cur + 1; //子节点指针指向新的子节点
  }
}

步骤三：利用堆进行排序

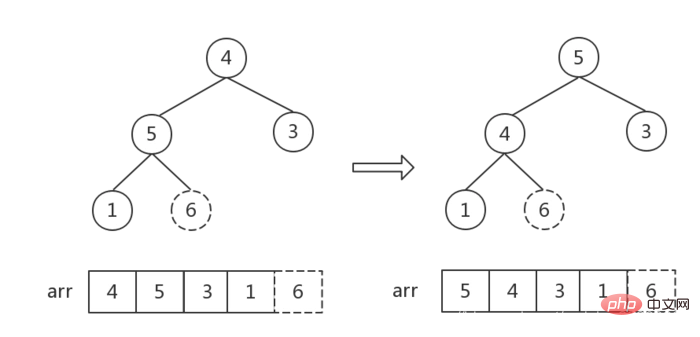
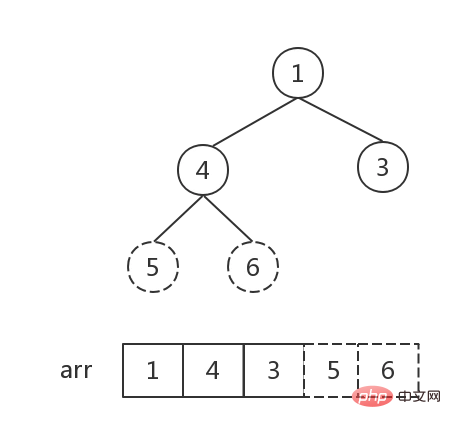
• 从后往前遍历大顶堆（数组），交换堆顶元素a[0]和当前元素a[i]的位置，将最大值依次放入数组末尾。
• 每交换一次，就要重新调整一下堆，从根节点开始，调整根节点～i-1个节点（数组长度为i），重新生成大顶堆
  
  

// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //构建大顶堆
  buildHeap(arr);
  //从后往前遍历，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置
    headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆
  }
  return arr;
}

完整代码：

// 交换数组元素
function swap(a, i, j) {
  [a[i], a[j]] = [a[j], a[i]];
}
//从输入节点处调整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子树中较大的位置，初始值为左子树的索引

  //子树存在（索引没超过数组长度）而且子树值大于根时，此时不符合大顶堆结构，进入循环，调整堆的结构
  while (childMax < len) {
    //判断左右子树大小,如果右子树更大，而且右子树存在，childMax指针指向右子树
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子树值小于根节点，不需要调整，退出循环
    if (arr[childMax] < arr[cur]) break;
    //子树值大于根节点，需要调整，先交换根节点和子节点
    swap(arr, childMax, cur);
    cur = childMax; //根节点指针指向子节点，检查子节点是否满足大顶堆规则
    childMax = 2 * cur + 1; //子节点指针指向新的子节点
  }
}
// 建立大顶堆
function buildHeap(arr) {
  //从最后一个非叶子节点开始，向前遍历，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //对每一个节点都调整堆，使其满足大顶堆规则
  }
}
// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //构建大顶堆
  buildHeap(arr);
  //从后往前遍历，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交换最后位置和第一个位置（堆顶最大值）的位置
    headAdjust(arr, 0, i); //调整根节点～i-1个节点，重新生成大顶堆
  }
  return arr;
}

更多编程相关知识，请访问：编程视频！！

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!