Comment implémenter la factorielle de n en php

Comment implémenter la factorielle de n en PHP : 1. Par récursion ordinaire, le code est comme "function fact(int $n): int{...}" 2. Par la boucle ordinaire, le code ressemble à " while ($num

L'environnement d'exploitation de cet article : système Windows 10, PHP version 7.2.15, ordinateur DELL G3

Comment fonctionne php réaliser la factorielle de n ?

Autant que je sache, les méthodes d'implémentation de la factorielle peuvent généralement être divisées en trois types. La récursivité et le bouclage au sens habituel sont chacun considérés comme un seul, et il y en a aussi. une grande catégorie qui utilise des méthodes mathématiques intelligentes pour réduire le nombre d'opérations (en particulier le nombre d'opérations de multiplication), optimisant ainsi l'efficacité du calcul.

Si vous souhaitez considérer la factorielle de grands entiers de haute précision, la situation sera plus compliquée pour le langage PHP. Par exemple, lors de l'utilisation de certaines méthodes fournies par l'extension BCMath, la conversion explicite de nombres et de chaînes. Les opérations sont fréquemment comparées.

Cet article considère n comme un entier et tente d'implémenter respectivement les situations ci-dessus. Des exemples de code disponibles sont donnés dans chaque cas, et une comparaison complète de plusieurs méthodes est jointe à la fin de l'article.

Implémentation récursive ordinaire

La première est l'implémentation récursive ordinaire Selon la formule récursive générale fact(n) = n * fact(n-1), elle. est facile d’écrire le code de calcul factoriel. L'avantage de l'implémentation récursive ordinaire est que le code est relativement concis et que le même processus que la formule générale rend le code facile à comprendre. L'inconvénient est que, comme il doit s'appeler fréquemment, un grand nombre d'opérations push et pop sont nécessaires et l'efficacité globale du calcul n'est pas élevée (voir le tableau à la fin de l'article).

function fact(int $n): int
{
    if ($n == 0) {
        return 1;
    }
    return $n * fact($n - 1);
}

Implémentation de boucle ordinaire

L'implémentation de boucle ordinaire a un peu de saveur de "programmation dynamique", mais en raison de la faible fréquence d'utilisation des variables d'état intermédiaires, aucun supplément un espace de stockage est requis, c'est donc plus simple que l'algorithme de programmation dynamique général. La méthode récursive ordinaire est un processus de calcul descendant (de n à 1), tandis que la boucle ordinaire est un calcul ascendant.

Donc, relativement parlant, le code n'est pas aussi intuitif que la méthode ci-dessus, mais comme les processus push et pop sont moins fréquents, l'efficacité du calcul sera plus élevée (voir le tableau à la fin de l'article).

function fact(int $n): int
{
    $result = 1;
    $num = 1;
    while ($num <= $n) {
        $result = $result * $num;
        $num = $num + 1;
    }
    return $result;
}

Factielle de grands entiers auto-implémentée

En raison de la limitation de plage du type int en PHP, les deux méthodes ci-dessus ne peuvent calculer avec précision que des factorielles jusqu'à 20. Si vous ne considérez que la factorielle de 20, il sera plus rapide d'utiliser la méthode de la table de recherche : calculez la factorielle de 0 à 20 à l'avance et stockez-la dans un tableau, et interrogez-la une fois si nécessaire.

Afin de pouvoir s'adapter à la factorielle des grands nombres et obtenir des résultats de calcul précis, cet article est amélioré sur la base de la "méthode de la boucle ordinaire", en utilisant un tableau pour stocker chaque bit du résultat du calcul ( de bas en haut), et en multipliant la méthode de retenue calcule le résultat de chaque bit tour à tour.

Il va sans dire que l'avantage de cette méthode est qu'elle peut être appliquée à des situations factorielles de grands nombres de haute précision. L'inconvénient est que pour les factorielles décimales, le processus de calcul est complexe et lent.

function fact(int $n): array
{
    $result = [1];
    $num = 1;
    while ($num <= $n) {
        $carry = 0;
        for ($index = 0; $index < count($result); $index++) {
            $tmp = $result[$index] * $num + $carry;
            $result[$index] = $tmp % 10;
            $carry = floor($tmp / 10);
        }
        while ($carry > 0) {
            $result[] = $carry % 10;
            $carry = floor($carry / 10);
        }
        $num = $num + 1;
    }
    return $result;
}

Méthode d'extension BCMath

BCMath est une extension mathématique pour PHP qui gère les calculs numériques sur des nombres (de toute taille et précision) représentés par des chaînes. Puisqu'il s'agit d'une extension implémentée en langage C, la vitesse de calcul sera plus rapide que l'auto-implémentation ci-dessus.

Apprentissage recommandé : "Tutoriel vidéo PHP"

Sur mon ordinateur portable, je calcule également la factorielle de 2000. Il faut en moyenne 0,5 à 0,6 seconde pour la mettre en œuvre par moi-même. Utiliser BCMath prend 0,18 à 0,19 seconde. Le principal inconvénient de cette méthode est qu'elle nécessite l'installation des extensions correspondantes, ce qui ne constitue pas un changement au niveau du code. Pour les applications où les mises à niveau de la gestion environnementale ne sont pas pratiques, l'aspect pratique est discutable.

function fact(int $n): string
{
    $result = '1';
    $num = '1';
    while ($num <= $n) {
        $result = bcmul($result, $num);
        $num = bcadd($num, &#39;1&#39;);
    }
    return $result;
}

Algorithme d'optimisation

Comme mentionné au début de cet article, l'algorithme d'optimisation tente de réduire autant le nombre d'opérations (notamment le nombre d'opérations de multiplication) que possible pour obtenir une factorielle rapide. Considérant que pour les factorielles de petits entiers, l'algorithme le plus rapide devrait être la méthode de recherche de table, avec une complexité temporelle de O(1), donc cette section discute et teste principalement la factorielle exacte des grands entiers.

Il est entendu que l'optimisation factorielle est actuellement plus courante via n = C(n, n/2) * (n/2) * (n/2) ! La formule réside principalement dans l’optimisation de C(n, n/2). Considérant que dans le cas de grands entiers, l'efficacité du langage PHP pour implémenter C(n, n/2) n'est pas élevée et que la lisibilité du code est relativement mauvaise (conversion explicite fréquente de nombres et de chaînes), cet article utilise donc Une autre méthode plus intelligente.

La vitesse de calcul de la multiplication est généralement inférieure à celle de l'addition et de la soustraction. En réduisant le nombre d'opérations de multiplication, la vitesse globale de calcul peut être améliorée. Par induction mathématique, on peut constater que pour la factorielle de n, on peut trouver successivement des valeurs qui sont 1, 1+3, 1+3+5... inférieures à (n/2)^2, puis multiplier les en séquence pour obtenir la valeur cible.

L'avantage de cet algorithme est que la vitesse de calcul est rapide, mais l'inconvénient est que le processus de mise en œuvre n'est pas intuitif et facile à comprendre. Après le test, le code suivant calcule le temps moyen factoriel de 2 000 à 0,11 seconde, soit environ la moitié du temps de la méthode de boucle ordinaire.

En plus de cette méthode d'optimisation, nous avons également vu d'autres idées similaires, comme vérifier à plusieurs reprises si les nombres dans 1...n sont divisibles par 2, enregistrer le nombre de fois divisible par 2 x, et essayer de généraliser Trouvez la formule commune de multiplication des nombres impairs, et enfin multipliez-la par 2^x pour obtenir le résultat.

function fact(int $n): string
{
    $middleSquare = pow(floor($n / 2), 2);
    $result = $n & 1 == 1 ? 2 * $middleSquare * $n : 2 * $middleSquare;
    $result = (string)$result;
    for ($num = 1; $num < $n - 2; $num = $num + 2) {
        $middleSquare = $middleSquare - $num;
        $result = bcmul($result, (string)$middleSquare);
    }
    return $result;
}

综合对比

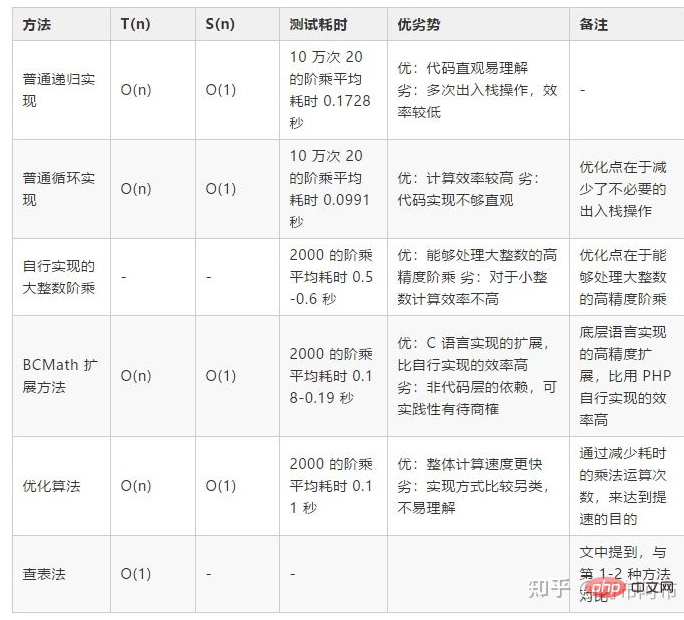
本文中提到的方法是按照由劣到优的顺序，因此，下列表格中每一行中提到优劣势，主要是和其上一两种方法对比。

表格中「测试耗时」一列的测试环境为个人笔记本，硬件配置为 Dell/i5-8250U/16GB RAM/256GB SSD Disk，软件配置为 Win 10/PHP 7.2.15。

总结

虽然本文将实现方法分为三大类，但其实也可以分为循环和递归两大类，在这两类中分别使用相应的算法优化计算效率。But，总体而言，循环的效率要优于递归。

讲道理，本文中使用的优化算法并不是最优解，只是用 PHP 相对好实现，代码易读性也比较高。有兴趣的读者可以谷歌了解更多的骚操作。

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!