Comment le parcours dans l'ordre est-il effectué ?

La méthode de parcours du parcours dans l'ordre est la suivante : pour le nœud actuel, parcourez d'abord le sous-arbre de gauche, puis visitez le nœud actuel et enfin parcourez le sous-arbre de droite. Le parcours dans l'ordre est un type de parcours d'arbre binaire, également appelé parcours à mi-racine et tour dans l'ordre.

L'environnement d'exploitation de ce tutoriel : système Windows 7, version C++17, ordinateur Dell G3.

L'arbre binaire est une structure de données importante, et il est également important de parcourir l'arbre binaire. Nous présentons ici brièvement trois méthodes de parcours dans l’ordre des arbres binaires. La traversée dans l'ordre d'un arbre binaire traverse d'abord le sous-arbre de gauche, puis visite le nœud actuel et traverse enfin le sous-arbre de droite. Pour l'arbre binaire suivant, le résultat du parcours dans l'ordre est le suivant :

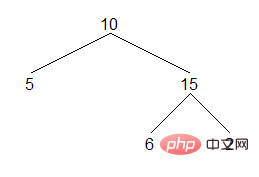
Le résultat : [5,10,6,15,2]

Intuitivement, le parcours dans l'ordre d'un arbre binaire consiste à projeter les nœuds sur une coordonnée horizontale. Comme le montre l'image :

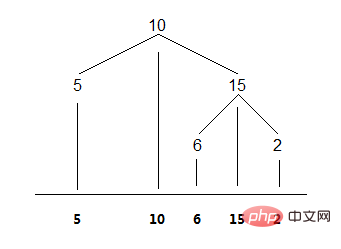
1. Méthode récursive

C'est la méthode la plus simple, facile à penser et facile à mettre en œuvre. La condition de fin de la récursion est de savoir si le nœud actuel est vide. L'appel récursif traverse d'abord le sous-arbre de gauche, puis visite le nœud actuel et enfin le sous-arbre de droite est appelé de manière récursive. Le code est le suivant :

//recursive
class Solution1 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        inorderHelper(ret,root);
        return ret;
    }
private:
    void inorderHelper(vector<int>& ret,TreeNode* root)
    {
        if(root==NULL)return;
        inorderHelper(ret,root->left);
        ret.push_back(root->val);
        inorderHelper(ret,root->right);
    }
};

2. Méthode itérative

Dans la méthode itérative, partez du nœud racine pour trouver le nœud le plus à gauche de l'arbre binaire, enregistrez les nœuds passés dans une pile. , et trouvez le nœud le plus à gauche Après avoir visité le nœud, pour chaque nœud, c'est le nœud racine du sous-arbre avec lui-même comme racine. Après la visite, vous pouvez accéder au bon enfant. Le code est le suivant :

//iterate,using a stack
class Solution2 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        stack<TreeNode*> st;
        while(!st.empty()||curr!=NULL)
        {
            while(curr!=NULL)
            {
                st.push(curr);
                curr=curr->left;
            }
            curr=st.top();
            st.pop();
            ret.push_back(curr->val);
            curr=curr->right;
        }
        return ret;
    }
};

La complexité temporelle de cette méthode est O(n), et la complexité spatiale est également O(n).

3. Méthode Morris

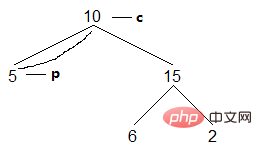
Cette méthode a été inventée par Morris Après l'avoir lue, je la trouve extrêmement exquise. Cette méthode n'utilise pas de récursivité, n'utilise pas la pile et complète la traversée de l'arbre binaire avec une complexité spatiale O(1). L'idée de base de cette méthode est de pointer le fils droit de tous les nœuds dont le fils droit est NULL vers le nœud successeur (pour les nœuds dont le fils droit n'est pas nul, le fils droit est le nœud à visiter ensuite). De cette façon, pour n’importe quel nœud, après y avoir accédé, son fils droit a pointé vers le prochain nœud à visiter. Pour le nœud le plus à droite, aucune opération de ce type n’est requise. Notez que cette opération est terminée pendant le parcours et que l'arborescence sera restaurée après avoir terminé l'accès au nœud. La condition de jugement de toute la boucle est de savoir si le nœud actuel est vide. Par exemple, dans l'arbre binaire ci-dessus, le processus de parcours est le suivant (selon la position du nœud courant c) :

(1) Le nœud courant est 10, car le fils de gauche n'est pas vide et inaccessible. Recherchez le nœud le plus à droite du sous-arbre gauche de c p :

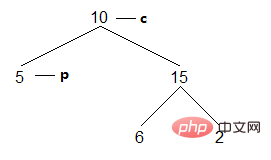
Résultat : []

(2) Il y en a deux. conditions de terminaison pour trouver le nœud le plus à droite du sous-arbre gauche du nœud c, un fils droit est vide, un fils droit pointe vers le nœud actuel. Voici le cas où le fils droit est vide. Ce cas doit d'abord être construit, en pointant le fils droit du nœud p vers le nœud successeur c, puis en déplaçant c vers le bas :

<🎜. >

Résultat : []

(3) Le fils gauche du nœud actuel c est vide et est accessible. Après l'accès, pointez c vers le bon fils (c'est-à-dire le nœud successeur) :

Résultat : [5]

(4) Continuer pour rechercher le sous-arbre de gauche Le nœud le plus à droite, cette fois la condition de terminaison est que le nœud le plus à droite soit le nœud actuel. Cela montre que le sous-arbre gauche du nœud actuel a été parcouru. Après avoir accédé au nœud actuel, restaurez l'arbre binaire et pointez le nœud actuel vers le nœud successeur :

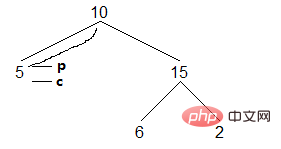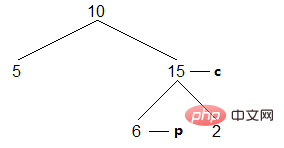
<. 🎜> Résultat : [5,10 ]

(5) Répétez le processus ci-dessus jusqu'à ce que c pointe vers le nœud le plus à droite de tout l'arbre binaire :

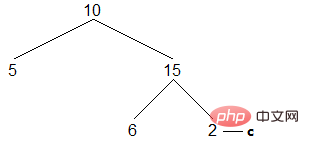
Le fils de gauche est vide, accès , c va au fils de droite. Le fils de droite est vide et ne remplit pas la condition de jugement. La boucle se termine et le parcours est terminé. Les résultats sont les suivants :

[5,10,6,15,2]

Il s'agit de la méthode Morris, avec une complexité temporelle de O(n) et une complexité spatiale de O (1). Le code est le suivant :

//Morris traversal,without a stack
class Solution3 {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        if(root==NULL)return ret;
        TreeNode *curr=root;
        TreeNode *pre;
        while(curr)
        {
            if(curr->left==NULL)
            {
                ret.push_back(curr->val);
                curr=curr->right;
            }
            else
            {
                pre=curr->left;
                while(pre->right&&pre->right!=curr)
                    pre=pre->right;
                if(pre->right==NULL)
                {
                    pre->right=curr;
                    curr=curr->left;
                }
                else
                {
                    ret.push_back(curr->val);
                    pre->right=NULL;
                    curr=curr->right;
                }
            }
        }
        return ret;
    }
};

Tutoriel recommandé : "

C#

"

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!