Récemment, je travaille sur une petite exigence. Chaque commande déterminera la valeur maximale des enveloppes rouges que l'utilisateur peut utiliser en fonction du montant. Si l'utilisateur choisit d'utiliser des enveloppes rouges, il doit l'aider à sélectionner le rouge optimal. combinaison d'enveloppes dans la liste des enveloppes rouges dont ils disposent. La combinaison requise La valeur de l'enveloppe rouge est la plus proche ou égale à la valeur maximale de l'enveloppe rouge pouvant être utilisée. Après y avoir réfléchi un moment, n'est-ce pas le « problème du sac à dos 0-1 » ? Je peux enfin mettre en pratique l'algorithme de « programmation dynamique » que j'ai appris auparavant !
La programmation dynamique (Abréviation de programmation dynamique : DP) est une méthode utilisée en mathématiques, sciences de gestion, informatique, économie et bioinformatique, en décomposant le problème initial en une méthode relativement simple pour résoudre des problèmes complexes. problèmes sous forme de sous-problèmes.
La programmation dynamique convient souvent aux problèmes comportant des sous-problèmes qui se chevauchent et des propriétés de sous-structure optimales. Les méthodes de programmation dynamique prennent souvent beaucoup moins de temps que les solutions naïves.
La programmation dynamique est généralement utilisée pour résoudre le problème de la recherche de la solution optimale. Dans le processus de résolution du problème, plusieurs décisions sont nécessaires, et chaque décision produit un ensemble d’états, puis la décision suivante continue à partir de la décision optimale pour finalement trouver le résultat optimal.
De plus, la programmation dynamique présente également 3 caractéristiques, comme suit :
Si la solution du sous-problème contenue dans la solution optimale du problème est également optimale, nous appelons le problème la sous-structure optimale propriétés (c’est-à-dire satisfaire le principe d’optimisation). Par conséquent, nous pouvons déduire la solution optimale du problème à travers la solution optimale du sous-problème. On peut également comprendre que l’état de l’étape ultérieure peut être déduit de l’état de l’étape précédente.
C'est-à-dire qu'une fois la solution à un sous-problème déterminée, elle ne changera plus et ne sera pas affectée par les solutions ultérieures au problème plus vaste qui l'inclut.
peut être simplement compris comme lors de la dérivation de l'état de l'étape suivante, nous n'avons qu'à nous soucier de l'état de l'étape précédente, et n'avons pas besoin de nous soucier de la façon dont cet état est dérivé étape par étape. Le deuxième sens est qu’une fois que le statut d’une certaine étape est déterminé, il ne sera pas affecté par les décisions des étapes ultérieures.
La nature imbriquée des sous-problèmes signifie que lorsqu'un algorithme récursif est utilisé pour résoudre un problème de haut en bas, les sous-problèmes générés à chaque fois ne sont pas toujours de nouveaux problèmes, et certains sous-problèmes seront calculés à plusieurs reprises
La théorie ci-dessus est relativement abstraite et tout comme un non-sens. Jetons un coup d'œil au problème du sac à dos classique.
Supposons qu'il y ait 5 articles et que leurs poids soient respectivement 2, 2, 5, 11, 4. Maintenant, il y a un sac à dos et le poids maximum qu'il peut supporter est 10 Veuillez choisir les articles appropriés à mettre dans le sac à dos. être combiné ?
Différentes combinaisons d'articles auront de nombreux états différents. Nous pouvons utiliser f(i, w) pour représenter un état, où i = index représente le numéro de l'article et w = weight représente le poids total actuel.
L'ensemble du problème doit être résolu en 『n』 étapes. Chaque étape nécessite une décision quant à savoir si un objet doit être mis dans le sac à dos. La décision n'a que deux résultats : "Mettez-le dedans" ou "Ne le mettez pas". ça dedans". Après avoir choisi un article, le poids de l'article dans le sac à dos aura de nombreux états différents. Nous devons fusionner les états répétitifs de chaque couche et ne laisser que les différents états. Ensuite, les résultats d'état de la couche suivante sont dérivés sur la base des résultats d'état de la couche précédente. En fin de compte, la solution de combinaison optimale peut être trouvée une fois que tous les éléments ont été décidés.
Le poids du 0ème élément (en fait le premier élément, commencez à souscrire à partir de 0 comme d'habitude) est de 2, puis commencez à décider s'il faut le mettre dans le sac à dos, il n'y a que 2 résultats. S'il est mis dans le sac à dos, le poids du sac à dos à ce moment est de 2. S'il n'est pas mis dans le sac à dos, le poids du sac à dos est de 0. Il est enregistré comme $status[0][0] = true ; $status[0][2] = truef(i, w)Le poids du premier article est toujours de 2, et ensuite nous commençons à prendre une décision à ce sujet. Il n'y a que deux choix pour la prise de décision : le mettre dans le sac à dos ou ne pas le mettre dans le sac à dos, mais il y en a beaucoup. combinaisons d’états car elles sont basées sur l’état précédent du sac à dos. Après avoir terminé la décision sur le premier élément, il y aura 3 états (en fait 4 états, mais s'il y a 1 doublon, il ne sera pas compté. Il sera toujours compté comme 3 états différents).
Si la décision est prise de mettre l'article actuel dans le sac à dos et que le 0ème article n'est pas mis dans le sac à dos, le statut à ce moment est $status[1][2 + 0] = true; => $status[1][2] = true Si la décision est prise de mettre l'article actuel dans le sac à dos, et le 0ème article est également mis dans le sac à dos, le statut à ce moment est $status[1][2 + 2] = true; => $status[1][4] = trueS'il est décidé de ne pas mettre l'article actuel dans le sac à dos et que le 0ème article n'est pas mis dans le sac à dos, le statut à ce moment est
;$status[1][0 + 0] = true; => $status[1][0] = true
où $status[1][0 + 2] = true; => $status[1][2] = true est répété, il y aura donc 3 résultats. .
$status[1][2]
Il en va de même pour les éléments suivants. Jusqu'à ce que tous les éléments aient été décidés, l'ensemble du tableau d'états a été trouvé, et il vous suffit ensuite de trouver la valeur maximale la plus proche avec une valeur true dans la dernière couche (In). dans l'exemple ci-dessus, la valeur 10) est la valeur maximale que peut supporter le sac à dos. Ensuite, vous pouvez avancer depuis la fin pour découvrir les indices d'éléments correspondants, c'est-à-dire quelle combinaison d'éléments constitue la combinaison de solutions optimale.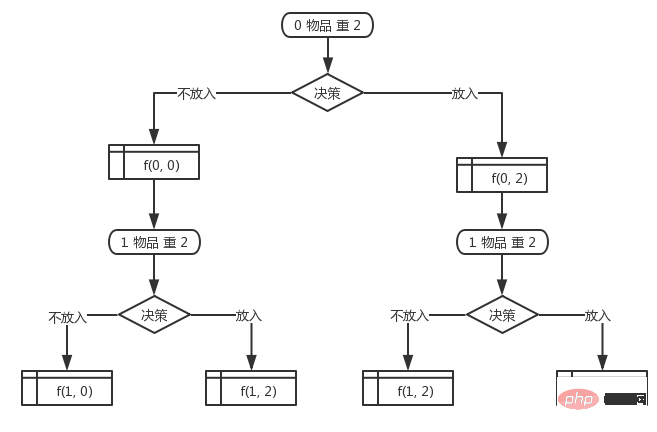 
En fait, le processus de dérivation ci-dessus est l'idée de résolution de problèmes de la programmation dynamique. Divisez le problème en étapes, chaque étape correspondant à une stratégie. Enregistrez ensuite l'état de chaque étape (attention à supprimer les doublons), puis déduisez-en tous les états possibles de l'étape suivante grâce aux possibilités de l'état actuel, et déduisez-le dynamiquement. 
function dynamicKnapsack($arr, $n, $max){
// 初始化二维数组
$status = [];
for ($i = 0; $i = 0; $j--) {
if ($status[$n - 1][$j] == true) {
break;
}
}
for ($i = $n - 1; $i >= 1; $i--) { // 外层遍历行
if ($j - $arr[$i] >= 0 && $status[$i - 1][$j - $arr[$i]] == 1) {
var_dump('buy this product: '.$arr[$i]);
$best[] = $i;
$j = $j - $arr[$i];
}
}
if ($j != 0) {
var_dump('buy first product:'.$arr[0]);
$best[] = 0;
}
return $best;}// 测试数据$arr = [
2, 2, 5, 11, 4,];$n = 5;$max = 10;$best = dynamicKnapsack($arr, $n, $max);var_dump($best);11
et que le résultat est une combinaison de, vous vous demandez peut-être s'il existe un autre résultat de 11. Cela se trouve être suffisant, n'est-ce pas ? Je pense que cela devrait dépendre des besoins réels. Par exemple, cette fois, mon exigence est de trier les enveloppes rouges par date d'expiration et d'utiliser en premier celles qui sont sur le point d'expirer. Ensuite, lors de l'assemblage des données, je force les enveloppes rouges qui sont sur le point d'expirer à la fin du tableau. dans l'ordre du délai d'expiration pour former un tableau. Puis le dernier 4 C'est l'enveloppe rouge qui est sur le point d'expirer. Je veux d'abord consommer cette enveloppe rouge. Si j'en utilise 4, je ne peux pas en utiliser 11. Je ne peux que continuer. cherchez-le devant. 4, 5, 2
La complexité spatiale est l'espace du tableau demandé au début O(n*max) plus l'accumulation des résultats de calcul peut se produire
O(n*max+1) De manière générale, il s'agit d'une idée d'échange d'espace contre du temps. De plus, si vous utilisez j pour passer de petit à grand dans la boucle imbriquée de la prise de décision intermédiaire, il y aura un problème de calculs répétés dans la boucle for. O(n*2*max)
Apprentissage recommandé : "
Tutoriel vidéo PHP"
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Comment ouvrir le fichier php
Comment supprimer les premiers éléments d'un tableau en php
Que faire si la désérialisation php échoue
Comment connecter PHP à la base de données mssql
Comment connecter PHP à la base de données mssql
Comment télécharger du HTML
Comment résoudre les caractères tronqués en PHP
Comment ouvrir des fichiers php sur un téléphone mobile
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
