Il existe de nombreuses variantes de cette légende et on ne sait pas de qui il s'agit, mais les problèmes mathématiques laissés derrière sont très classiques.
Les connaissances mathématiques qu'il a laissées : la relation entre le nombre de pièces d'or et le nombre de pas en mouvement est
.2^n - 1
2^64 - 1
L'algorithme de la Tour de Hanoï a deux conditions de base, en supposant que la plaque soit déplacée.
1. Une seule assiette peut être déplacée à la fois.
2. La petite assiette doit être au-dessus de la grande assiette.L'état initial est le suivant :
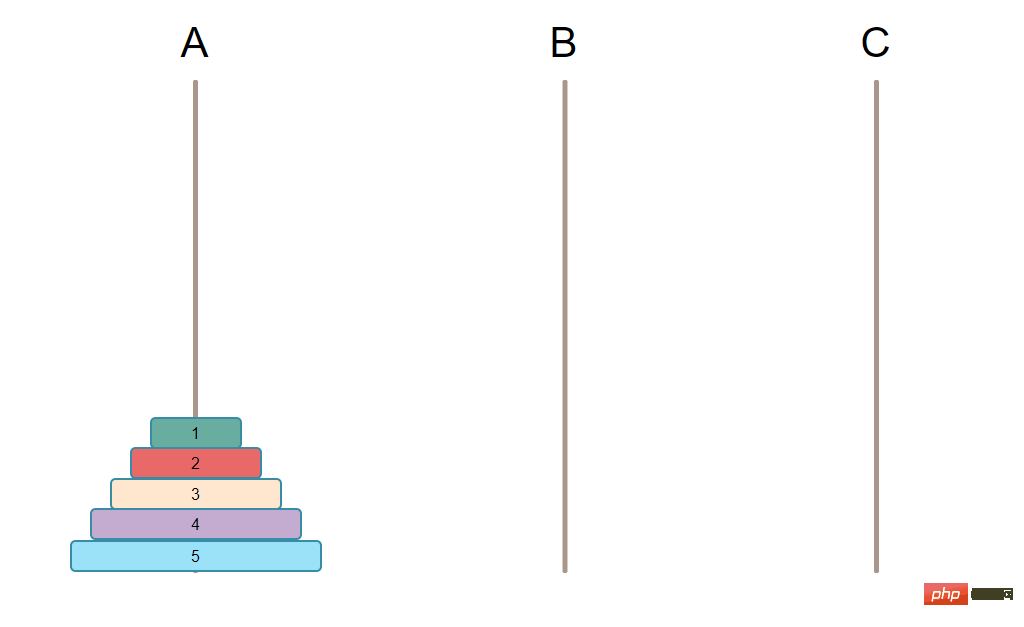Le but ultime à atteindre est de déplacer toutes les plaques d'un pilier vers un autre pilier. [Apprentissage recommandé :
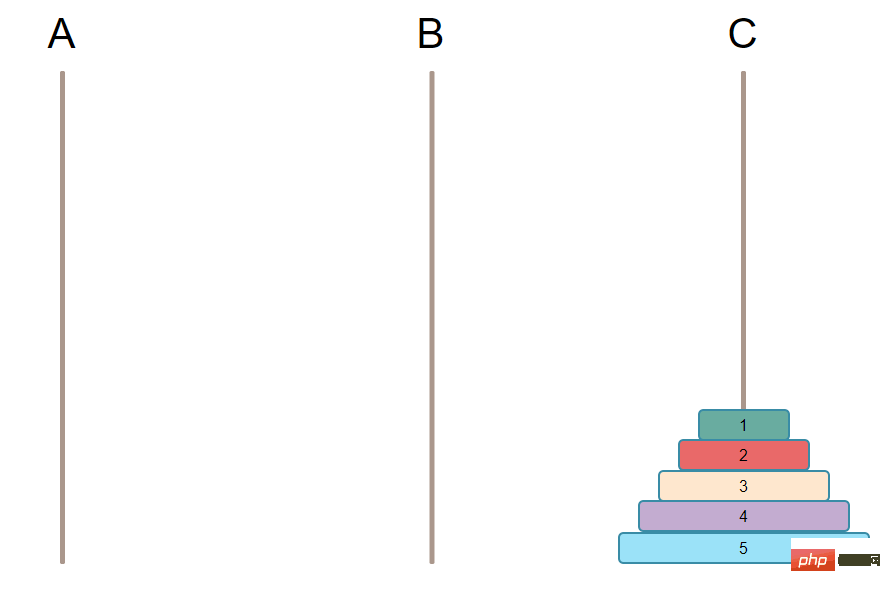Idée générale de mise en œuvre :
N-1Déplacez les N-1N-1Déplacez enfin ces plaques N-1 du pilier B vers le pilier C pour compléter l'objectif final. Pourquoi devons-nous d'abord déplacer N-1 vers B ? Vous voyez, parce que ce que vous réalisez finalement est de déplacer toutes les plaques de A vers C, l'ordre ne peut pas être modifié, il se peut seulement que les grandes soient en bas et les petites en haut. Ensuite, vous devez d'abord déplacer le plus grand vers C, sinon les conditions ne seront pas remplies.
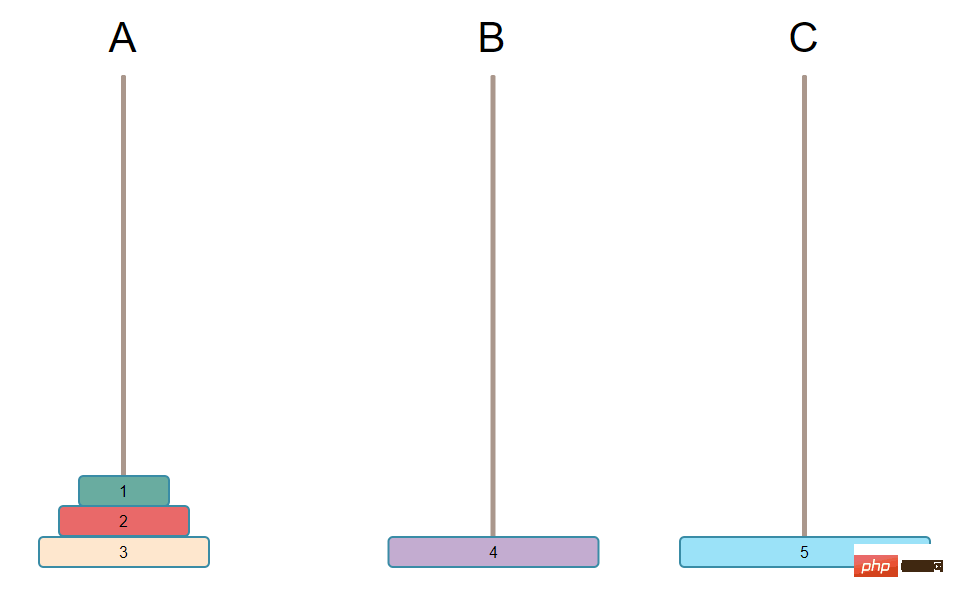
Pour déplacer la plus grande assiette de A à C, la plus grande assiette de A doit être libérée, c'est-à-dire que toutes les assiettes de la plus grande assiette doivent être déplacées. Et vous n'avez que 3 piliers. Il ne doit y avoir aucune autre poignée de plaque sur C, sinon vous ne remplirez plus les conditions. Toutes ces plaques N-1 ne peuvent être placées que sur B, et elles sont toujours en ordre. Cela devient l'image ci-dessous :
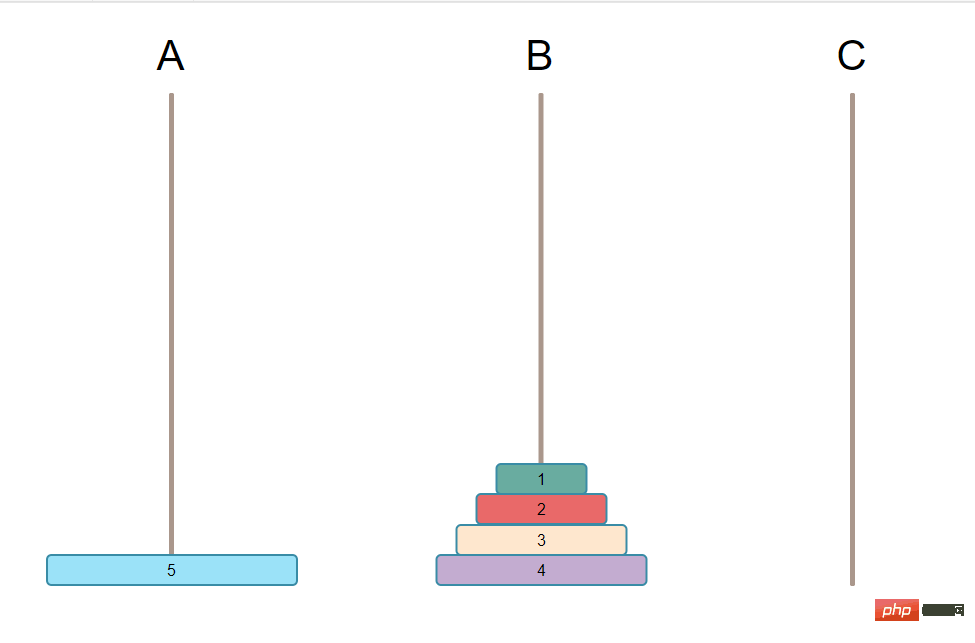
C'est très simple. Déplacez simplement la plus grande assiette de A à C en une seule étape. Comme indiqué ci-dessous : La troisième étape consiste à déplacer les plaques N-1 de B vers C. Remarque : Pour déplacer N-1 plaques vers C, cela revient-il à trouver la plus grande plaque parmi elles, puis à déplacer la plus grande plaque en premier ? Il s'agit donc ici de répéter les étapes 1 et 2, de trouver la plus grande parmi ces N-1 et de la déplacer en premier vers C, et le cycle se répète. La troisième étape équivaut en fait à modifier les exigences. Supposons que K = N - 1. devient l'image ci-dessous Trouvez d'abord la plus grande parmi les assiettes restantes puis déplacez la plus grande assiette Ensuite, faites une boucle jusqu'à ce qu'il ne reste qu'une seule assiette, passez directement à C, le jeu est terminé. Que sont les piliers auxiliaires ? Supposons que toutes les assiettes que vous souhaitez déplacer se trouvent sur A et que le but est de se déplacer vers C, alors B est le pilier auxiliaire de Ici, vous devez d'abord découvrir les piliers auxiliaires, ne réfléchissez pas à la manière de les mettre en œuvre, mais clarifiez d'abord la logique. Grâce à l'analyse ci-dessus, nous pouvons voir qu'il s'agit en fait d'une opération répétitive dans un cycle, très similaire à la récursivité, donc la récursivité peut être utilisée pour l'implémenter. Pour utiliser la récursion, il y a deux conditions nécessaires 1. Trouver la formule de récursion La condition de sortie est facile à écrire. Elle doit être déplacée directement vers le pilier C lorsqu'il n'y en a que. une assiette. Alors c'est quoi la formule de récidive ? Sur la base de l’analyse logique ci-dessus, elle peut être décomposée en 3 étapes. La première étape consiste à déplacer les [N-1] plaques de A à B Voici le pseudo-code implémenté en PHP: Les résultats sont les suivants: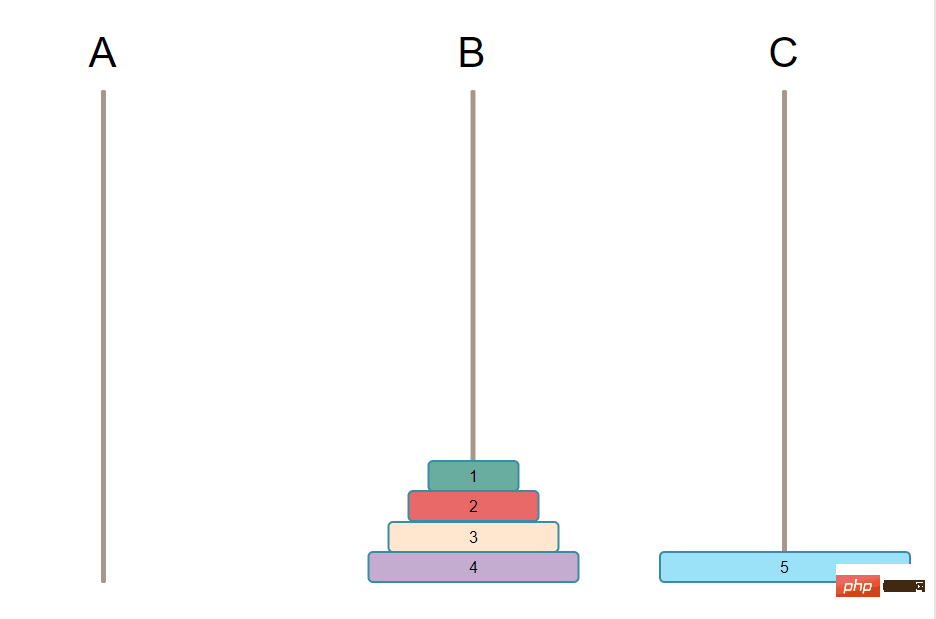
Il y a K assiettes sur le pilier B, le pilier A est vide, et le pilier C a la plus grande assiette, donc pour le pilier B avec K assiettes, cela équivaut à être vide.
La première étape consiste à déplacer les plaques K-1 de B vers A.
La deuxième étape consiste à déplacer la Kième plaque de B vers C.
La troisième étape consiste à déplacer les plaques K-1 de A vers C.
...
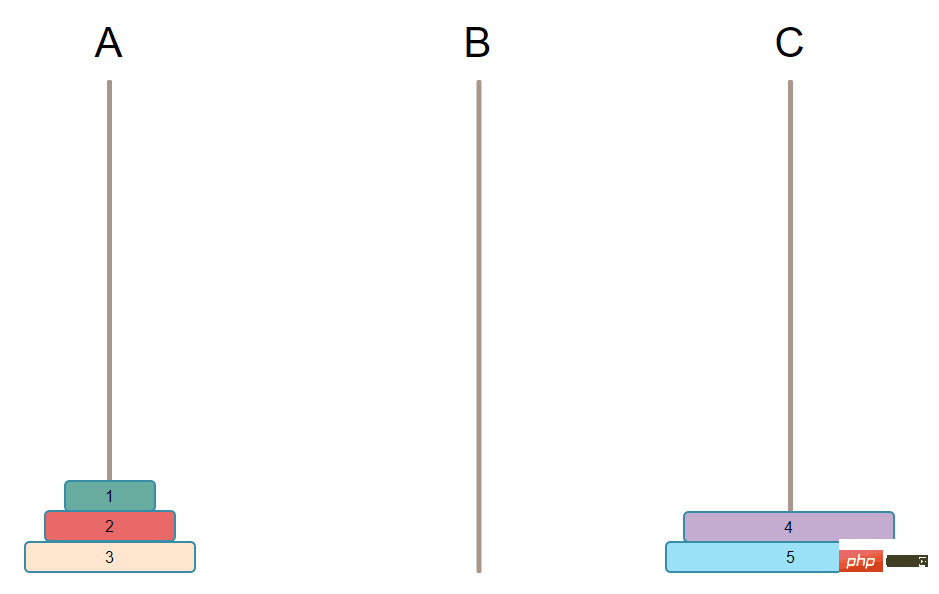
Piliers auxiliaires
N-1 assiettes. Parce qu’ils ne peuvent exister ici que temporairement, sinon ils ne respecteront pas les règles du jeu.
Implémentation
2 Trouver la condition de sortie
La deuxième étape consiste à déplacer la [Nième] plaque de A à C
La troisième étape consiste à déplacer la [Nième] plaque restant] -1 pièce] La plaque est déplacée de B vers Cclass HanoiTower
{
// 计数器
public $count = 0;
/**
* 汉诺塔实现
*
* @param $n 盘子号
* @param $A 初始柱子
* @param $B 中转站
* @param $C 目标柱子
*/
public function hanoi($n, $A, $B, $C)
{
if ($n == 1) {
// 退出条件 只剩一个盘子的时候直接从A移动到C
$this->biggestOne($n, $A, $B, $C);
} else {
// Analysez comment PHP implémente lintéressant algorithme de la Tour de Hanoï把 【n-1】 个盘子从A移动到B 此时C为中转站
$this->hanoi($n - 1, $A, $C, $B);
// Analysez comment PHP implémente lintéressant algorithme de la Tour de Hanoï把 【第n】 个盘子从A移动到C
$this->biggestOne($n, $A, $B, $C);
// 第三步把B上 【剩余的n-1个】 盘子从B移动到C 此时A为中转站
$this->hanoi($n - 1, $B, $A, $C);
}
}
/**
* 移动最大的盘子
* 直接从A移动到C
*/
public function biggestOne($n, $A, $B, $C)
{
++$this->count;
echo '第', $this->count, '步 ', '把 ', $n, '从 ', $A, '移动到', $C, '<br />';
}
}
$n = 5;
$hanoiTower = new HanoiTower();
echo '这是一个有 【', $n, '】 个盘子的汉诺塔：', '<br />';
// 调用执行
$hanoiTower->hanoi($n, 'A', 'B', 'C');
echo '总共需要走：【', $hanoiTower->count, '】 步';
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
Comment ouvrir le fichier php
Comment supprimer les premiers éléments d'un tableau en php
Que faire si la désérialisation php échoue
Comment connecter PHP à la base de données mssql
Comment connecter PHP à la base de données mssql
Comment télécharger du HTML
Comment résoudre les caractères tronqués en PHP
Comment ouvrir des fichiers php sur un téléphone mobile
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
