Quels sont les algorithmes de tri stables ?
Les algorithmes de tri stables incluent : 1. Tri par bulles ; 2. Tri par sélection ; 3. Tri par insertion ; 5. Tri par fusion ; 7. Tri par colline (shell) ;

L'environnement d'exploitation de ce tutoriel : système Windows 10, ordinateur Dell G3.
Analysez la stabilité des algorithmes de tri courants et donnez des raisons simples pour chacun.
Algorithme de tri stable :
1. Tri à bulles
Le tri à bulles consiste à déplacer les petits éléments vers l'avant ou les grands éléments vers l'arrière. La comparaison est une comparaison de deux éléments adjacents, et un échange se produit également entre ces deux éléments. Donc, si deux éléments sont égaux, je ne pense pas que vous les échangeriez de manière ennuyeuse.
Si deux éléments égaux ne sont pas adjacents, alors même si les deux sont adjacents lors de l'échange par paire précédent, ils ne seront pas échangés à ce moment-là, donc l'ordre des mêmes éléments n'a pas changé, donc le tri des bulles est une stabilité. algorithme de tri.
2. Tri par sélection
Le tri par sélection sélectionne le plus petit élément actuel pour chaque position, sélectionnez le plus petit pour la première position, sélectionnez le deuxième plus petit pour le deuxième élément parmi les éléments restants, et ainsi de suite. jusqu'à l'élément n-1, le n-ième élément n'a pas besoin d'être sélectionné, car c'est le seul plus grand élément restant. Ensuite, dans une sélection, si l'élément courant est plus petit qu'un élément, et que le petit élément apparaît après un élément égal à l'élément courant, alors la stabilité sera détruite après l'échange. n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了,所以选择排序不是一个稳定的排序算法。
3、插入排序
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。当然,刚开始这个有序的小序列只有1个元素,就是第一个元素。比较是从有序序列的末尾开始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。
如果碰见一个和插入元素相等的,那么插入元素把想插入的元素放在相等元素的后面。
所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
4、快速排序
快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[center_index],其中center_index是中枢元素的数组下标,一般取为数组第0个元素。而右边的j下标一直往左走,当a[j]>a[center_index]。
如果i和j都走不动了,i<=j,交换a[i]和a[j],重复上面的过程,直到i>j。交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为5 3 3 4 3 8 9 10 11,现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j] 交换的时刻。
5、归并排序
归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个序列(1次比较和交换),然后把各个有序的段序列合并成一个有序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2
5 8 5 2 9, on sait que sélectionner le 1ème élément 5 > dans la première passe correspondra Si 2 est échangé, l'ordre relatif de 2 et 5 dans la séquence d'origine sera détruit, donc la sélection le tri n'est pas un algorithme de tri stable.
3. Tri par insertion
Le tri par insertion insère un élément à la fois en fonction d'une petite séquence déjà ordonnée. Bien entendu, au début, cette petite séquence ordonnée ne comportait qu’un seul élément, qui était le premier élément. La comparaison commence à la fin de la séquence ordonnée, c'est-à-dire que l'élément que vous souhaitez insérer est comparé au plus grand déjà trié. S'il est plus grand que lui, insérez-le directement derrière lui, sinon continuez à regarder vers l'avant jusqu'à ce que vous ayez terminé. trouver l'élément dans lequel il doit être inséré.
Si vous rencontrez un élément égal à l'élément inséré, alors l'élément inséré placera l'élément que vous souhaitez insérer après l'élément égal. Ainsi, l'ordre des éléments égaux n'a pas changé. L'ordre de la séquence non ordonnée d'origine est l'ordre après le tri, donc le tri par insertion est stable. 🎜4. Tri rapide🎜🎜🎜Le tri rapide a deux directions. L'indice i à gauche va jusqu'à la droite. Lorsquea[i] <= a[center_index], où center_index est l'index du tableau de l'élément central, qui est généralement considéré comme l'élément 0 du tableau. L'indice j à droite va jusqu'à la gauche, lorsque a[j]>a[center_index]. 🎜🎜Si i et j ne peuvent pas marcher, i<=j, échangez a[i] et a[j], répétez Le processus ci-dessus se poursuit jusqu'à i>j. Échangez a[j] et a[center_index] pour effectuer un tri rapide. Lorsque l'élément pivot est échangé avec a[j], il est très probable que la stabilité de l'élément précédent soit perturbée. Par exemple, la séquence est 5 3 3 4 3 8 9. 10 11, maintenant les éléments hub 5 et 3 (l'élément 5, l'indice commence à partir de 1 code>) sont échangés Cela perturbera la stabilité de l'élément 3, le tri rapide est donc un algorithme de tri instable. L'instabilité se produit au moment où l'élément central et a[j] sont échangés. 🎜🎜🎜5. Tri par fusion🎜🎜🎜Le tri par fusion consiste à diviser la séquence de manière récursive en séquences courtes. La sortie récursive est que la séquence courte n'a que des éléments <code>1 (considérés comme étant directement ordonnés) ou <. code>2 code> séquences (comparaison et échange 1), puis fusionnez chaque séquence de segments ordonnés en une longue séquence ordonnée, et continuez la fusion jusqu'à ce que les séquences d'origine soient toutes triées. On constate que lorsqu'il y a des éléments 1 ou 2, les éléments 1 ne seront pas échangés, et 2 les éléments ne seront pas échangés si les tailles sont égales et que personne ne les échange intentionnellement, cela ne rompt pas la stabilité. 🎜🎜Donc, lors du processus de fusion de courtes séquences ordonnées, la stabilité est-elle détruite ? 🎜🎜Non, lors du processus de fusion nous pouvons garantir que si les deux éléments courants sont égaux, nous sauvegarderons l'élément de la séquence précédente devant la séquence résultat, assurant ainsi la stabilité. Par conséquent, le tri par fusion est également un algorithme de tri stable. 🎜🎜🎜6. Le tri Radix🎜🎜🎜Le tri Radix consiste à trier d'abord par ordre faible, puis à collecter 🎜🎜puis à trier par ordre élevé, puis à collecter ;Et ainsi de suite, jusqu'à la position la plus élevée. Parfois, certains attributs ont un ordre de priorité. Ils sont d'abord triés par priorité faible, puis par priorité élevée. L'ordre final est que ceux ayant une priorité élevée viennent en premier, et ceux ayant la même priorité élevée et faible viennent en premier. Le tri Radix est basé sur un tri séparé et une collecte séparée, il s'agit donc d'un algorithme de tri stable.
7. Tri en colline (coque)
Le tri en colline consiste à insérer et trier des éléments selon différentes longueurs de pas Lorsque les éléments sont très désordonnés au début, la taille du pas est la plus grande, donc le nombre d'éléments dans. le tri par insertion est très important, très rapide.
Lorsque les éléments sont essentiellement ordonnés et que la taille du pas est petite, le tri par insertion est très efficace pour les séquences ordonnées. Par conséquent, la complexité temporelle du tri Hill sera meilleure que O(n^2). En raison de plusieurs tris par insertion, nous savons qu'un tri par insertion est stable et ne modifiera pas l'ordre relatif des mêmes éléments. Cependant, dans différents processus de tri par insertion, les mêmes éléments peuvent se déplacer dans leurs tris par insertion respectifs, et finalement leur stabilité le sera. les changements sont brouillés, donc le tri des shells est instable. O(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
8、堆排序
我们知道堆的结构是节点i的孩子为2 * i和2 * i + 1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n的序列,堆排序的过程是从第n / 2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n / 2-1, n/2-2,...1这些个父节点选择元素时,就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1
i sont 2 * i et 2 * i + 1 nœud, un grand tas supérieur nécessite que le nœud parent soit supérieur ou égal à ses nœuds enfants 2, et un petit tas supérieur nécessite que le nœud parent soit inférieur ou égal à ses nœuds enfants 2. Dans une séquence de longueur n, le processus de tri des tas consiste à sélectionner la plus grande valeur à partir de n / 2 et ses nœuds enfants au total 3 (Grand tas supérieur) ou le plus petit (petit tas supérieur), le choix entre ces 3 éléments ne détruira certainement pas la stabilité. Mais lors de la sélection d'éléments pour les nœuds parents n/2-1, n/2-2, ...1, cela détruira la stabilité . Il est possible que le n/2ème nœud parent échange l'élément suivant, alors que le n/2-1ème nœud parent n'échange pas l'élément identique suivant, alors. la stabilité entre ces deux éléments identiques est détruite. Par conséquent, le tri par tas n’est pas un algorithme de tri stable. 🎜🎜Pour plus de connaissances connexes, veuillez visiter la rubrique 🎜FAQ🎜 ! 🎜Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Problèmes complexes de conception expérimentale sur le marché biface de Kuaishou
Apr 15, 2023 pm 07:40 PM
Problèmes complexes de conception expérimentale sur le marché biface de Kuaishou
Apr 15, 2023 pm 07:40 PM
1. Contexte du problème 1. Introduction à l'expérience du marché biface Le marché biface, c'est-à-dire une plateforme, comprend deux participants, producteurs et consommateurs, et les deux parties se promeuvent mutuellement. Par exemple, Kuaishou a un producteur vidéo et un consommateur vidéo, et les deux identités peuvent se chevaucher dans une certaine mesure. L'expérimentation bilatérale est une méthode expérimentale qui combine des groupes du côté des producteurs et des consommateurs. Les expériences bilatérales présentent les avantages suivants : (1) L'impact de la nouvelle stratégie sur deux aspects peut être détecté simultanément, tels que les changements dans le DAU du produit et le nombre de personnes téléchargeant des œuvres. Les plateformes bilatérales ont souvent des effets de réseau transversaux. Plus il y a de lecteurs, plus les auteurs seront actifs, et plus les auteurs seront actifs, plus les lecteurs suivront. (2) Le débordement et le transfert d'effet peuvent être détectés. (3) Aidez-nous à mieux comprendre le mécanisme d'action. L'expérience AB elle-même ne peut pas nous dire la relation entre la cause et l'effet, seulement.
 Comment filtrer et trier les données dans le développement de la technologie Vue
Oct 09, 2023 pm 01:25 PM
Comment filtrer et trier les données dans le développement de la technologie Vue
Oct 09, 2023 pm 01:25 PM
Comment filtrer et trier les données dans le développement de la technologie Vue Dans le développement de la technologie Vue, le filtrage et le tri des données sont des fonctions très courantes et importantes. Grâce au filtrage et au tri des données, nous pouvons rapidement interroger et afficher les informations dont nous avons besoin, améliorant ainsi l'expérience utilisateur. Cet article expliquera comment filtrer et trier les données dans Vue et fournira des exemples de code spécifiques pour aider les lecteurs à mieux comprendre et utiliser ces fonctions. 1. Filtrage des données Le filtrage des données fait référence au filtrage des données qui répondent aux exigences en fonction de conditions spécifiques. Dans Vue, on peut passer comp
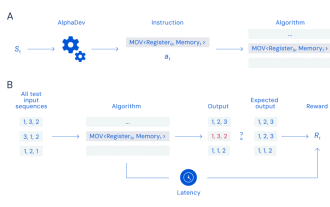 Google utilise l'IA pour briser le sceau de dix ans de l'algorithme de tri. Elle est exécutée des milliards de fois chaque jour, mais les internautes disent que c'est la recherche la plus irréaliste ?
Jun 22, 2023 pm 09:18 PM
Google utilise l'IA pour briser le sceau de dix ans de l'algorithme de tri. Elle est exécutée des milliards de fois chaque jour, mais les internautes disent que c'est la recherche la plus irréaliste ?
Jun 22, 2023 pm 09:18 PM
Tri | Nuka-Cola, Chu Xingjuan Les amis qui ont suivi des cours d'informatique de base doivent avoir personnellement conçu un algorithme de tri, c'est-à-dire utiliser du code pour réorganiser les éléments d'une liste non ordonnée par ordre croissant ou décroissant. C'est un défi intéressant, et il existe de nombreuses façons possibles de le relever. Beaucoup de temps a été investi pour trouver comment accomplir les tâches de tri plus efficacement. En tant qu'opération de base, les algorithmes de tri sont intégrés aux bibliothèques standard de la plupart des langages de programmation. Il existe de nombreuses techniques et algorithmes de tri différents utilisés dans les bases de code du monde entier pour organiser de grandes quantités de données en ligne, mais au moins en ce qui concerne les bibliothèques C++ utilisées avec le compilateur LLVM, le code de tri n'a pas changé depuis plus d'une décennie. . Récemment, l'équipe Google DeepMindAI a développé un
 Comment utiliser l'algorithme de tri par base en C++
Sep 19, 2023 pm 12:15 PM
Comment utiliser l'algorithme de tri par base en C++
Sep 19, 2023 pm 12:15 PM
Comment utiliser l'algorithme de tri par base en C++ L'algorithme de tri par base est un algorithme de tri non comparatif qui termine le tri en divisant les éléments à trier en un ensemble limité de chiffres. En C++, nous pouvons utiliser l’algorithme de tri par base pour trier un ensemble d’entiers. Ci-dessous, nous verrons en détail comment implémenter l'algorithme de tri par base, avec des exemples de code spécifiques. Idée d'algorithme L'idée de l'algorithme de tri par base est de diviser les éléments à trier en un ensemble limité de bits numériques, puis de trier les éléments sur chaque bit tour à tour. Le tri sur chaque bit est terminé
 Comment implémenter l'algorithme de tri par sélection en C#
Sep 20, 2023 pm 01:33 PM
Comment implémenter l'algorithme de tri par sélection en C#
Sep 20, 2023 pm 01:33 PM
Comment implémenter l'algorithme de tri par sélection en C# Le tri par sélection (SelectionSort) est un algorithme de tri simple et intuitif. Son idée de base est de sélectionner à chaque fois l'élément le plus petit (ou le plus grand) parmi les éléments à trier et de le placer à la fin de. la séquence triée. Répétez ce processus jusqu'à ce que tous les éléments soient triés. Apprenons-en davantage sur la façon d'implémenter l'algorithme de tri par sélection en C#, ainsi que des exemples de code spécifiques. Création d'une méthode de tri par sélection Tout d'abord, nous devons créer une méthode pour implémenter le tri par sélection. Cette méthode accepte un
 Swoole Advanced : Comment utiliser le multithreading pour implémenter un algorithme de tri à grande vitesse
Jun 14, 2023 pm 09:16 PM
Swoole Advanced : Comment utiliser le multithreading pour implémenter un algorithme de tri à grande vitesse
Jun 14, 2023 pm 09:16 PM
Swoole est un framework de communication réseau hautes performances basé sur le langage PHP. Il prend en charge la mise en œuvre de plusieurs modes IO asynchrones et de plusieurs protocoles réseau avancés. Sur la base de Swoole, nous pouvons utiliser sa fonction multi-threading pour implémenter des opérations algorithmiques efficaces, telles que des algorithmes de tri à grande vitesse. L'algorithme de tri à grande vitesse (QuickSort) est un algorithme de tri courant. En localisant un élément de référence, les éléments sont divisés en deux sous-séquences. Celles plus petites que l'élément de référence sont placées à gauche et celles supérieures ou égales à la référence. L'élément est placé à droite. Ensuite, les sous-séquences gauche et droite sont placées par récursion.
 Quels sont les algorithmes de tri des tableaux ?
Jun 02, 2024 pm 10:33 PM
Quels sont les algorithmes de tri des tableaux ?
Jun 02, 2024 pm 10:33 PM
Les algorithmes de tri de tableaux sont utilisés pour organiser les éléments dans un ordre spécifique. Les types courants d'algorithmes incluent : Tri à bulles : échangez les positions en comparant les éléments adjacents. Tri par sélection : recherchez le plus petit élément et remplacez-le par la position actuelle. Tri par insertion : insérez les éléments un par un à la bonne position. Tri rapide : méthode diviser pour mieux régner, sélectionnez l'élément pivot pour diviser le tableau. Tri par fusion : diviser pour mieux régner, tri récursif et fusion de sous-tableaux.
 Discussion sur les scénarios d'application de différents algorithmes de tri de tableaux PHP
Apr 28, 2024 am 09:39 AM
Discussion sur les scénarios d'application de différents algorithmes de tri de tableaux PHP
Apr 28, 2024 am 09:39 AM
Pour différents scénarios, il est crucial de choisir l’algorithme de tri des tableaux PHP approprié. Le tri à bulles convient aux tableaux à petite échelle sans exigences de stabilité ; le tri rapide a la complexité temporelle la plus faible dans la plupart des cas ; le tri par fusion a une stabilité élevée et convient aux scénarios qui nécessitent des résultats stables ; le tri par sélection convient aux situations sans exigences de stabilité. Le tri par tas trouve efficacement la valeur maximale ou minimale. Grâce à la comparaison de cas réels, le tri rapide est supérieur aux autres algorithmes en termes d'efficacité temporelle, mais le tri par fusion doit être choisi lorsque la stabilité doit être prise en compte.





