Parlons en profondeur de la raison pour laquelle l'index mysql utilise la structure arborescente B+

Cet article est une étude avancée de mysql Il présente la raison pour laquelle MySQL utilise l'arbre B+ comme structure de données d'index. J'espère qu'il sera utile à tout le monde !

L'index améliore l'efficacité des requêtes. Tout comme le livre que nous lisons, si nous voulons passer directement à un certain chapitre, nous n'avons pas besoin de tourner page par page. et trouvez le numéro de page en fonction de la table des matières. [Recommandations associées : Tutoriel vidéo MySQL]

Dans l'ordinateur, nous avons besoin d'une structure de données pour stocker ce répertoire. Les structures de données courantes incluent les tables de hachage, les arbres de recherche binaires, les arbres binaires équilibrés (AVL) et les arbres rouge-noir. alors pourquoi Innodb et MyISAM choisissent l'arbre b+.

1. Table de hachage

Une table de hachage est un tableau + liste chaînée, avec les indices 0, 1, 2, 3..... indiquant l'emplacement de ses données. Si vous souhaitez stocker des données dans une table de hachage, utilisez d'abord un algorithme de hachage sur les données (l'algorithme de base est l'opération modulo). Si la longueur du tableau est de 13, après modulo 13, elle sera de 0 à 12, ce qui correspond à). la partie inférieure des données. Si les indices calculés sont les mêmes, la liste chaînée suivra la position de l'indice.

Inconvénients :

1. L'utilisation du stockage par hachage nécessite l'ajout de tous les fichiers de données à la mémoire, ce qui consomme plus d'espace mémoire.
2. La recherche de hachage est une requête équivalente, qui est très rapide, mais il n'y a pas de règle de plage entre chaque donnée. Cependant, dans le travail réel, davantage de requêtes de plage sont utilisées et le hachage ne convient pas.

On ne peut pas dire directement que MySQL n'utilise pas de tables de hachage, mais cela doit être déterminé en fonction du moteur de stockage. Le moteur de stockage Memory utilise des tables de hachage

2.

Comme le montre l'image, dans des cas extrêmes, le problème d'inclinaison peut survenir, et finalement cela devient une structure de liste chaînée.

Les nœuds de l'arbre sont trop profonds, ce qui augmente l'IO de la recherche, et maintenant l'IO est le goulot d'étranglement de la recherche

1. 3 Arbre binaire équilibré-AVL
2. Afin de maintenir l'équilibre de l'arbre et d'éviter. biais des données, une opération de rotation est nécessaire, par rotation à gauche ou à droite, la longueur du sous-arbre le plus long et du sous-arbre le plus court ne peut pas dépasser 1. Si elle dépasse 1, ce n'est pas un arbre AVL au sens strict

Inconvénients :

1. Lorsque la quantité de données est importante, afin de maintenir l'équilibre, des rotations de 1 à n sont nécessaires. Cette rotation est un gaspillage de performances. L'efficacité de l'insertion et de la suppression est extrêmement faible et l'efficacité des requêtes est très élevée.

Avec seulement deux branches, la profondeur de l'arbre est encore très profonde lorsque la quantité de données est importante.

4. Arbre rouge-noir

2. Le sous-arbre le plus long ne peut pas dépasser 2 fois le sous-arbre le plus court. Grâce au changement de couleur et à la rotation, l'insertion et la requête sont équilibrées

L'arbre rouge-noir est une variante de l'arbre avl, qui perd les performances des requêtes partielles pour améliorer les performances d'insertion.

Inconvénients :

Il n'y a également que deux branches, et la profondeur sera toujours très profonde lorsque la quantité de données est importante

Avec l'augmentation des données, les trois types d'arbres binaires ci-dessus finiront par ont trop de nœuds. Et ils n'ont que 2 branches, donc le nombre d'IO est également important

Comment résoudre le problème qu'il n'y a que 2 branches et que la profondeur est trop profonde, donc il y a un B-tree. , ajoutez des branches

5. B-Tree

D'abord, ne lisez pas l'arbre B-soustrait, lisez le B-tree

Toutes les valeurs clés sont distribuées dans l'arbre entier.

La recherche peut se terminer à un nœud non-feuille, et une recherche est effectuée dans l'ensemble des mots-clés, et les performances sont proches de la recherche binaire.
1. Chaque nœud a au plus m sous-arbres.
2. Le nœud racine a au moins 2 sous-arbres.
3. Un nœud de branche a au moins m/2 sous-arbres (tous les nœuds de branche à l'exception du nœud racine et des nœuds feuilles).
4. Tous les nœuds feuilles sont sur le même calque, chaque nœud peut avoir jusqu'à m-1 clés et est disposé par ordre croissant

Comme le montre l'image ci-dessus : (Seule une partie de l'image est tiré, en fait il n'y a pas de limite, Plus de p1, p2, p3)

Chaque nœud occupe un bloc de disque. Il y a deux mots-clés disposés par ordre croissant sur un nœud et trois pointeurs vers le nœud racine du sous-arbre. Les pointeurs stockent l'adresse du bloc de disque où se trouve le nœud enfant. Les trois champs range divisés par les deux mots-clés correspondent aux champs range des données du sous-arbre pointé par les trois pointeurs. En prenant le nœud racine comme exemple, les mots-clés sont 16 et 34. La plage de données du sous-arbre pointé par le pointeur p1 est inférieure à 16, la plage de données du sous-arbre pointé par le pointeur p2 est 16-34 et les données La plage du sous-arbre pointé par le pointeur p3 est supérieure à 34. .

Le processus de recherche du mot-clé 28 :

1. trouver le bloc disque 1 basé sur le nœud racine et le lire dans la mémoire. [Première opération d'E/S disque]
2. Comparez le mot-clé 28 dans l'intervalle (16, 34) et recherchez le pointeur p2 du bloc de disque 1.
3. Trouvez le bloc disque 3 selon le pointeur p2 et lisez-le dans la mémoire. [Deuxième opération d'E/S disque]
4. Comparez le mot-clé 28 dans l'intervalle (25, 31) et recherchez le pointeur p2 du bloc de disque 3.
5. Trouvez le bloc disque 8 basé sur le pointeur p2 et lisez-le en mémoire. [La troisième opération d'E/S disque]
6. Trouvez le mot-clé 28 dans la liste de mots-clés du bloc de disque 8, fin.

Inconvénients : 

1. Chaque nœud possède une clé et contient également des données, et l'espace de stockage de chaque page est limité si les données sont volumineuses, le nombre de clés que chaque nœud peut stocker deviendra plus petit.
2. Lorsque la quantité de données stockées est importante, la profondeur augmente, augmentant le nombre de requêtes IO sur le disque et affectant ainsi les performances des requêtes.

6. Arbre B+

L'arbre B+ est une optimisation basée sur l'arbre B. Les changements sont les suivants :

1. Chaque nœud de l'arbre B+ peut contenir plus de nœuds. Il y a deux raisons à cela, la première raison. est de réduire la hauteur de l'arborescence, et la deuxième raison est de modifier la plage de données en plusieurs intervalles. Plus il y a d'intervalles, plus la récupération des données est rapide.
2. Les nœuds non-feuilles stockent uniquement les clés, et les nœuds feuilles stockent les clés et les données.
3. Les pointeurs des nœuds feuilles sont connectés les uns aux autres (conformément aux caractéristiques de lecture anticipée du disque) et les performances des requêtes séquentielles sont plus élevées.

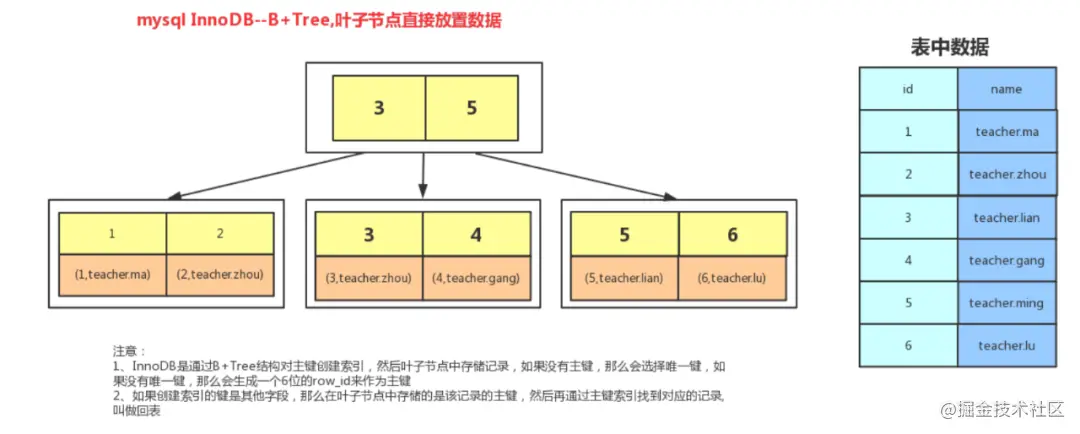
Comme le montre l'image ci-dessus : Il y a deux pointeurs de tête sur l'arborescence B+, l'un pointe vers le nœud racine et l'autre vers le nœud feuille minimum du mot-clé, et il y a une structure en anneau de chaîne entre tous les nœuds feuilles (et nœuds de données), donc le B+ L'arbre peut être Il existe trois opérations de recherche : l'une est une recherche par plage et une recherche par pagination de la clé primaire, et l'autre est une recherche aléatoire à partir du nœud racine.

Différences dans les index entre InnoDB et MyISAM

1. Index de clé primaire InnoDB

Les nœuds feuilles stockent des données de ligne spécifiques

2. Index de clé non primaire InnoDB

Stockage de nœud feuille de clé non primaire. index est la valeur de la clé primaire (les données de la requête doivent donc être renvoyées à la table)

3 MyISAM

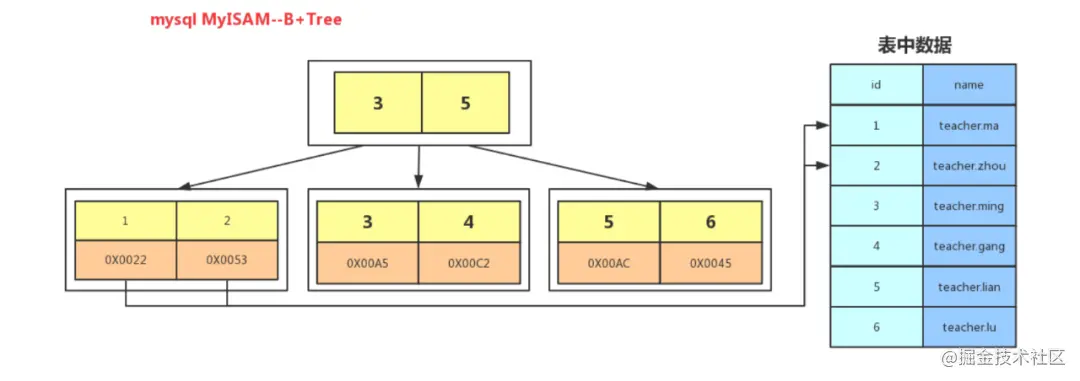
Les nœuds feuilles stockent l'adresse des données de ligne, ce qui nécessite un adressage supplémentaire et une IO supplémentaire.

Résumé : Pourquoi MySQL utilise l'arbre B+

Déclaration précise : Pourquoi les index des moteurs de stockage InnoDB et MyISAM de MySQL utilisent l'arbre B+

• La requête équivalente est rapide, mais pas elle satisfait les recherches de plage commune et il n'y a aucune relation entre deux valeurs adjacentes, et le hachage consomme plus de mémoire.

• Arbre binaire/arbre binaire équilibré/arbre rouge-noir, etc. ont tous et n'ont que 2 branches. Le point commun est que lorsque la quantité de données est grande, la profondeur de l'arbre devient plus profonde et le nombre. des IO est augmenté.

• B-tree stockera des données sur les nœuds, donc le nombre de clés stockées sur une page sera réduit et la profondeur de l'arborescence sera augmentée.

• Les données sont supprimées des nœuds non-feuilles dans l'arborescence B+, ce qui augmente le nombre de clés sur une page, et les nœuds feuilles sont connectés via des listes chaînées, ce qui est propice à la recherche de plage et à la pagination.

Adresse originale : https://juejin.cn/post/6994810803643744269

Auteur : M. Ji

Pour plus de connaissances liées à la programmation, veuillez visiter : Vidéo de programmation ! !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!