 interface Web
interface Web
 Questions et réponses frontales
Questions et réponses frontales
 JavaScript prend-il en charge les fonctions trigonométriques ?
JavaScript prend-il en charge les fonctions trigonométriques ?
JavaScript prend-il en charge les fonctions trigonométriques ?
JavaScript prend en charge les fonctions trigonométriques. Les fonctions trigonométriques en js sont toutes des méthodes statiques et doivent être appelées en utilisant Math, le format de syntaxe est donc "Math.sin(x)", "Math.cos(x)", "Math.tan(x)".

L'environnement d'exploitation de ce tutoriel : système Windows 7, JavaScript version 1.8.5, ordinateur Dell G3.
JavaScript prend en charge les fonctions trigonométriques. Ils sont : "Math.sin(x)", "Math.cos(x)", "Math.tan(x)".
Jetons un coup d'œil à la prise en charge par JavaScript des fonctions trigonométriques.
Tout d'abord, passons en revue les connaissances de base sur les fonctions trigonométriques que nous avons apprises au lycée. Je vais en présenter ici quelques-unes simples. La première est la fonction sin, la seconde est la fonction cos et la troisième est la fonction tan. fonction. Quatre ou quatre est la fonction atan. En mathématiques, la fonction sin est en fait la valeur obtenue en comparant les côtés opposés d'un triangle à l'hypoténuse. Regardons une image
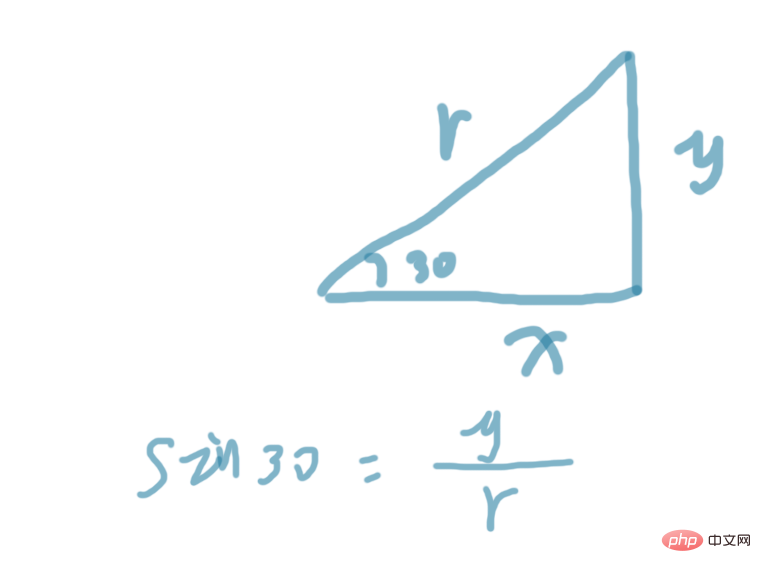
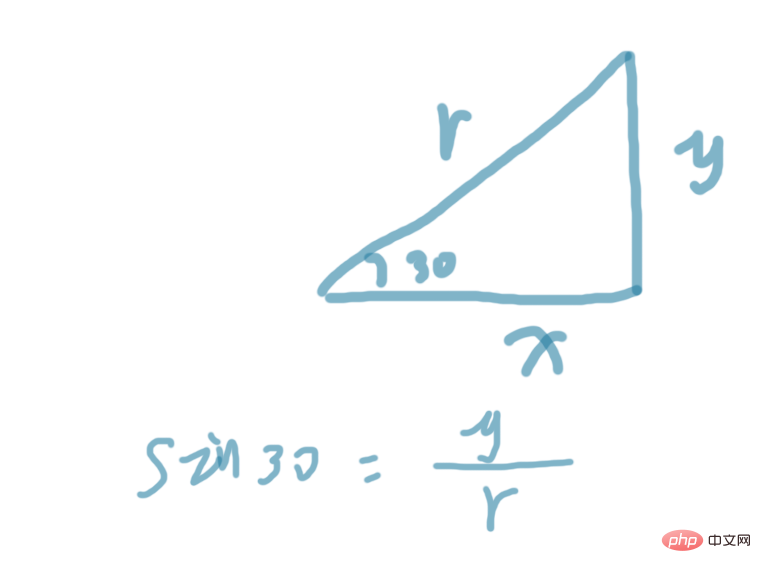
Alors cos30=. x/r code>, la fonction cos est le rapport du côté opposé au côté supérieur, <code>tan30=y/x, et la fonction tan est le rapport du côté opposé au côté supérieur. Côté. Grâce à ces formules, nous pouvons facilement obtenir les valeurs de cette fonction trigonométrique, et vous pouvez ensuite utiliser ces valeurs pour faire des choses intéressantes ! ! cos30=x/r,cos函数是临边比上斜边,tan30=y/x,tan函数则是对边比上临边,通过这些公式,我们可以很容易的得到这个三角函数的值,然后就阔以拿这些值去做有意思的事情啦!!
那么我们在javascript里面的三角函数和数学中的三角函数其实有一点区别外,第一是写发上不一样,js里面三角函数都是静态方法,必须使用Math来调用,三个函数分别是Math.sin(),Math.cos(),Math.tan()。
这个很容易理解咯,那么第二个不同就是数学里面的三角函数使用接受的参数是角度,但是在js里面所接受的参数是弧度,有的朋友可能晕了,弧度角度什么玩意???不要着急,这里简单介绍一下,我们首先来看一个圆
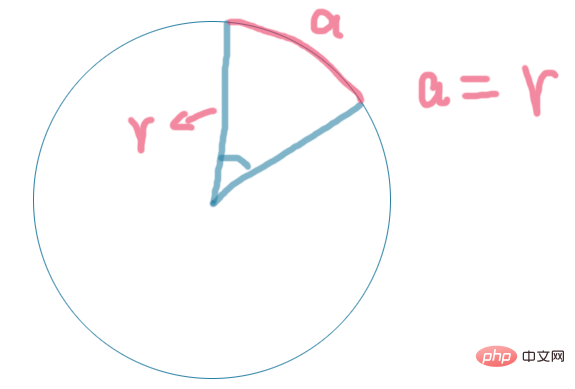
如果一个圆的一段边的长度等于这个圆的半径长度,那么这段边就代表一弧度,正如图中红色部分,就代表一弧度,这个其实仅仅就是一个概念,我们真正要使用的是吧我们想要的角度转化成弧度,这里直接套用数学公公式 1角度=π/180 那么10个角度就等于10*π/180啦
那我们要用js的Math.sin()算出30度角等于多少,那么就应该写成Math.sin(30*Math.PI/180),这里注意一下js里面的π是Math.PI
Math.sin(), Math.cos(), Math.tan(). C'est facile à comprendre. La deuxième différence est que les paramètres acceptés par les fonctions trigonométriques en mathématiques sont des angles, mais les paramètres acceptés en js sont des radians. Certains amis peuvent être confus. ? ? Ne vous inquiétez pas, voici une brève introduction. Regardons d'abord un cercle
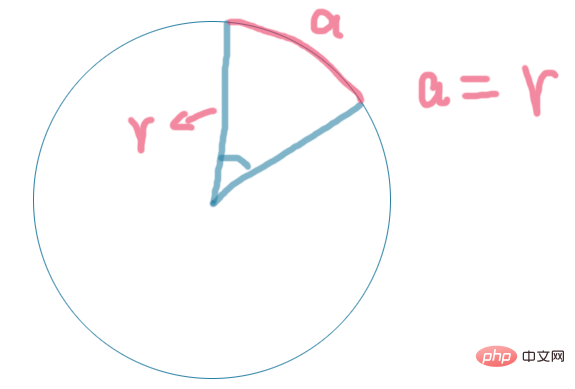
Si la longueur d'un côté d'un cercle est égale au rayon du cercle, alors ce côté représente un radian. Tout comme la partie rouge sur l'image, il représente un radian. juste un concept. Ce que nous voulons vraiment Ce que nous utilisons est de convertir l'angle que nous voulons en radians. Ici, nous appliquons directement la formule mathématique 1 angle=π/180 Ensuite, 10 angles sont égaux à . 10*π/180 La
Ensuite, nous devons utiliser Math.sin() de js pour calculer l'angle de 30 degrés, alors il doit être écrit comme Math.sin (30*Math.PI/180), veuillez noter ici que π en js est Math.PI. Je pense que tout le monde ici doit avoir une certaine compréhension des fonctions trigonométriques de js, jetons donc un coup d'œil à un petit exemple pratique.
Tout d’abord, il y a un besoin. Il y a une petite boule sur la page. Je veux que ma souris s'y déplace lorsque ma souris est placée sur la page. La balle se déplacera vers la position correspondante. Notez qu'elle ne se déplacera pas vers la position de la souris, mais vers la position correspondante. Il n'est pas facile de publier l'URL ici. 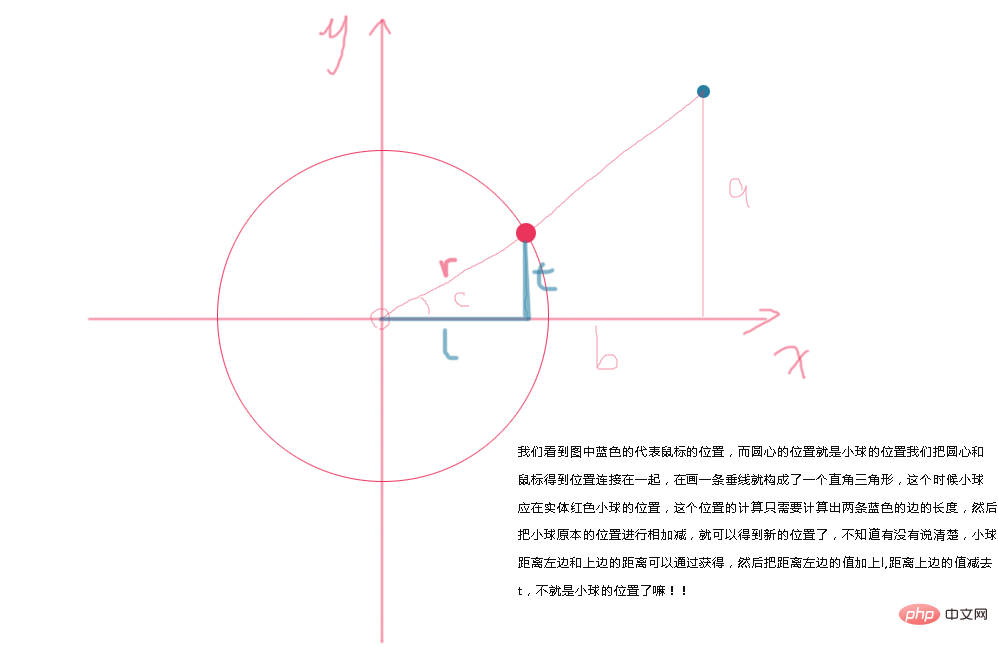
/***********例子来了*************/
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN" "http://www.w3.org/TR/html4/loose.dtd">
<html>
<head>
<meta http-equiv="Content-Type" content="text/html;charset=UTF-8">
<title>Document</title>
<style>
#box{width:30px;height:30px;background:red;position:absolute;top:400px;left:400px;border-radius:15px;}
</style>
</head>
<body>
<p id="box"></p>
</body>
<script>
var obox = document.getElementById('box');
var r=50;
document.onmousemove=function(ev){
var oev = ev||event;
var x = Math.abs(oev.clientX-obox.offsetLeft);
var y = Math.abs(oev.clientY-obox.offsetTop);
var angle = Math.atan(y/x);
var cx=0;
var cy=0;
if(oev.clientX>=obox.offsetLeft && oev.clientY<=obox.offsetTop){
cx = Math.cos(angle)*r;
cy = Math.sin(angle)*-r;
}
if(oev.clientX<obox.offsetLeft && oev.clientY<obox.offsetTop){
cx = Math.cos(angle)*-r;
cy = Math.sin(angle)*-r;
}
if(oev.clientX<obox.offsetLeft && oev.clientY>obox.offsetTop){
cx = Math.cos(angle)*-r;
cy = Math.sin(angle)*r;
}
if(oev.clientX>obox.offsetLeft && oev.clientY>obox.offsetTop){
cx = Math.cos(angle)*r;
cy = Math.sin(angle)*r;
}
obox.style.top = 400+cy+'px';
obox.style.left = 400+cx+'px';
}
</script>
</html>Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment mettre en œuvre un système de reconnaissance vocale en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 pm 02:54 PM
Comment mettre en œuvre un système de reconnaissance vocale en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 pm 02:54 PM
Comment utiliser WebSocket et JavaScript pour mettre en œuvre un système de reconnaissance vocale en ligne Introduction : Avec le développement continu de la technologie, la technologie de reconnaissance vocale est devenue une partie importante du domaine de l'intelligence artificielle. Le système de reconnaissance vocale en ligne basé sur WebSocket et JavaScript présente les caractéristiques d'une faible latence, d'un temps réel et d'une multiplateforme, et est devenu une solution largement utilisée. Cet article explique comment utiliser WebSocket et JavaScript pour implémenter un système de reconnaissance vocale en ligne.
 WebSocket et JavaScript : technologies clés pour mettre en œuvre des systèmes de surveillance en temps réel
Dec 17, 2023 pm 05:30 PM
WebSocket et JavaScript : technologies clés pour mettre en œuvre des systèmes de surveillance en temps réel
Dec 17, 2023 pm 05:30 PM
WebSocket et JavaScript : technologies clés pour réaliser des systèmes de surveillance en temps réel Introduction : Avec le développement rapide de la technologie Internet, les systèmes de surveillance en temps réel ont été largement utilisés dans divers domaines. L'une des technologies clés pour réaliser une surveillance en temps réel est la combinaison de WebSocket et de JavaScript. Cet article présentera l'application de WebSocket et JavaScript dans les systèmes de surveillance en temps réel, donnera des exemples de code et expliquera leurs principes de mise en œuvre en détail. 1. Technologie WebSocket
 Comment utiliser JavaScript et WebSocket pour mettre en œuvre un système de commande en ligne en temps réel
Dec 17, 2023 pm 12:09 PM
Comment utiliser JavaScript et WebSocket pour mettre en œuvre un système de commande en ligne en temps réel
Dec 17, 2023 pm 12:09 PM
Introduction à l'utilisation de JavaScript et de WebSocket pour mettre en œuvre un système de commande en ligne en temps réel : avec la popularité d'Internet et les progrès de la technologie, de plus en plus de restaurants ont commencé à proposer des services de commande en ligne. Afin de mettre en œuvre un système de commande en ligne en temps réel, nous pouvons utiliser les technologies JavaScript et WebSocket. WebSocket est un protocole de communication full-duplex basé sur le protocole TCP, qui peut réaliser une communication bidirectionnelle en temps réel entre le client et le serveur. Dans le système de commande en ligne en temps réel, lorsque l'utilisateur sélectionne des plats et passe une commande
 Comment mettre en œuvre un système de réservation en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 am 09:39 AM
Comment mettre en œuvre un système de réservation en ligne à l'aide de WebSocket et JavaScript
Dec 17, 2023 am 09:39 AM
Comment utiliser WebSocket et JavaScript pour mettre en œuvre un système de réservation en ligne. À l'ère numérique d'aujourd'hui, de plus en plus d'entreprises et de services doivent fournir des fonctions de réservation en ligne. Il est crucial de mettre en place un système de réservation en ligne efficace et en temps réel. Cet article explique comment utiliser WebSocket et JavaScript pour implémenter un système de réservation en ligne et fournit des exemples de code spécifiques. 1. Qu'est-ce que WebSocket ? WebSocket est une méthode full-duplex sur une seule connexion TCP.
 JavaScript et WebSocket : créer un système efficace de prévisions météorologiques en temps réel
Dec 17, 2023 pm 05:13 PM
JavaScript et WebSocket : créer un système efficace de prévisions météorologiques en temps réel
Dec 17, 2023 pm 05:13 PM
JavaScript et WebSocket : Construire un système efficace de prévisions météorologiques en temps réel Introduction : Aujourd'hui, la précision des prévisions météorologiques revêt une grande importance pour la vie quotidienne et la prise de décision. À mesure que la technologie évolue, nous pouvons fournir des prévisions météorologiques plus précises et plus fiables en obtenant des données météorologiques en temps réel. Dans cet article, nous apprendrons comment utiliser la technologie JavaScript et WebSocket pour créer un système efficace de prévisions météorologiques en temps réel. Cet article démontrera le processus de mise en œuvre à travers des exemples de code spécifiques. Nous
 Comment utiliser insertBefore en javascript
Nov 24, 2023 am 11:56 AM
Comment utiliser insertBefore en javascript
Nov 24, 2023 am 11:56 AM
Utilisation : En JavaScript, la méthode insertBefore() est utilisée pour insérer un nouveau nœud dans l'arborescence DOM. Cette méthode nécessite deux paramètres : le nouveau nœud à insérer et le nœud de référence (c'est-à-dire le nœud où le nouveau nœud sera inséré).
 Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript simple : Comment obtenir le code d'état HTTP
Jan 05, 2024 pm 06:08 PM
Tutoriel JavaScript : Comment obtenir le code d'état HTTP, des exemples de code spécifiques sont requis Préface : Dans le développement Web, l'interaction des données avec le serveur est souvent impliquée. Lors de la communication avec le serveur, nous devons souvent obtenir le code d'état HTTP renvoyé pour déterminer si l'opération a réussi et effectuer le traitement correspondant en fonction de différents codes d'état. Cet article vous apprendra comment utiliser JavaScript pour obtenir des codes d'état HTTP et fournira quelques exemples de codes pratiques. Utilisation de XMLHttpRequest
 JavaScript et WebSocket : créer un système de traitement d'images en temps réel efficace
Dec 17, 2023 am 08:41 AM
JavaScript et WebSocket : créer un système de traitement d'images en temps réel efficace
Dec 17, 2023 am 08:41 AM
JavaScript est un langage de programmation largement utilisé dans le développement Web, tandis que WebSocket est un protocole réseau utilisé pour la communication en temps réel. En combinant les puissantes fonctions des deux, nous pouvons créer un système efficace de traitement d’images en temps réel. Cet article présentera comment implémenter ce système à l'aide de JavaScript et WebSocket, et fournira des exemples de code spécifiques. Tout d’abord, nous devons clarifier les exigences et les objectifs du système de traitement d’images en temps réel. Supposons que nous disposions d'un appareil photo capable de collecter des données d'image en temps réel.





