 développement back-end
développement back-end
 tutoriel php
tutoriel php
 Implémentez votre propre algorithme de hachage sha-256 en PHP !
Implémentez votre propre algorithme de hachage sha-256 en PHP !
Implémentez votre propre algorithme de hachage sha-256 en PHP !
Le hachage est également appelé « hachage ». Il reçoit tout ensemble d'informations d'entrée de n'importe quelle longueur et le transforme en une empreinte de données de longueur fixe grâce à l'algorithme de hachage. L'empreinte digitale est la valeur de hachage. Dans l’ensemble, un hachage peut être considéré comme un résumé de message.
Il existe cette fonction hash() en PHP, qui peut calculer la valeur de hachage d'une chaîne. Par curiosité, j'ai recherché sur Google les étapes spécifiques du calcul de hachage et écrit un ensemble de calculs pour la valeur de hachage sha-256 en utilisant PHP. code. Bien sûr, il existe d'autres algorithmes de hachage que sha-256, mais actuellement sha-256 est plus couramment utilisé. Voici l'algorithme de hachage actuellement publié par le National Institute of Standards and Technology :
| Algorithme de hachage | Taille d'entrée (bits) | Taille de bloc (bits) | Taille de ligne (bits) | Générer une longueur binaire (bits) | Générer une longueur hexadécimale (caractères) | |||
|---|---|---|---|---|---|---|---|---|
| sha1 | < | sha -224< 64 | 512 | 32 | 224 | |||
| sha-256 | < 64 | sha-384 | < 2^128 | |||||
| 64 | 384 | 96 | sha-512 | < | ||||
| sha- 512/224 | <2^128 | 1024 | 64 | 224 | ||||
| sha-512/256 | < | 64 | 256 | 64 | ||||
|
Pendant le processus de rédaction, j'ai principalement fait référence aux documents et sites suivants : Lane Wagner - How SHA-256 Works Step-By-Step:https://blog.boot.dev/cryptography/how-sha-2-works-step-by-step-sha-256/ Secure Hash Standard (SHS) - FIPS 180-4(官方文档):https://csrc.nist.gov/publications/detail/fips/180/4/final ASCII Table:https://www.asciitable.com/ Copier après la connexion Cet article a beaucoup de contenu et est principalement divisé en parties suivantes Lors de la lecture, les lecteurs peuvent sauter la Préparation 2 : Méthode Assistant et accéder directement à. la partie étape. Après avoir lu Lorsque vous devez utiliser la méthode spécifiée dans la partie étape, revenez en arrière et vérifiez les fonctions dans Préparation 2 : Méthode assistante.
Préparation 1 : Corps du codeNous créons un algorithme de classe pour stocker les méthodes et les attributs dont nous avons besoin pour calculer le hachage. Il n'y a qu'une seule méthode publique sha256() dans cette classe. Cette méthode transmet un paramètre de chaîne et génère la valeur de hachage sha-256 de la chaîne. Pour terminer notre calcul de hachage, nous devons suivre un total de sept étapes. Nous écrivons d'abord les appels de ces sept étapes dans le corps de la fonction sha256(). <?php
declare(strict_types=1);
class Algorithm
{
public function sha256(string $str): string
{
// 步骤一:将字符串转化为二进制
$this->step1_convert_str_to_bits($str);
// 步骤二:在最后面追加一个1
$this->step2_append_1();
// 步骤三:在数据末尾添加0,确保二进制的个数是512的倍数,最后预留64位用于存储原始长度信息
$this->step3_extend_to_multiple_of_512();
// 步骤四:把原始字符串位长度,填充到预留在最后的64位(8个字节的长整型)中
$this->step4_append_origin_length();
// 步骤五:每一个512位切分区块,在区块末尾填充0,使得每个区块位数为2048位,需要增加48行(32位一行)
$this->step5_split_blocks_and_append_48_lines();
// 步骤六:针对每一个2048位区块处理:以32位为一行,总共有64行,修改【16-63】行的数据
$this->step6_modify_blocks_appended_48_lines();
// 步骤七:压缩数据,生成最终的哈希值
return $this->step7_compress_to_final_hash();
}
}Copier après la connexion En plus de la fonction sha256(), nous avons besoin de plusieurs attributs de membre pour sauvegarder les données générées lors du processus de calcul. L'attribut $originLen est utilisé pour enregistrer la longueur d'origine de la chaîne après sa conversion en binaire. Cette valeur de longueur sera ajoutée aux données ultérieurement. L'attribut /** @var int 原始数据的二进制长度 */ private int $originLen = 0; Copier après la connexion $bits est utilisé pour stocker les données binaires obtenues après la conversion de chaîne. /** @var array 存储二进制数组 */ private array $bits; Copier après la connexion $blocks stocke les données binaires divisées en blocs. /** @var array 二进制区块 */ private array $blocks; Copier après la connexion H Les constantes requises par le hash mètre, les 8 constantes de hachage du hash-256 sont obtenues en prenant les 32 premiers chiffres de la partie décimale binaire des racines carrées des nombres premiers 2, 3, 5, 7, 11 , 13, 17 et 19. /** @var array 质数平方根常量 */
private const H = [
0x6a09e667, // 质数2的平方根取二进制小数部分前32位
0xbb67ae85, // 质数3的平方根取二进制小数部分前32位
0x3c6ef372, // 质数5的平方根取二进制小数部分前32位
0xa54ff53a, // 质数7的平方根取二进制小数部分前32位
0x510e527f, // 质数11的平方根取二进制小数部分前32位
0x9b05688c, // 质数13的平方根取二进制小数部分前32位
0x1f83d9ab, // 质数17的平方根取二进制小数部分前32位
0x5be0cd19, // 质数19的平方根取二进制小数部分前32位
];Copier après la connexion Pour les constantes ci-dessus, les étudiants intéressés peuvent également les calculer eux-mêmes. Je ne donne ici qu'un exemple de calcul simple. En prenant le nombre premier 2 comme exemple, nous obtenons d'abord sa racine carrée via la calculatrice : 1,4142135623730950488016887242097, puis prenons simplement. Partie décimale : 0.4142135623730950488016887242097, puis convertissez cette décimale décimale en binaire, le processus de conversion est le suivant : 小数转二进制
0.
0.4142135623730950488016887242097 x 2 => 0
0.8284271247461900976033774484194 x 2 => 1
0.6568542494923801952067548968388 x 2 => 1
0.3137084989847603904135097936776 x 2 => 0
0.6274169979695207808270195873552 x 2 => 1
0.2548339959390415616540391747104 x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 1
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
0.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x 2 => 0
. . .Copier après la connexion La partie décimale calculée ci-dessus en binaire, prenez les 32 premiers chiffres : 01101010 00001001 11100110 0110 0111, Convertir en représentation hexadécimale : 0x6a09e667 , le les calculs pour plusieurs autres nombres premiers sont similaires. Bien entendu, puisqu’il s’agit d’une constante, la valeur est fixe, il suffit donc de connaître son principe de calcul. Semblable à la constante de racine carrée ci-dessus, les 64 autres constantes de hash-256 sont les 32 premiers chiffres de la partie décimale binaire de chaque racine cubique des nombres premiers 2, 3, 5, ..., 311. /** @var array 质数立方根常量 */
private const K = [
0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5, 0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3, 0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc, 0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7, 0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13, 0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3, 0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5, 0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208, 0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2,
];Copier après la connexion Préparation 2 : Fonction assistantVous pouvez ignorer cette partie directement et commencer à partir de l'étape 1 ci-dessous pour calculer la valeur de hachage. Lorsque vous avez besoin d'utiliser une certaine fonction assistant, venez simplement ici pour effectuer une recherche. Dans le processus de calcul du hachage, nous stockons les données binaires dans un tableau. Chaque élément du tableau correspond à un bit binaire, donc si nous voulons effectuer AND, non-XOR et addition sur ces tableaux binaires, etc. , nous devons implémenter notre propre fonction opérationnelle. Convertissez un entier décimal en tableau binaire. /**
* 十进制整数转化为二进制数组
* @param int $num 十进制整数
* @param int $fillTo 填充到多少位,不够的用0来补齐
*/
public function int2bits(int $num, int $fillTo = 0): array
{
$bits = str_split(decbin($num));
array_walk($bits, function (&$val) {
$val = intval($val);
});
for ($len = count($bits); $len < $fillTo; $len++) {
array_unshift($bits, 0);
}
return $bits;
}Copier après la connexion Décalez un tableau binaire vers la droite du nombre de chiffres spécifié. /**
* 二进制数组向右移动
* @param array $bits 二进制数组
*/
public function rightShift(array $bits, int $move): array
{
$len = count($bits);
$move = $move % $len;
if ($move <= 0) return $bits;
return array_merge(array_fill(0, $move, 0), array_slice($bits, 0, $len-$move));
}Copier après la connexion Le tableau binaire pivote vers la droite, de la même manière que le décalage vers la droite, mais les nombres déplacés sont réinsérés dans la tête. /**
* 二进制数组向右旋转
* @param array $bits 二进制数组
*/
public function rightRotate(array $bits, int $move): array
{
$len = count($bits);
$move = $move % $len;
if ($move <= 0) return $bits;
return array_merge(array_slice($bits, $len-$move, $move), array_slice($bits, 0, $len-$move));
}Copier après la connexion Ni un tableau binaire. /**
* 二进制数组求非
* @param array $bits 二进制数组
*/
public function not(array $bits): array
{
for ($i = count($bits)-1; $i >= 0; $i--) {
$bits[$i] = ($bits[$i] == 0) ? 1 : 0;
}
return $bits;
}Copier après la connexion ET plusieurs tableaux binaires. /**
* 二进制数组求与
* @param array $args 二进制数组
*/
public function and(array ...$args): array
{
$argc = count($args);
if ($argc == 0) return [];
for ($i = 1; $i < $argc; $i++) {
$j = count($args[0]) - 1;
$k = count($args[$i]) - 1;
while ($j >= 0 || $k >= 0) {
$j < 0 and array_unshift($args[0], 0) and $j = 0; // 如果是$args[0]不够长就头插补齐
($args[$i][$k] ?? 0) == 0 and $args[0][$j] = 0;
$j--;
$k--;
}
}
return $args[0];
}Copier après la connexion XOR plusieurs tableaux binaires. /**
* 二进制数组求异或
* @param array $args 二进制数组
*/
public function xor(array ...$args): array
{
$argc = count($args);
if ($argc == 0) return [];
for ($i = 1; $i < $argc; $i++) {
$j = count($args[0]) - 1;
$k = count($args[$i]) - 1;
while ($j >= 0 || $k >= 0) {
$j < 0 and array_unshift($args[0], 0) and $j = 0; // 如果是$args[0]不够长就头插补齐
$args[0][$j] = intval($args[0][$j] != ($args[$i][$k] ?? 0));
$j--;
$k--;
}
}
return $args[0];
}Copier après la connexion Ajoutez plusieurs tableaux binaires. /**
* 二进制数组相加
* @param array $args 二进制数组
*/
public function add(array ...$args): array
{
$argc = count($args);
if ($argc == 0) return [];
for ($i = 1; $i < $argc; $i++) {
$carry = 0;
$j = count($args[0]) - 1;
$k = count($args[$i]) - 1;
while ($j >= 0 || $k >= 0) {
$j < 0 and array_unshift($args[0], 0) and $j = 0; // 如果是$args[0]不够长就头插补齐
$carry += $args[0][$j] + ($args[$i][$k] ?? 0);
switch ($carry) {
case 1: $carry = 0; $args[0][$j] = 1; break;
case 2: $carry = 1; $args[0][$j] = 0; break;
case 3: $carry = 1; $args[0][$j] = 1; break;
}
$j--;
$k--;
}
$carry == 1 and array_unshift($args[0], $carry); // 计算完后还有进位则加长存放
}
return array_slice($args[0], -32); // 计算结果只保留32位
}Copier après la connexion Imprimez un tableau binaire à des fins de débogage. Un espace sera ajouté tous les 8 bits, deux espaces seront ajoutés tous les 32 bits, une ligne sera modifiée tous les 64 bits et une ligne vide sera laissée tous les 512 bits, ce qui rend les données imprimées plus faciles à visualiser. /**
* 打印二进制数组
* @param array $bits 二进制数组
*/
public function printBits(array $bits): void
{
$len = 0;
foreach ($bits as $bit) {
if ($len > 0) {
if ($len % 512 == 0) echo PHP_EOL;
if ($len % 64 == 0) {
echo PHP_EOL;
} else {
if ($len % 32 == 0) echo ' ';
if ($len % 8 == 0) echo ' ';
}
}
echo $bit;
$len++;
}
echo PHP_EOL;
}Copier après la connexion Convertissez le tableau binaire en hexadécimal pour la dernière étape pour convertir le binaire en chaîne de valeur de hachage. /**
* 二进制数组转化为十六进制
* @param array $bits 二进制数组
*/
public function bits2hex(array $bits): string
{
$str = '';
for ($i = count($bits)-1; $i >= 0; $i -= 4) {
$dec = $bits[$i] + ($bits[$i-1] ?? 0)*2 + ($bits[$i-2] ?? 0)*4 + ($bits[$i-3] ?? 0)*8;
switch ($dec) {
case 0: $str = '0' . $str; break;
case 1: $str = '1' . $str; break;
case 2: $str = '2' . $str; break;
case 3: $str = '3' . $str; break;
case 4: $str = '4' . $str; break;
case 5: $str = '5' . $str; break;
case 6: $str = '6' . $str; break;
case 7: $str = '7' . $str; break;
case 8: $str = '8' . $str; break;
case 9: $str = '9' . $str; break;
case 10: $str = 'a' . $str; break;
case 11: $str = 'b' . $str; break;
case 12: $str = 'c' . $str; break;
case 13: $str = 'd' . $str; break;
case 14: $str = 'e' . $str; break;
case 15: $str = 'f' . $str; break;
}
}
return $str;
}Copier après la connexion Étape 1 : Convertir la chaîne en binaire Ici, nous utilisons la chaîne "hello world" pour démontrer l'ensemble du processus de calcul de hachage. Nous pouvons d'abord utiliser la fonction de hachage intégrée de PHP pour calculer le résultat. La valeur de hachage de "hello world" est "b94d27b9934d3e08a52e52d7da7dabfac484efe37a5380ee9088f7ace2efcde9". Si la valeur de hachage que nous avons finalement calculée est égale à cette valeur, notre logique de calcul est correcte. Nous divisons d'abord "hello world" en caractères. Chaque caractère a une valeur de code ASCII correspondante. Ces valeurs de code ASCII sont toutes des nombres entiers de 0 à 256. Vous pouvez utiliser la fonction ord() de PHP pour convertir ces caractères en entiers, puis convertir ces entiers en binaire correspondant et les stocker dans l'attribut $bits. Et enregistrez la valeur de longueur de $bits à ce moment-là dans l'attribut $originLen. "hello world" converti en données binaires est : “hello world” 01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 Copier après la connexion /**
* 步骤一:将字符串转化为二进制
* @param string $str 原始字符串
*/
public function step1_convert_str_to_bits(string $str): void
{
$this->bits = [];
$chars = str_split($str);
foreach ($chars as $char) {
$this->bits = array_merge($this->bits, $this->int2bits(ord($char), 8));
}
$this->originLen = count($this->bits);
}Copier après la connexion Étape 2 : ajoutez le chiffre 1 Puis ajoutez un 1 à la fin du tableau binaire. $bits 01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 1 Copier après la connexion Étape 3 : Remplissez jusqu'à des multiples de 512 在二进制数组的末尾添加 0 以使得整个二进制数组的个数刚好是 512 的倍数。需要注意的是,二进制数组的最末尾要预留 64 位用于存放原始二进制的长度。也就是一开始将字符串转换成二进制时的长度,我们在 步骤一 中将这个长度值保存到了 $originLen 属性里。 $bits 01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 [ 预留 64 位用于存储原始字符串的长度 ] Copier après la connexion /**
* 步骤三:在数据末尾添加0,确保二进制的个数是512的倍数,最后预留64位用于存储原始长度信息
*/
public function step3_extend_to_multiple_of_512(): void
{
$rem = (count($this->bits) + 64) % 512;
if ($rem > 0) {
while ($rem < 512) {
$this->bits[] = 0;
$rem++;
}
}
}Copier après la connexion 步骤四:追加原始长度信息 把之前记录的原始数据长度 $originLen 转换为 64 位的二进制追加到 $bits 末尾。 $bits 01101000 01100101 01101100 01101100 01101111 00100000 01110111 01101111 01110010 01101100 01100100 10000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000 01011000 Copier après la connexion /**
* 步骤四:把原始字符串位长度,填充到预留在最后的64位(8个字节的长整型)中
*/
public function step4_append_origin_length(): void
{
$this->bits = array_merge($this->bits, $this->int2bits($this->originLen, 64));
}Copier après la connexion 步骤五:切分区块并填充至 2048 位 经过 步骤四 之后,$bits 二进制数组的个数已经是 512 的倍数,现在以每 512 位分为一个区块,然后在每个区块末尾填充 0,让每个区块的大小变成 2048 位。每个区块的 2048 位数据以 32 位作为一行,那么就有 64 行。由于 "hello world" 数据比较短,我们就只有一个区块。
/**
* 步骤五:每一个512位切分区块,在区块末尾填充0,使得每个区块位数为2048位,经计算
* 每个区块还需要添加48x32个0
*/
public function step5_split_blocks_and_append_48_lines(): void
{
$this->blocks = [];
$append = $this->int2bits(0, 48 * 32);
$len = count($this->bits);
for ($i = 0; $i < $len; $i += 512) {
$this->blocks[] = array_merge(array_slice($this->bits, $i, 512), $append);
}
}Copier après la connexion 步骤六:区块数据修改 上一步中我们给每一个区块末尾添加了很多 0,在这一步中,通过一些位操作将这些数据进一步调整。按 32 位为一行,我们需要修改新增加的 16-63 行的数据。修改的逻辑如下: 算法逻辑 For i from w[16…63]: s0 = (w[i-15] rightrotate 7) xor (w[i-15] rightrotate 18) xor (w[i-15] rightshift 3) s1 = (w[i-2] rightrotate 17) xor (w[i- 2] rightrotate 19) xor (w[i- 2] rightshift 10) w[i] = w[i-16] + s0 + w[i-7] + s1 Copier après la connexion 其中 w 是每个区块的行数组,w[i] 就是第 i 行。 rightshift 是右移,rightrotate 是旋转右移, xor 是异或。 这里以第 16 行的处理为例: 算法详解 i = 16
(w[1] rightrotate 7) = 01101111001000000111011101101111 -> 11011110110111100100000011101110
(w[1] rightrotate 18) = 01101111001000000111011101101111 -> 00011101110110111101101111001000
(w[1] rightshift 3) = 01101111001000000111011101101111 -> 00001101111001000000111011101101
s0 = (w[1] rightrotate 7) xor (w[1] rightrotate 18) xor (w[1] rightshift 3)
= 11001110111000011001010111001011
(w[14] rightrotate 17) = 00000000000000000000000000000000 -> 00000000000000000000000000000000
(w[14] rightrotate 19) = 00000000000000000000000000000000 -> 00000000000000000000000000000000
(w[14] rightshift 10) = 00000000000000000000000000000000 -> 00000000000000000000000000000000
s1 = (w[14] rightrotate 17) xor (w[14] rightrotate 19) xor (w[14] rightshift 10)
= 00000000000000000000000000000000
w[i] = w[0] + s0 + w[9] + s1
= 00110111010001110000001000110111(相加得到的值如果超过 32 位,则抹去高位)
/**
* 步骤六:针对每一个2048位区块处理:以32位为一行,总共有64行,修改【16-63】行的数据,
* 这【16-63】行就是上一步新增的48x32个0
*/
public function step6_modify_blocks_appended_48_lines(): void
{
foreach ($this->blocks as &$block) {
for ($i = 16; $i < 64; $i++) {
$w0 = array_slice($block, ($i-16)*32, 32);
$w1 = array_slice($block, ($i-15)*32, 32);
$w9 = array_slice($block, ($i-7)*32, 32);
$w14 = array_slice($block, ($i-2)*32, 32);
$s0 = $this->xor(
$this->rightRotate($w1, 7),
$this->rightRotate($w1, 18),
$this->rightShift($w1, 3)
);
$s1 = $this->xor(
$this->rightRotate($w14, 17),
$this->rightRotate($w14, 19),
$this->rightShift($w14, 10)
);
$wi = $this->add($w0, $s0, $w9, $s1);
// 如果$wi的长度超过了32位,则只取32位,舍弃高位
$k = count($wi) - 1;
for ($j = $i * 32 + 31; $j >= $i * 32; $j--) {
$block[$j] = $wi[$k] ?? 0;
$k--;
}
}
}
}Copier après la connexion 步骤七:压缩 新建变量 $a、$b、$c、$d、$e、$f、$g、$h 值依次分别等于哈希常量 H[0-7],接着循环每一个区块的每一行,通过 与 非 异或 等操作将信息压缩到 $a、$b、$c、$d、$e、$f、$g、$h 中,最后将 $a、$b、$c、$d、$e、$f、$g、$h 的值与原始常量 H[0-7] 相加,拼接相加后的二进制结果 h0~h7 并转化为十六进制字符串得到最终的哈希值。 具体的压缩算法如下: 算法逻辑 For i from 0 to 63 s1 = (e rightrotate 6) xor (e rightrotate 11) xor (e rightrotate 25) ch = (e and f) xor ((not e) and g) temp1 = h + s1 + ch + k[i] + w[i] s0 = (a rightrotate 2) xor (a rightrotate 13) xor (a rightrotate 22) maj = (a and b) xor (a and c) xor (b and c) temp2 := s0 + maj h = g g = f f = e e = d + temp1 d = c c = b b = a a = temp1 + temp2 Copier après la connexion 这里以第 0 行的处理为例,列出了变量计算结果方便大家对照调试: 计算结果 i = 0 s1 = 00110101100001110010011100101011 ch = 00011111100001011100100110001100 temp1 = 01011011110111010101100111010100 s0 = 11001110001000001011010001111110 maj = 00111010011011111110011001100111 temp2 = 00001000100100001001101011100101 h = 00011111100000111101100110101011 g = 10011011000001010110100010001100 f = 01010001000011100101001001111111 e = 00000001001011010100111100001110 d = 00111100011011101111001101110010 c = 10111011011001111010111010000101 b = 01101010000010011110011001100111 a = 01100100011011011111010010111001 Copier après la connexion /**
* 步骤七:压缩数据
*/
public function step7_compress_to_final_hash(): string
{
$a = $h0 = $this->int2bits(static::H[0], 32);
$b = $h1 = $this->int2bits(static::H[1], 32);
$c = $h2 = $this->int2bits(static::H[2], 32);
$d = $h3 = $this->int2bits(static::H[3], 32);
$e = $h4 = $this->int2bits(static::H[4], 32);
$f = $h5 = $this->int2bits(static::H[5], 32);
$g = $h6 = $this->int2bits(static::H[6], 32);
$h = $h7 = $this->int2bits(static::H[7], 32);
foreach ($this->blocks as $block) {
for ($i = 0; $i < 64; $i++) {
$s1 = $this->xor(
$this->rightRotate($e, 6),
$this->rightRotate($e, 11),
$this->rightRotate($e, 25)
);
$ch = $this->xor(
$this->and($e, $f),
$this->and($this->not($e), $g)
);
$ki = $this->int2bits(static::K[$i], 32);
$wi = array_slice($block, $i*32, 32);
$temp1 = $this->add($h, $s1, $ch, $ki, $wi);
$s0 = $this->xor(
$this->rightRotate($a, 2),
$this->rightRotate($a, 13),
$this->rightRotate($a, 22),
);
$maj = $this->xor(
$this->and($a, $b),
$this->and($a, $c),
$this->and($b, $c)
);
$temp2 = $this->add($s0, $maj);
$h = $g;
$g = $f;
$f = $e;
$e = $this->add($d, $temp1);
$d = $c;
$c = $b;
$b = $a;
$a = $this->add($temp1, $temp2);
}
}
$h0 = $this->add($h0, $a);
$h1 = $this->add($h1, $b);
$h2 = $this->add($h2, $c);
$h3 = $this->add($h3, $d);
$h4 = $this->add($h4, $e);
$h5 = $this->add($h5, $f);
$h6 = $this->add($h6, $g);
$h7 = $this->add($h7, $h);
return $this->bits2hex(array_merge($h0, $h1, $h2, $h3, $h4, $h5, $h6, $h7));
}Copier après la connexion 至此整个哈希 sha-256 计算流程就完成了, 计算得到的哈希值也与 PHP 自带的 hash() 函数计算结果一致。 |
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
Guide d'installation et de mise à niveau de PHP 8.4 pour Ubuntu et Debian
Dec 24, 2024 pm 04:42 PM
PHP 8.4 apporte plusieurs nouvelles fonctionnalités, améliorations de sécurité et de performances avec une bonne quantité de dépréciations et de suppressions de fonctionnalités. Ce guide explique comment installer PHP 8.4 ou mettre à niveau vers PHP 8.4 sur Ubuntu, Debian ou leurs dérivés. Bien qu'il soit possible de compiler PHP à partir des sources, son installation à partir d'un référentiel APT comme expliqué ci-dessous est souvent plus rapide et plus sécurisée car ces référentiels fourniront les dernières corrections de bogues et mises à jour de sécurité à l'avenir.
 Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Date et heure de CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler avec la date et l'heure dans cakephp4, nous allons utiliser la classe FrozenTime disponible.
 Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
Discuter de CakePHP
Sep 10, 2024 pm 05:28 PM
CakePHP est un framework open source pour PHP. Il vise à faciliter grandement le développement, le déploiement et la maintenance d'applications. CakePHP est basé sur une architecture de type MVC à la fois puissante et facile à appréhender. Modèles, vues et contrôleurs gu
 Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Téléchargement de fichiers CakePHP
Sep 10, 2024 pm 05:27 PM
Pour travailler sur le téléchargement de fichiers, nous allons utiliser l'assistant de formulaire. Voici un exemple de téléchargement de fichiers.
 CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
CakePHP créant des validateurs
Sep 10, 2024 pm 05:26 PM
Le validateur peut être créé en ajoutant les deux lignes suivantes dans le contrôleur.
 Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Journalisation CakePHP
Sep 10, 2024 pm 05:26 PM
Se connecter à CakePHP est une tâche très simple. Il vous suffit d'utiliser une seule fonction. Vous pouvez enregistrer les erreurs, les exceptions, les activités des utilisateurs, les actions entreprises par les utilisateurs, pour tout processus en arrière-plan comme cronjob. La journalisation des données dans CakePHP est facile. La fonction log() est fournie
 Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Comment configurer Visual Studio Code (VS Code) pour le développement PHP
Dec 20, 2024 am 11:31 AM
Visual Studio Code, également connu sous le nom de VS Code, est un éditeur de code source gratuit – ou environnement de développement intégré (IDE) – disponible pour tous les principaux systèmes d'exploitation. Avec une large collection d'extensions pour de nombreux langages de programmation, VS Code peut être c
 Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
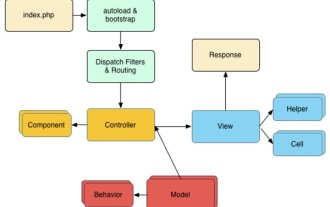
Guide rapide CakePHP
Sep 10, 2024 pm 05:27 PM
CakePHP est un framework MVC open source. Cela facilite grandement le développement, le déploiement et la maintenance des applications. CakePHP dispose d'un certain nombre de bibliothèques pour réduire la surcharge des tâches les plus courantes.





