
Cet article vous apporte des connaissances pertinentes sur Python, qui organise principalement les problématiques liées au modèle de forêt aléatoire, y compris une introduction au modèle d'ensemble, les principes de base du modèle de forêt aléatoire, l'utilisation de sklearn pour implémenter le modèle de forêt aléatoire, etc. , Jetons-y un coup d'oeil ensemble, j'espère que cela sera utile à tout le monde.

[Recommandations associées : Tutoriel vidéo Python3 ]
Le modèle d'apprentissage d'ensemble utilise une série d'apprenants faibles (également appelés modèles de base ou modèles de base) pour apprendre et combiner chacun Les résultats des apprenants faibles sont intégrés pour obtenir de meilleurs résultats d’apprentissage qu’un apprenant seul.
Les algorithmes courants pour les modèles d'apprentissage intégrés incluent l'algorithme Bagging et l'algorithme Boosting.
Le modèle d'apprentissage automatique typique de l'algorithme Bagging est le modèle de forêt aléatoire, tandis que les modèles d'apprentissage automatique typiques de l'algorithme Boosting sont les modèles AdaBoost, GBDT, XGBoost et LightGBM.
Le principe de l'algorithme de bagging est similaire au vote. Chaque apprenant faible dispose d'une voix. Enfin, sur la base des votes de tous les apprenants faibles, le résultat final de la prédiction est généré selon le principe de la « minorité ». obéit à la majorité", comme le montre la figure ci-dessous.
Supposons qu'il existe 10 000 éléments de données originales et que 10 000 données sont sélectionnées au hasard avec remplacement pour former un nouvel ensemble d'apprentissage (car elles sont échantillonnées au hasard avec remplacement, une certaine donnée peut être sélectionnée plusieurs fois , il est également possible qu'une certaine donnée n'ait pas été sélectionnée une seule fois), et qu'un apprenant faible soit formé à l'aide d'un ensemble de formation à chaque fois. De cette manière, après un échantillonnage aléatoire n fois avec remise, à la fin de la formation, n apprenants faibles formés par différents ensembles de formation peuvent être obtenus selon les résultats de prédiction de ces n apprenants faibles, conformément au principe de « l'apprentissage ». la minorité obéit à la majorité", pour obtenir un résultat de prédiction final plus précis et raisonnable.
Plus précisément, dans le problème de classification, n apprenants faibles sont utilisés pour voter pour obtenir le résultat final, et dans le problème de régression, la moyenne de n apprenants faibles est prise comme résultat final.
L'essence de l'algorithme de boosting est d'améliorer les apprenants faibles en apprenants forts. La différence entre celui-ci et l'algorithme de bagging est que l'algorithme de bagging traite tous les apprenants faibles de la même manière, tandis que l'algorithme de boosting traite les apprenants faibles de la même manière. En termes simples, le traitement signifie se concentrer sur « la culture des élites » et « prêter attention aux erreurs ».
« Culture des élites » signifie qu'après chaque cycle de formation, les apprenants faibles avec des résultats de prédiction plus précis reçoivent un poids plus élevé, et les apprenants faibles avec des performances médiocres reçoivent des poids inférieurs. De cette façon, dans la prédiction finale, le « modèle excellent » a un poids important, ce qui équivaut à sa capacité à émettre plusieurs votes, tandis que le « modèle général » ne peut émettre qu'un seul vote ou ne peut pas voter.
« Faites attention aux erreurs » signifie modifier le poids ou la distribution de probabilité de l'ensemble d'entraînement après chaque cycle d'entraînement, en augmentant le poids des exemples qui ont été mal prédits par l'apprenant faible au cycle précédent, et en réduisant le poids. des exemples qui ont été mal appris par l'apprenant faible lors du tour précédent. Le poidsde l'exemple correct prédit par la machine est utilisé pour accroître l'accent mis par l'apprenant faible sur les données qui prédisent incorrectement, améliorant ainsi l'effet de prédiction global. du modèle. 2 Principes de base du modèle de forêt aléatoire
Random Forest (Random Forest) est un modèle d'ensachage classique, et son apprenant faible est un modèle d'arbre de décision.Comme le montre la figure ci-dessous, le modèle de forêt aléatoire échantillonnera de manière aléatoire à partir de l'ensemble de données d'origine pour former n différents ensembles de données échantillons, puis construira n modèles d'arbre de décision différents basés sur ces ensembles de données, et enfin sur la base de la moyenne de ceux-ci. modèles d'arbre de décision (pour les modèles de régression) ou vote (pour les modèles de classification) pour obtenir les résultats finaux.
Afin de garantir la capacité de généralisation (ou capacité universelle) du modèle, le modèle de forêt aléatoire suit souvent les deux principes de base des « données aléatoires » et des « caractéristiques aléatoires » lors de la construction de chaque arbre.
Données aléatoires: extrayez aléatoirement les données de toutes les données avec remplacement comme données de formation pour l'un des modèles d'arbre de décision. Par exemple, il existe 1 000 données originales, extraites 1 000 fois avec remplacement, pour former un nouvel ensemble de données permettant de former un certain modèle d’arbre de décision.
Fonctionnalité aléatoire: si la dimension de la caractéristique de chaque échantillon est M, spécifiez une constante k
Comparé à un modèle d'arbre de décision unique, le modèle de forêt aléatoire intègre plusieurs arbres de décision, de sorte que ses résultats de prédiction seront plus précis, il ne provoquera pas facilement un surajustement et sa capacité de généralisation sera plus forte.
Le modèle de forêt aléatoire peut effectuer à la fois une analyse de classification et une analyse de régression. Les modèles correspondants sont :
· Modèle de classification de forêt aléatoire (RandomForestClassifier)
· Forêt aléatoire. Modèle de régression (RandomForestRegressor)
L'apprenant faible du modèle de classification forestière aléatoire est le modèle d'arbre de décision de classification, et l'apprenant faible du modèle de régression forestière aléatoire est le modèle d'arbre de décision de régression.
Le code est le suivant.
from sklearn.ensemble import RandomForestClassifier X = [[1,2],[3,4],[5,6],[7,8],[9,10]] y = [0,0,0,1,1] # 设置弱学习器数量为10 model = RandomForestClassifier(n_estimators=10,random_state=123) model.fit(X,y) model.predict([[5,5]]) # 输出为:array([0])
Cette section explique comment utiliser les données de base des actions pour obtenir certaines données de variables dérivées, telles que le prix moyen mobile sur 5 jours MA5 et 10, indicateurs de moyenne mobile couramment utilisés dans l'analyse technique des actions. Prix moyen mobile quotidien MA10, indicateur de force relative RSI, indicateur de dynamique MOM, moyenne mobile exponentielle EMA, convergence et divergence moyenne mobile MACD, etc.
Utilisez d'abord la fonction get_k_data() pour obtenir les données boursières de base du 01/01/2015 au 31/12/2019.
Les 5 premières lignes de données sont présentées dans la figure ci-dessous, et les données manquantes sont des données de jours fériés (jours non commerciaux).
Utilisez la fonction set_index() pour définir la colonne de date sur l'index de ligne, le code est le suivant.
Certaines données de variables dérivées simples peuvent être générées via le code suivant.
moyen de clôture-ouverture (cours de clôture - cours d'ouverture)/cours d'ouverture
moyen haut-bas (prix le plus élevé - prix le plus bas)/prix le plus bas
pre_close signifie cours de clôture d'hier, utilisez shift ; (1) Déplacez toutes les données de la colonne de fermeture vers le bas d'une ligne et formez une nouvelle colonne. S'il s'agit d'un décalage (-1), cela signifie monter d'une ligne
price_change signifie le cours de clôture d'aujourd'hui - le cours de clôture d'hier, c'est-à-dire ; c'est-à-dire ce jour-là La variation du cours de l'action
p_change représente la variation en pourcentage du cours de l'action ce jour-là, également connue sous le nom d'augmentation ou de diminution du cours de l'action ce jour-là.
La moyenne mobile sur 5 jours et la moyenne mobile sur 10 jours du cours de l'action peuvent être générées via le code suivant.
Remarque : L'utilisation de la fonction glissante
Parmi eux, MA signifie moyenne mobile, « moyenne » fait référence à la moyenne arithmétique de la clôture des n derniers jours et « mobile » fait référence à toujours dans le calcul utilise les données de prix des n derniers jours.
Par exemple : calcul MA5
Selon les données ci-dessus, la valeur MA5 du n°5 est (1,2+1,4+1,6+1,8+2,0)/5=1,6, tandis que la valeur MA5 du n°5 est (1,2+1,4+1,6+1,8+2,0)/5=1,6. 6 vaut (1,4 +1,6+1,8+2,0+2,2)/5=1,8, et ainsi de suite. La moyenne mobile des cours des actions sur une période donnée est reliée à une courbe, qui est la moyenne mobile. De même, MA10 est le cours moyen de l’action des 10 jours précédents à compter du jour du calcul.
Lors du calcul de données comme MA5, parce que la quantité de données dans les 4 premiers jours n'est pas suffisante, la moyenne mobile correspondant à ces 4 jours ne peut pas être calculée, donc une valeur nulle NaN sera générée. Habituellement, la fonction dropna() est utilisée pour supprimer les valeurs nulles afin d'éviter les problèmes causés par les valeurs nulles dans les calculs ultérieurs. Le code est le suivant.
Vous pouvez constater que les lignes avant le 16 ont été supprimées.
La valeur RSI de l'indice de force relative peut être générée via le code suivant.
La valeur RSI peut refléter la force de la hausse du cours de l'action par rapport à la baisse à court terme, nous aidant à mieux juger de la tendance à la hausse et à la baisse du cours de l'action.
Plus la valeur RSI est élevée, plus la tendance à la hausse est forte par rapport à la tendance à la baisse, et inversement, plus la tendance à la hausse est faible par rapport à la tendance à la baisse.
La formule de calcul de la valeur RSI est la suivante.
Exemple :
D'après les données du tableau ci-dessus, en prenant N=6, le prix moyen en hausse en 6 jours peut être obtenu comme (2+2+2)/6=1, et le le prix moyen en baisse sur 6 jours est (1+1+1 )/6=0,5, donc la valeur RSI est (1/(1+0,5))×100=66,7.
Normalement, la valeur RSI est comprise entre 20 et 80. Si elle dépasse 80, elle est surachetée, si elle est inférieure à 20, elle est survendue. Si elle est égale à 50, on considère que le pouvoir des acheteurs et des vendeurs. est égal. Par exemple, si le cours de l'action augmente pendant 6 jours consécutifs, la baisse moyenne du cours le 6ème jour sera de 0 et la valeur RSI du 6ème jour sera de 100. Cela indique que l'acheteur d'actions est dans une position très forte à cette fois, mais il est également rappelé aux investisseurs de se méfier du fait que cela peut aussi être une période excessive. Dans l'état d'achat, il faut prévenir le risque de baisse du cours des actions.
Vous pouvez générer la valeur MOM de l'indicateur d'élan via le code suivant.
MOM est l'abréviation de momentum, qui reflète le taux de hausse et de baisse des cours des actions sur une période de temps La formule de calcul est la suivante.
Exemple :
Supposons que vous souhaitiez calculer la valeur MOM du n° 6 et que le paramètre timeperiod soit défini sur 5 dans le code précédent, vous devez alors soustraire le prix de clôture de N° 1 à partir du cours de clôture du prix n° 6, c'est-à-dire que la valeur MOM du n° 6 est de 2,2-1,2=1 De même, la valeur MOM du n° 7 est de 2,4-1,4=1. La connexion des valeurs MOM pour des jours consécutifs forme une courbe qui reflète la hausse et la baisse du cours de l'action.
Vous pouvez générer une moyenne mobile exponentielle EMA via le code suivant.
EMA est une moyenne mobile pondérée décroissante de façon exponentielle et est analysée en fonction des résultats du calcul. Elle est utilisée pour déterminer la tendance des tendances futures du cours des actions.
La formule de calcul de l'EMA est la suivante.
Parmi eux, EMAtoday est la valeur EMA du jour ; Pricetoday est le cours de clôture du jour ; EMAyesterday est la valeur EMA d'hier α est l'indice de lissage, généralement la valeur est 2/(N+1), N représente le nombre de jours, lorsque N est 6, α est 2/7 et l'EMA correspondante est appelée EMA6, qui est la moyenne mobile exponentielle sur 6 jours. La formule continue de se répéter jusqu'à ce que la première valeur EMA apparaisse (la première valeur EMA est généralement la moyenne des cinq premiers nombres).
Exemple : EMA6
La première valeur EMA est la moyenne des 5 premiers nombres, il n'y a donc pas de valeur EMA dans les 5 premiers jours ; est les 5 premiers jours La valeur moyenne est 1 ; la valeur EMA du n° 7 est la deuxième valeur EMA. Le processus de calcul est le suivant.
Vous pouvez générer les valeurs MACD de convergence et de divergence de moyenne mobile via le code suivant.
MACD est un indicateur couramment utilisé en bourse. Il s'agit d'une variable dérivée basée sur la valeur EMA. La méthode de calcul est relativement compliquée. Les lecteurs intéressés peuvent se renseigner par eux-mêmes. Ici, il vous suffit de savoir que le MACD est un indicateur de tendance et que ses changements représentent les changements dans les tendances du marché à différents niveaux de la ligne K et représentent la tendance d'achat et de vente dans le cycle de niveaux actuel. 首先强调最核心的一点:应该是用当天的股价数据预测下一天的股价涨跌情况,所以目标变量y应该是下一天的股价涨跌情况。为什么是用当天的股价数据预测下一天的股价涨跌情况呢?这是因为特征变量中的很多数据只有在当天交易结束后才能确定(例如,收盘价close只有收盘了才有),所以当天正在交易时的股价涨跌情况是无法预测的,而等到收盘时尽管所需数据齐备,但是当天的股价涨跌情况已成定局,也就没有必要预测了,所以是用当天的股价数据预测下一天的股价涨跌情况。 第2行代码中使用了NumPy库中的where()函数,传入的3个参数的含义分别为判断条件、满足条件的赋值、不满足条件的赋值。其中df['price_change'].shift(-1)是利用shift()函数将price_change(股价变化)这一列的所有数据向上移动1行,这样就获得了每一行对应的下一天的股价变化。因此,这里的判断条件就是下一天的股价变化是否大于0,如果大于0,说明下一天股价涨了,则y赋值为1;如果不大于0,说明下一天股价不变或跌了,则y赋值为-1。预测结果就只有1或-1两种分类。 这里需要注意的是,划分要按照时间序列进行,而不能用train_test_split()函数进行随机划分。这是因为股价的变化趋势具有时间性特征,而随机划分会破坏这种特征,所以需要根据当天的股价数据预测下一天的股价涨跌情况,而不能根据任意一天的股价数据预测下一天的股价涨跌情况。 将前90%的数据作为训练集,后10%的数据作为测试集,代码如下。 设置模型参数:决策树的最大深度max_depth设置为3,即每个决策树最多只有3层;弱学习器(即决策树模型)的个数n_estimators设置为10,即该随机森林中共有10个决策树;叶子节点的最小样本数min_samples_leaf设置为10,即如果叶子节点的样本数小于10则停止分裂;随机状态参数random_state的作用是使每次运行结果保持一致,这里设置的数字123没有特殊含义,可以换成其他数字。 用predict_proba()函数可以预测属于各个分类的概率,代码如下。 通过如下代码可以查看整体的预测准确度。 打印输出score为0.40,说明模型对整个测试集中约40%的数据预测正确。这一预测准确度并不算高,也的确符合股票市场千变万化的特点。 通过如下代码可以分析各个特征变量的特征重要性。 由图可知,当日收盘价close、MA5、MACDhist相关指标等特征变量对下一天股价涨跌结果的预测准确度影响较大。 前面已经评估了模型的预测准确度,不过在商业实战中,更关心它的收益回测曲线(又称为净值曲线),也就是看根据搭建的模型获得的结果是否比不利用模型获得的结果更好。 可视化结果如下图所示。图中上方的曲线为根据模型得到的收益率曲线,下方的曲线为股票本身的收益率曲线,可以看到,利用模型得到的收益还是不错的。 要说明的是,这里讲解的量化金融内容比较浅显,搭建的模型过于理想化,真正的股市是错综复杂的,股票交易也有很多限制,如不能做空、不能T+0交易,还要考虑手续费等因素。 随机森林模型是一种非常重要的集成模型,它集成了决策树模型的众多优点,又规避了决策树模型容易过度拟合等缺点,在实战中应用较为广泛。 【相关推荐:Python3视频教程 】4.2 模型搭建
4.2.1 引入需要搭建的库
# 导入相关库
import tushare as ts
import numpy as np
import pandas as pd
import talib
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score
4.2.2 获取数据
# 1.股票基本数据获取
import tushare as ts
df = ts.get_k_data('000002',start='2015-01-01',end='2019-12-31')
df = df.set_index('date')
# 2.简单衍生变量数据构造
df['close-open'] = (df['close'] - df['open']) / df['open']
df['high-low'] = (df['high'] - df['low']) / df['low']
df['pre_close'] = df['close'].shift(1)
df['price_change'] = df['close'] - df['pre_close']
df['p_change'] = (df['close'] - df['pre_close']) / df['pre_close'] * 100
# 3.移动平均线相关数据构造
df['MA5'] = df['close'].rolling(5).mean()
df['MA10'] = df['close'].rolling(10).mean()
df.dropna(inplace=True)
# 4.通过TA-Lib库构造衍生变量数据
df['RSI'] = talib.RSI(df['close'],timeperiod=12)
df['MOM'] = talib.MOM(df['close'],timeperiod=5)
df['EMA12'] = talib.EMA(df['close'],timeperiod=12) #12日指移动平均值数
df['EMA26'] = talib.EMA(df['close'],timeperiod=26) #26日指移动平均值数
df['MACD'],df['MACDsignal'],df['MACDhist'] = talib.MACD(df['close'],fastperiod=6,slowperiod=12,signalperiod=9)
df.dropna(inplace=True)4.2.3 提取特征变量和目标变量
X = df[['close','volume','close-open','MA5','MA10','high-low','RSI','MOM','EMA12','MACD','MACDsignal','MACDhist']]
y = np.where(df['price_change'].shift(-1) > 0,1,-1)
4.2.4 划分训练集和测试集
X_length = X.shape[0]
split = int(X_length * 0.9)
X_train,X_test = X[:split],X[split:]
y_train,y_test = y[:split],y[split:]
4.2.5 模型搭建
model = RandomForestClassifier(max_depth=3,n_estimators=10,min_samples_leaf=10,random_state=123)
model.fit(X_train,y_train)
4.3 模型评估与使用
4.3.1 预测下一天的股价涨跌情况
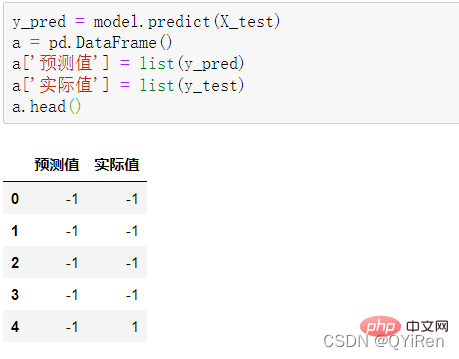
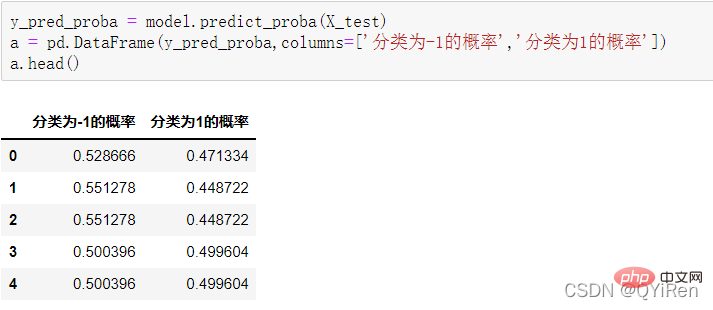
4.3.2 模型准确度评估
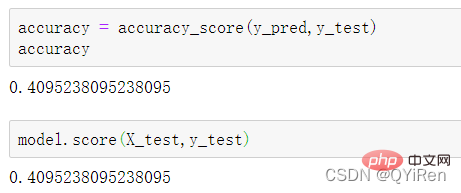
4.3.3 分析特征变量的特征重要性
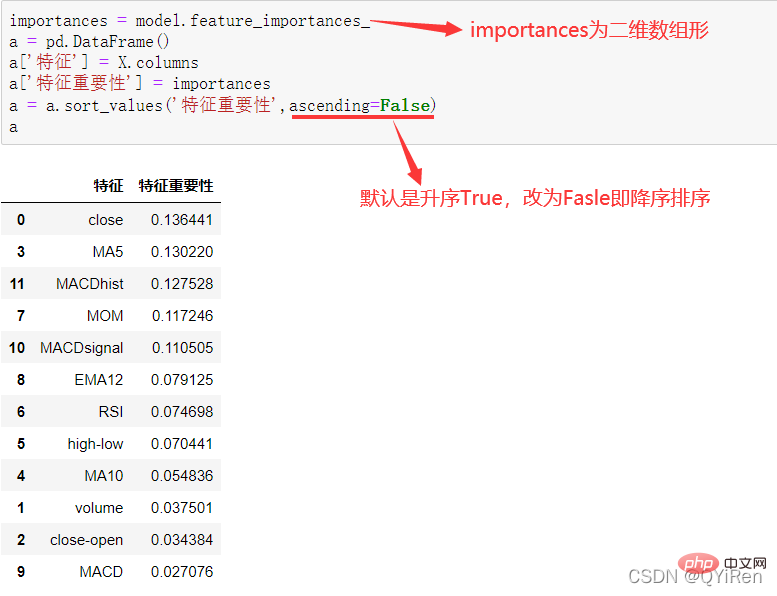
4.4 参数调优
from sklearn.model_selection import GridSearchCV
parameters={'n_estimators':[5,10,20],'max_depth':[2,3,4,5,6],'min_samples_leaf':[5,10,20,30]}
new_model = RandomForestClassifier(random_state=123)
grid_search = GridSearchCV(new_model,parameters,cv=6,scoring='accuracy')
grid_search.fit(X_train,y_train)
grid_search.best_params_
# 输出
# {'max_depth': 5, 'min_samples_leaf': 20, 'n_estimators': 5} 4.5 收益回测曲线绘制
# 在测试数据上添加一列,预测收益
X_test['prediction'] = model.predict(X_test)
# 计算每天的股价变化率
X_test['p_change'] = (X_test['close'] - X_test['close'].shift(1)) / X_test['close'].shift(1)
# 计算累积收益率
# 例如,初始股价是1,2天内的价格变化率为10%
# 那么用cumprod()函数可以求得2天后的股价为1×(1+10%)×(1+10%)=1.21
# 此结果也表明2天的收益率为21%。
X_test['origin'] = (X_test['p_change'] + 1).cumprod()
# 计算利用模型预测后的收益率
X_test['strategy'] = (X_test['prediction'].shift(1) * X_test['p_change'] + 1).cumprod()
X_test[['strategy','origin']].dropna().plot()
# 设置自动倾斜
plt.gcf().autofmt_xdate()
plt.show()
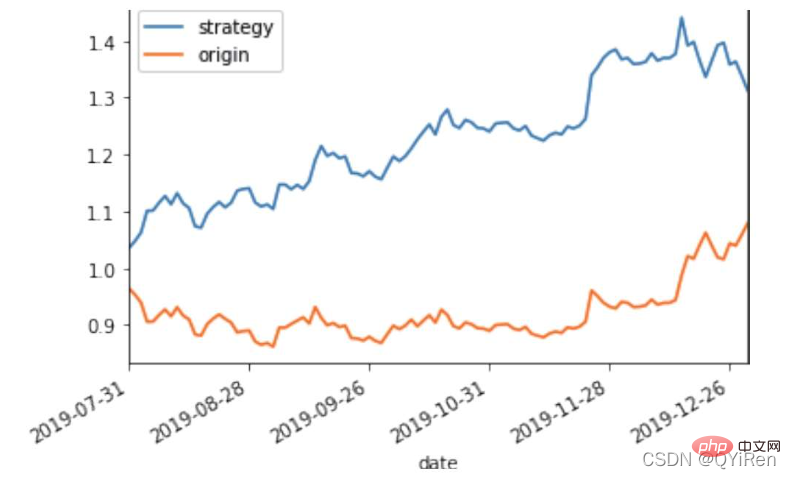
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!