Parlons de la façon d'utiliser le bruit Perlin pour dessiner des graphiques sympas en CSS !

Qu'est-ce que le bruit blanc ? Comment utiliser le bruit Perlin pour dessiner des graphiques sympas en CSS ? L'article suivant vous expliquera comment utiliser le bruit pour créer de superbes graphiques CSS. J'espère qu'il vous sera utile !

En temps normal, j'aime utiliser CSS pour créer des graphiques intéressants. [Apprentissage recommandé : Tutoriel vidéo CSS]

Regardons d'abord un exemple simple. Tout d'abord, supposons que nous implémentions une grille 10x10 :

À ce stade, nous pouvons utiliser des effets aléatoires pour optimiser ce modèle. Par exemple, nous y ajoutons différentes couleurs au hasard :

Bien que le hasard soit utilisé pour remplir aléatoirement la couleur de chaque grille, ce qui semble un peu intéressant, mais ce n'est qu'un graphique désordonné, et il n'y a aucune sensation artistique. .

Pourquoi est-ce ? Parce que le caractère aléatoire ici est complètement aléatoire et constitue une sorte de bruit blanc.

Qu'est-ce que le bruit blanc ?

Noise est en fait un générateur de nombres aléatoires.

Alors, qu'est-ce que le bruit blanc ? Si vous le comprenez du point de vue d'un programmeur, vous pouvez comprendre que la fonction random() que nous utilisons en JavaScript, le nombre généré est à peu près complètement aléatoire dans la plage de 0 à 1.

La base du bruit est constituée de nombres aléatoires. Par exemple, si nous ajoutons une couleur aléatoire à chaque grille des graphiques ci-dessus, nous obtenons un bloc graphique désordonné et sans grande beauté.

Le bruit blanc ou bruit blanc est un signal aléatoire dont la puissance densité spectrale est constante. En d’autres termes, la densité spectrale de puissance de ce signal est la même dans chaque bande de fréquence. Puisque la lumière blanche est mélangée à de la lumière monochromatique de différentes fréquences (couleurs), ce signal a la propriété d’avoir un spectre de puissance plat. "blanc", ce signal est aussi appelé bruit blanc.

Parce que les graphiques générés par l'utilisation du bruit blanc ne semblent pas naturels et peu esthétiques.

Observez les bruits naturels dans la vraie vie, ils ne ressemblent pas à ceux ci-dessus. Par exemple, la texture du bois et les ondulations des montagnes ont tendance à avoir une forme fractale, c'est-à-dire qu'elles contiennent différents niveaux de détails. Ces composants aléatoires ne sont pas complètement indépendants et il existe une certaine corrélation entre eux. Et apparemment, le bruit blanc ne fait pas ça.

Perlin Noise

De cette façon, nous introduisons naturellement Perlin Noise.

Le bruit Perlin (Perlin noise) fait référence à l'algorithme de génération de bruit naturel inventé par Ken Perlin.

Avant de l'introduire, jetons un coup d'œil au graphique ci-dessus. À quoi cela ressemblerait-il si nous n'utilisions pas de bruit blanc (complètement aléatoire), mais du bruit Perlin ?

Cela peut ressembler à ceci :

Ici, j'ai fait une animation. Vous pouvez sentir que chaque clic est le résultat de l'utilisation de la randomisation du bruit Perlin pour donner à chaque grille une couleur aléatoire différente :

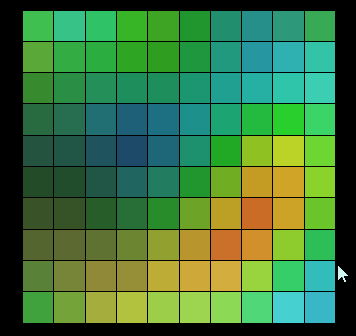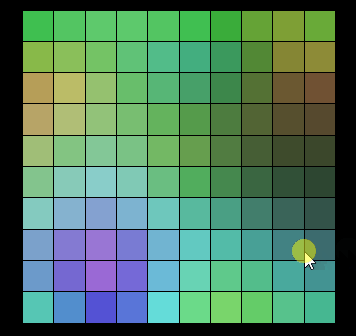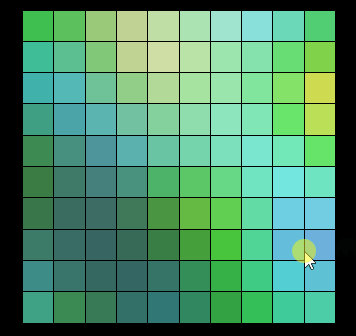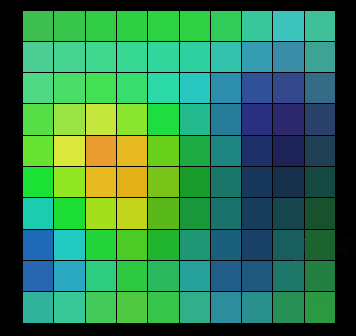
Vous pouvez voir. que les graphiques générés par l'effet aléatoire de Perlin Noise ne sont pas sans rapport les uns avec les autres. Les changements entre eux sont continus et il n'y a pas de saut entre eux. Cet effet aléatoire est similaire aux effets aléatoires de la nature, tels que les changements dans la texture du bois et les chaînes de montagnes mentionnés ci-dessus.

Comme mentionné ci-dessus, le bruit est en fait un générateur de nombres aléatoires. Et ici :

• Le problème avec le bruit blanc est qu'il est trop aléatoire et n'a aucune règle du tout

• Et Le bruit Perlin est basé sur le hasard et utilise des courbes d'assouplissement pour effectuer une interpolation douce sur ce base , rendant l'effet de bruit final plus naturel

La méthode d'implémentation spécifique est iciImplémentation améliorée de la référence Noise, vous pouvez y jeter un oeil, il n'y a en fait pas beaucoup de code source :

// This code implements the algorithm I describe in a corresponding SIGGRAPH 2002 paper.
// JAVA REFERENCE IMPLEMENTATION OF IMPROVED NOISE - COPYRIGHT 2002 KEN PERLIN.

public final class ImprovedNoise {
   static public double noise(double x, double y, double z) {
      int X = (int)Math.floor(x) & 255,                  // FIND UNIT CUBE THAT
          Y = (int)Math.floor(y) & 255,                  // CONTAINS POINT.
          Z = (int)Math.floor(z) & 255;
      x -= Math.floor(x);                                // FIND RELATIVE X,Y,Z
      y -= Math.floor(y);                                // OF POINT IN CUBE.
      z -= Math.floor(z);
      double u = fade(x),                                // COMPUTE FADE CURVES
             v = fade(y),                                // FOR EACH OF X,Y,Z.
             w = fade(z);
      int A = p[X  ]+Y, AA = p[A]+Z, AB = p[A+1]+Z,      // HASH COORDINATES OF
          B = p[X+1]+Y, BA = p[B]+Z, BB = p[B+1]+Z;      // THE 8 CUBE CORNERS,

      return lerp(w, lerp(v, lerp(u, grad(p[AA  ], x  , y  , z   ),  // AND ADD
                                     grad(p[BA  ], x-1, y  , z   )), // BLENDED
                             lerp(u, grad(p[AB  ], x  , y-1, z   ),  // RESULTS
                                     grad(p[BB  ], x-1, y-1, z   ))),// FROM  8
                     lerp(v, lerp(u, grad(p[AA+1], x  , y  , z-1 ),  // CORNERS
                                     grad(p[BA+1], x-1, y  , z-1 )), // OF CUBE
                             lerp(u, grad(p[AB+1], x  , y-1, z-1 ),
                                     grad(p[BB+1], x-1, y-1, z-1 ))));
   }
   static double fade(double t) { return t * t * t * (t * (t * 6 - 15) + 10); }
   static double lerp(double t, double a, double b) { return a + t * (b - a); }
   static double grad(int hash, double x, double y, double z) {
      int h = hash & 15;                      // CONVERT LO 4 BITS OF HASH CODE
      double u = h<8 ? x : y,                 // INTO 12 GRADIENT DIRECTIONS.
             v = h<4 ? y : h==12||h==14 ? x : z;
      return ((h&1) == 0 ? u : -u) + ((h&2) == 0 ? v : -v);
   }
   static final int p[] = new int[512], permutation[] = { 151,160,137,91,90,15,
   131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
   190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
   88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
   77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
   102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
   135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
   5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
   223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
   129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
   251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
   49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
   138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
   };
   static { for (int i=0; i < 256 ; i++) p[256+i] = p[i] = permutation[i]; }
}

Bien sûr, cet article ne concerne pas spécifiquement le bruit de Berlin Comment l'implémenter Quiconque lit le code ci-dessus sera confus. Il faut juste savoir que l'on peut utiliser le bruit Perlin pour construire des effets graphiques plus réguliers. Rendre nos graphismes plus beaux.

Utilisez CSS-doodle pour utiliser le bruit Perlin en CSS

Alors, comment utilisons-nous le

bruit Perlin en CSS ?

一种方式是找一些现成的库，譬如 p5.js 里面的 noise 函数。

当然，这里，我习惯使用 CSS-doodle，这个 CSS 图形构建库我在多篇文章中已经都有介绍过。

简单而言，CSS-doodle 它是一个基于 Web-Component 的库。允许我们快速的创建基于 CSS Grid 布局的页面，并且提供各种便捷的指令及函数（随机、循环等等），让我们能通过一套规则，得到不同 CSS 效果。可以简单看看它的主页 -- Home Page of CSS-doodle，只需要 5min 也许就能快速上手。

譬如上述的图形，它的全部代码：

<css-doodle grid="10x10">
    :doodle {
        @size: 50vmin;
        gap: 1px;
    }
   
    background: hsl(@rn(255, 1, 2), @rn(10%, 90%), @rn(10%, 90%));
</css-doodle>

没错，只需要这么寥寥几句，就可以勾勒出这样一幅图案：

CSS Pattern -- CSS Doodle

https://codepen.io/Chokcoco/pen/eYMNWNq

简单解释下：

• css-doodle 是基于 Web-Component 封装的，基本所有的代码都写在 <css-doodle> 标签内，当然也可以写一些原生 CSS/JavaScript 辅助

• 使用 grid="10x10" 即可生成一个 10x10 的 Grid 网格，再配合 @size: 50vmin，表示生成一个宽高大小为 50vmin 的 10x10 Grid 网格布局，其中 gap: 1px 表示 Gird 网格布局的 gap

• 最后，整个代码的核心部分即是 background: hsl(@rn(255, 1, 2), @rn(10%, 90%), @rn(10%, 90%))，这里即表示对每个 grid item 赋予背景色，其中 @rn()，就是最核心的部分，利用了柏林噪声算法，有规律的将背景色 map 到每一个 grid 上

当然，最新的 CSS-doodle 文档上暂时还查不到 @rn() function 的用法。为此我特意请教了下该库的作者袁川老师。

得到的回复是，官网近期会重构，所以目前没有更新最新的语法。同时，@rn() 的实现使用的就是柏林噪声的实现。同时，函数相当于是类似 p5.js 里面的 noise 函数同时做了 map，map 到前面函数参数设定的 from 到 to 范围内。

这里的 @rn() 柏林噪声随机会根据 Grid 网格，Map 到每一个网格上，使之相邻的 Grid item 之间的值，存在一定的关联。

举个栗子，我们有个 10x10 的 Grid 布局，给其每个 Grid item，添加一个伪元素，伪元素的内容，使用 @r(100) 进行填充，注意，@r() 函数是没有规律的完全随机，那么生成的数字大概是这样的：

可以看到，它们每个各自之间的数字，是完全随机毫无关联的。

如果我们使用有关联的柏林噪声随机呢？使用 @rn(100) 填充每个格子的话，大概是这样：

观察一下，很容易发现，相邻的盒子之间，或者多个连续的格子之间，存在一定的关联性，这就使得，我们利用它创造出来的图形，会具备一定的规律。

可以简单看看源码的实现，当前，前提是你需要对 CSS-doodle 的用法有一定的了解：

    rn({ x, y, context, position, grid, extra, shuffle }) {
      let counter = 'noise-2d' + position;
      let [ni, nx, ny, nm, NX, NY] = last(extra) || [];
      let isSeqContext = (ni && nm);
      return (...args) => {
        let {from = 0, to = from, frequency = 1, amplitude = 1} = get_named_arguments(args, [
          'from', 'to', 'frequency', 'amplitude'
        ]);

        if (args.length == 1) {
          [from, to] = [0, from];
        }
        if (!context[counter]) {
          context[counter] = new Perlin(shuffle);
        }
        frequency = clamp(frequency, 0, Infinity);
        amplitude = clamp(amplitude, 0, Infinity);
        let transform = [from, to].every(is_letter) ? by_charcode : by_unit;
        let t = isSeqContext
          ? context[counter].noise((nx - 1)/NX * frequency, (ny - 1)/NY * frequency, 0)
          : context[counter].noise((x - 1)/grid.x * frequency, (y - 1)/grid.y * frequency, 0);
        let fn = transform((from, to) => map2d(t * amplitude, from, to, amplitude));
        let value = fn(from, to);
        return push_stack(context, 'last_rand', value);
      };
    },

语法大概是 @rn(from, to, frequency, amplitude)，其中 from、to 表示随机范围，而 frequency 表示噪声的频率，amplitude 表示噪声的振幅。这两个参数可以理解为控制随机效果的频率和幅度。

其中 new Perlin(shuffle) 即运用到了柏林噪声算法。

Show Time

OK，上文介绍了很多与噪声和 CSS-doodle 相关的知识，下面我们回归 CSS，回归本文的主体。

在上述图形的基础上，我们可以再添加上随机的 scale()、以及 skew()。如果是完全随机的话，代码是这样的：

<css-doodle grid="20">
    :doodle {
        grid-gap: 1px;
        width: 600px; height: 600px;
    }
    background: hsl(@r(360), 80%, 80%);
    transform: 
        scale(@r(1.1, .3, 3)) 
        skew(@r(-45deg, 45deg, 3));
</css-doodle>

html,
body {
    width: 100%;
    height: 100%;
    background-color: #000;
}

上述代码表示的是一个 20x20 的 Grid 网格，每个 Grid item 都设置了完全随机的背景色、scale() 以及 skew()。当然，这里我们用的是 @r()而不是 @rn()，每个格子的每个属性的随机，没有任何的关联，那么我们会得到这样一幅图案：

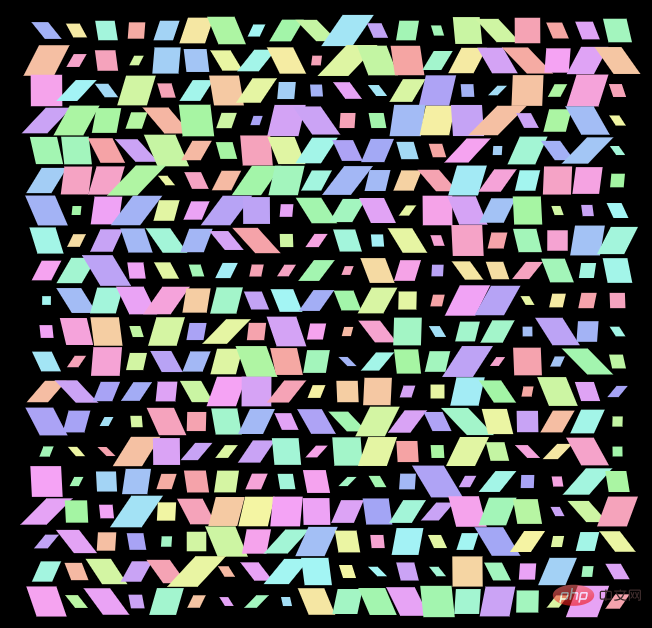
好吧，这是什么鬼，毫无美感可言。我们只需要在上述代码的基础上，将普通的完全随机，改为柏林噪声随机 @rn()：

<css-doodle grid="20">
    :doodle {
        grid-gap: 1px;
        width: 600px; height: 600px;
    }
    background: hsl(@rn(360), 80%, 80%);
    transform: 
        scale(@rn(1.1, .3, 3)) 
        skew(@rn(-45deg, 45deg, 3));
</css-doodle>

此时，就能得到完全不一样的效果：

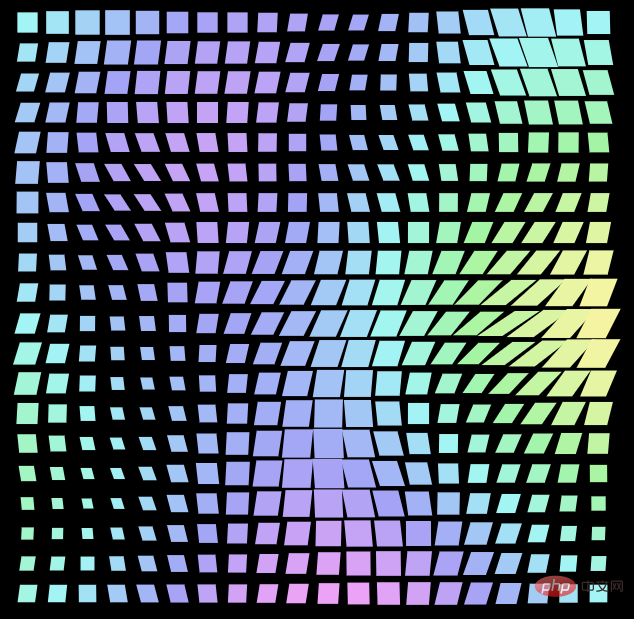
这是由于，每个 Grid item 的随机效果，都基于它们在 Grid 布局中的位置，彼此存在关联，这就是柏林噪声随机的效果。

我可以再添加上 hue-rotate 动画：

html,
body {
    width: 100%;
    height: 100%;
    background-color: #000;
    animation: change 10s linear infinite;
}
@keyframes change {
    10% {
        filter: hue-rotate(360deg);
    }
}

看看效果，并且，在 CSS-doodle 中，由于随机效果，每次刷新，都可以得到不一样的图案：

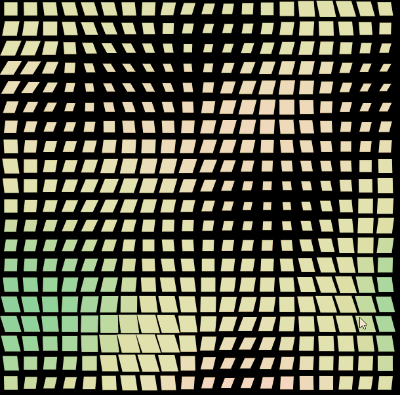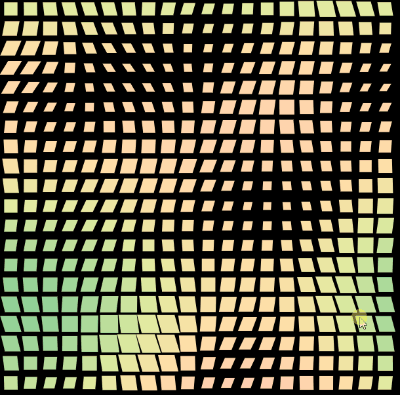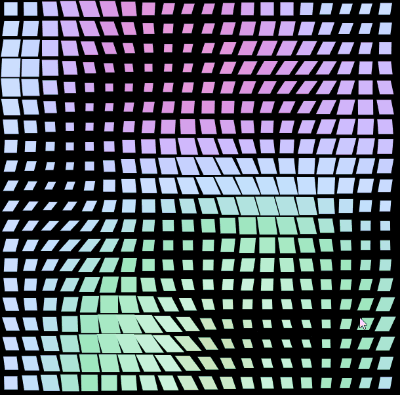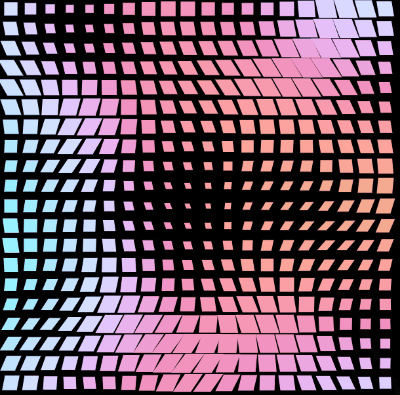
CSS Doodle - CSS Pattern2

https://codepen.io/Chokcoco/pen/mdxJrGR

当然，这个样式还可以搭配各式各样其他的 idea，像是这样：

CSS Doodle - CSS Pattern 3

https://codepen.io/Chokcoco/pen/wvmazOy

又或者是这样：

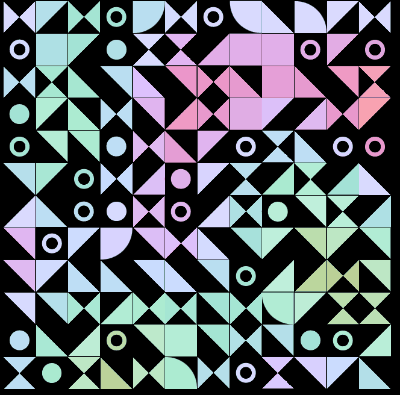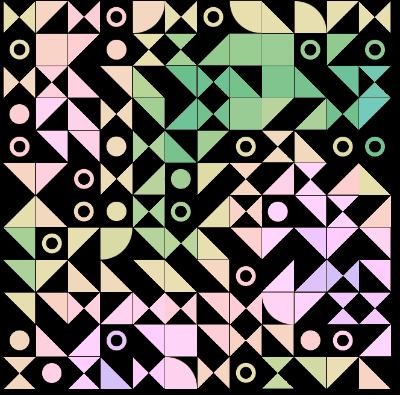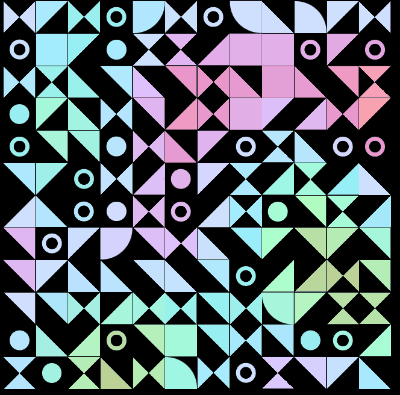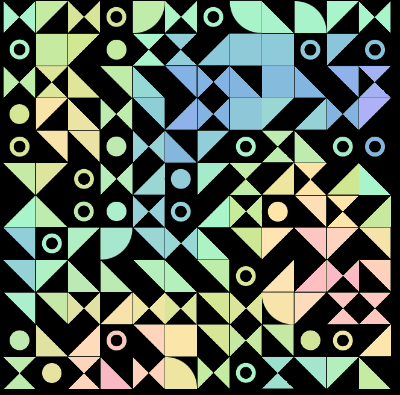
CSS Doodle - CSS Pattern 4

https://codepen.io/Chokcoco/pen/dymoOGN

emmm，又或者这样：

CSS Doodle - CSS Pattern 5

https://codepen.io/Chokcoco/pen/PoRqdYP

是的，我们可以把柏林噪声随机应用在各种属性上，我们可以放飞想象，去尝试各种不一样的搭配。下面这个， 就是把柏林噪声运用在点阵定位上：

<css-doodle grid="30x30">
    :doodle {
        @size: 90vmin;
        perspective: 10px;
    }
    position: absolute;
    top: 0;
    left: 0;
    width: 2px;
    height: 2px;
    border-radius: 50%;
    top: @rn(1%, 100%, 1.5);
    left: @rn(1%, 100%, 1.5);
    transform: scale(@rn(.1, 5, 2));
    background: hsl(@rn(1, 255, 3), @rn(10%, 90%), @rn(10%, 90%));
</css-doodle>

CodePen Demo -- CSS Doodle - CSS Pattern6

https://codepen.io/Chokcoco/pen/GRxJXVE

亦或者配合运用在 transform: rotate() 上：

<css-doodle grid="20x5">
    @place-cell: center;
    @size: calc(@i * 1.5%);
    :doodle {
        width: 60vmin; 
        height: 60vmin;
    }
    z-index: calc(999 - @i);
    border-radius: 50%;
    border: 1px @p(dashed, solid, double) hsl(@rn(255), 70%, @rn(60, 90%));
    border-bottom-color: transparent;
    border-left-color: transparent;
    transform: 
        rotate(@rn(-720deg, 720deg))
        scale(@rn(.8, 1.2, 3));
</css-doodle>

效果如下：

当然，每一次随机，都会是不一样的结果：

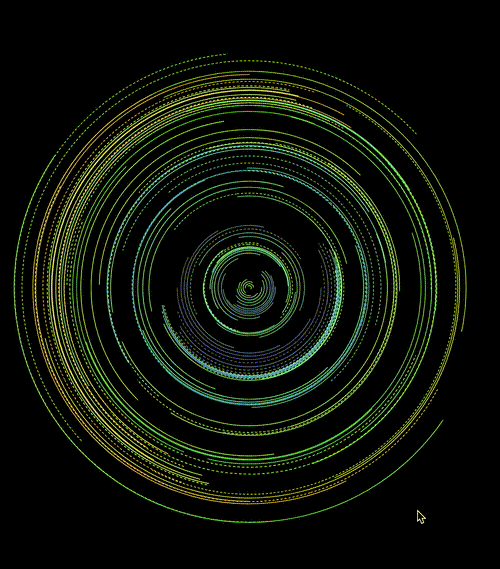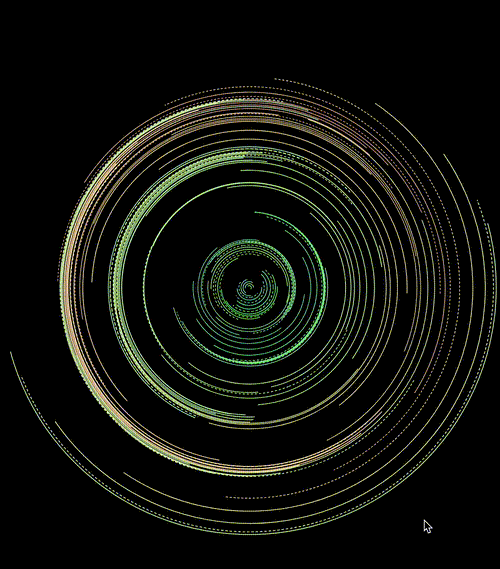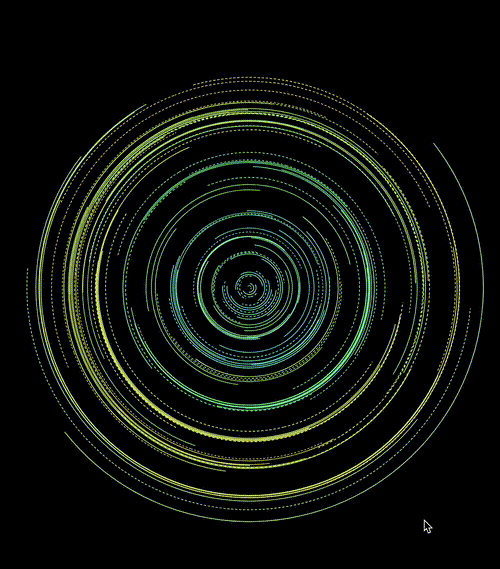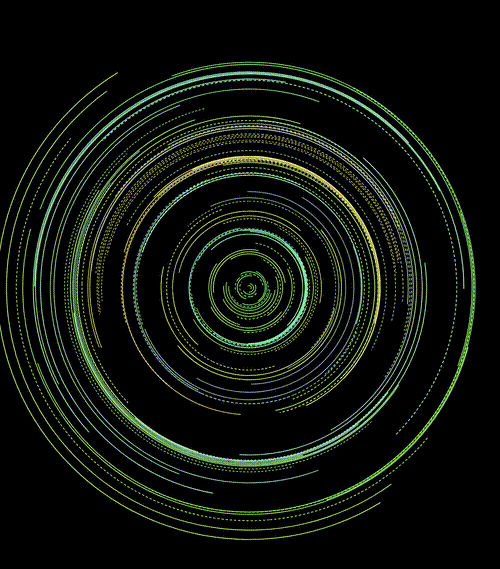
CodePen Demo -- CSS doodle - CSS Pattern7

https://codepen.io/Chokcoco/pen/ZExGjoy

好吧，我个人想象力有限，大家可以自行找到任一 DEMO，Fork 后自己去尝试碰撞出不一样的火花。

原文地址：https://segmentfault.com/a/1190000042103702

作者：chokcoco

（学习视频分享：web前端入门）

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!