Introduction détaillée aux arbres binaires JavaScript et à divers algorithmes de traversée

Cet article vous apporte des connaissances pertinentes sur javascript. Il présente principalement les détails des arbres binaires JavaScript et divers algorithmes de traversée. L'article fournit une introduction détaillée sur le sujet, qui a une certaine valeur de référence. . J'espère que cela aidera tout le monde.

[Recommandations associées : tutoriel vidéo javascript, front-end web]

Qu'est-ce qu'un arbre binaire

Un arbre binaire est un arbre dans lequel chaque nœud ne peut avoir qu'au plus deux nœuds enfants , comme le montre la figure ci-dessous :

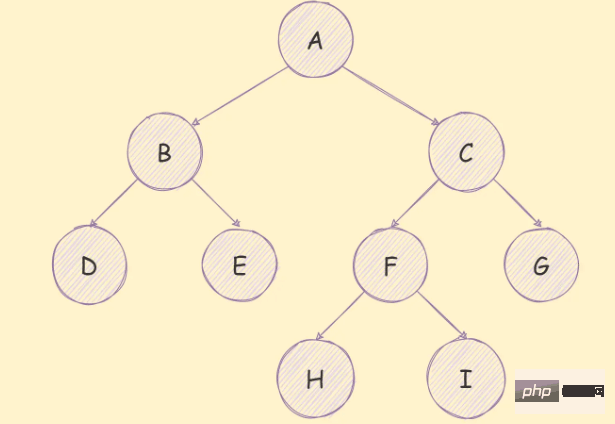
Un arbre binaire a les caractéristiques suivantes :

• La ième couche n'a au plus que 2^(i- 1) nœuds ; i层的节点最有只有2^(i-1)个；
• 如果这颗二叉树的深度为k，那二叉树最多有2^k-1个节点；
• 在一个非空的二叉树中，若使用n0表示叶子节点的个数，n2是度为2的非叶子节点的个数，那么两者满足关系n0 = n2 + 1。

满二叉树

如果在一个二叉树中，除了叶子节点，其余的节点的每个度都是2，则说明该二叉树是一个满二叉树，

如下图所示：

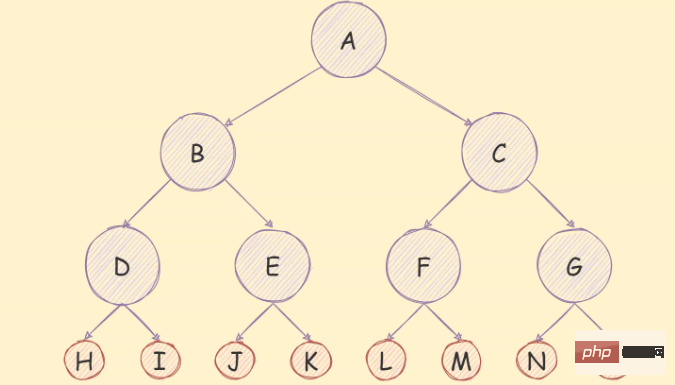
满二叉树除了满足普通二叉树特质，还具有如下几个特质：

• 满二叉树的的第n层具有2^(n-1)个节点；
• 深度为k的满二叉树一定存在2^k-1个节点，叶子节点的个数为2^(k-1)；
• 具有n个节点的满二叉树的深度为log_2^(n+1)。

完全二叉树

如果一个二叉树去掉最后一次层是满二叉树，且最后一次的节点是依次从左到右分布的，则这个二叉树是一个完全二叉树，

如下图所示：

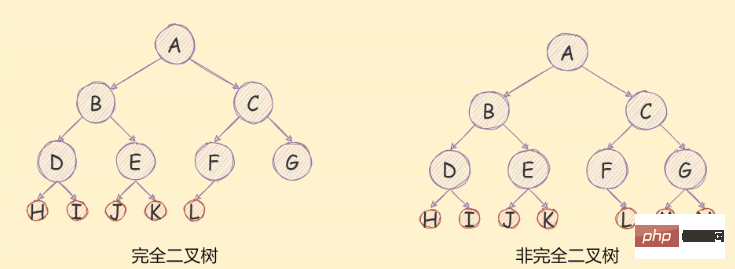
二叉树的存储

存储二叉树的常见方式分为两种，一种是使用数组存储，另一种使用链表存储。

数组存储

使用数组存储二叉树，如果遇到完全二叉树，存储顺序从上到下，从左到右，如下图所示：

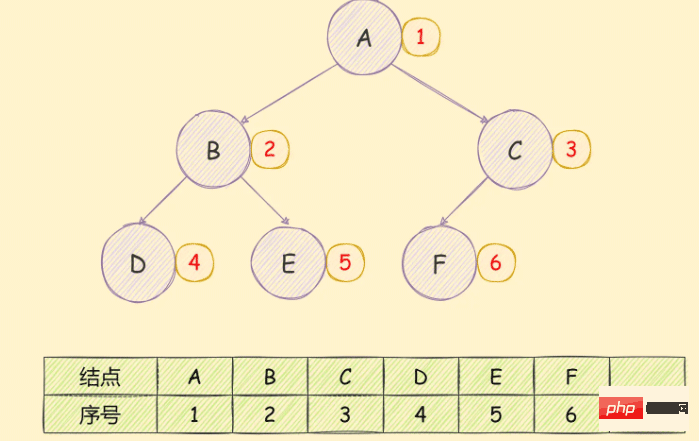
如果是一个非完全二叉树，如下图所示：

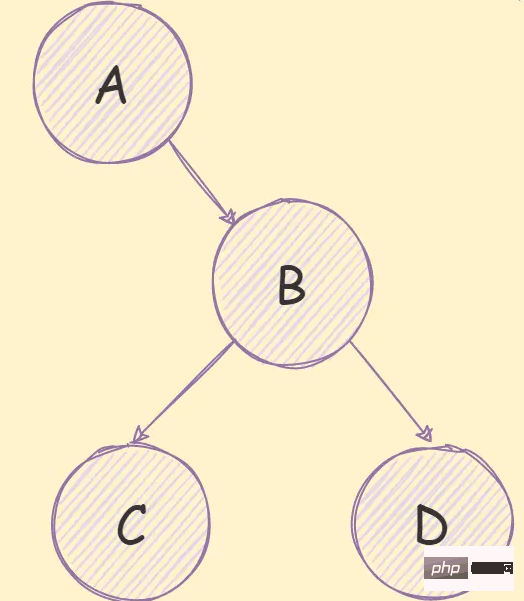
需要先将其转换为完全二叉树，然后在进行存储，如下图所示：

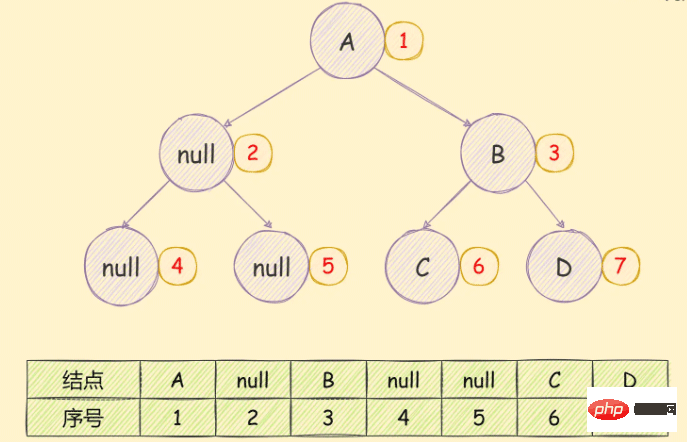
可以很明显的看到存储空间的浪费。

链表存储

使用链表存储通常将二叉树中的分为3个部分，如下图：

这三个部分依次是左子树的引用，该节点包含的数据，右子树的引用，存储方式如下图所示：

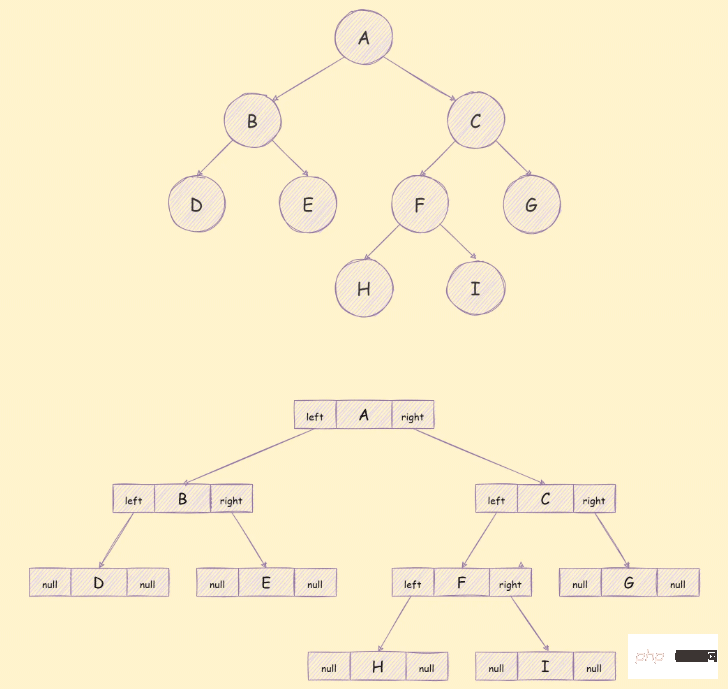
与二叉树相关的算法

以下算法中遍历用到的树如下：

// tree.js
const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}
module.exports = bt

深度优先遍历

二叉树的深度优先遍历与树的深度优先遍历思路一致，思路如下：

• 访问根节点；
• 访问根节点的left
• 访问根节点的right
• 重复执行第二三步

实现代码如下：

const bt = {
  val: 'A',
  left: {
    val: 'B',
    left: { val: 'D', left: null, right: null },
    right: { val: 'E', left: null, right: null },
  },
  right: {
    val: 'C',
    left: {
      val: 'F',
      left: { val: 'H', left: null, right: null },
      right: { val: 'I', left: null, right: null },
    },
    right: { val: 'G', left: null, right: null },
  },
}

function dfs(root) {
  if (!root) return
  console.log(root.val)
  root.left && dfs(root.left)
  root.right && dfs(root.right) 
}
dfs(bt)
/** 结果
A B D E C F H I G
*/

广度优先遍历

实现思路如下：

• 创建队列，把根节点入队
• 把对头出队并访问
• 把队头的left和right
Si la profondeur de cet arbre binaire est k, alors l'arbre binaire a au plus 2^k-1 nœuds ; Dans un arbre binaire non vide, si vous utilisez n0 représente le nombre de nœuds feuilles, n2 est le nombre de nœuds non feuilles de degré 2, alors les deux satisfont la relation n0 = n2 + 1.

Arbre binaire complet

Si dans un arbre binaire, À l'exception des nœuds feuilles, le degré de chaque nœud est 2, alors cela signifie que l'arbre binaire est un arbre binaire complet

,

Comme le montre le figure ci-dessous :

🎜🎜🎜En plus de satisfaire les caractéristiques des arbres binaires ordinaires, les arbres binaires complets ont également les caractéristiques suivantes : 🎜🎜🎜🎜Le nème niveau d'un arbre binaire complet a 2^(n-1)</code > nœuds ; 🎜🎜La profondeur est <code>k< L'arbre binaire complet de /code> doit avoir <code>2^k-1 nœuds, et le nombre de nœuds feuilles est 2^( k-1); 🎜🎜has La profondeur d'un arbre binaire complet avec n nœuds est log_2^(n+1). 🎜🎜🎜Arbre binaire complet🎜🎜🎜Si un arbre binaire est un arbre binaire complet après avoir supprimé la dernière couche et que le dernier nœud est distribué 🎜de gauche à droite, alors l'arbre binaire est un arbre binaire complet, 🎜🎜🎜comme illustré dans la figure ci-dessous : 🎜🎜🎜🎜🎜Stockage de arbres binaires🎜🎜Stockage des arbres binaires Il existe deux manières courantes, l'une consiste à utiliser le 🎜stockage en tableau🎜 et l'autre consiste à utiliser le stockage par liste chaînée. 🎜🎜Stockage en tableau🎜🎜🎜Utilisez des tableaux pour stocker des arbres binaires. Si vous rencontrez un arbre binaire complet, l'ordre de stockage est de haut en bas, de gauche à droite, comme indiqué dans la figure ci-dessous : 🎜🎜🎜🎜🎜🎜S'il s'agit d'un arbre binaire incomplet, comme indiqué ci-dessous : 🎜🎜🎜🎜🎜🎜Vous devez le convertir en complétez d'abord l'arbre binaire, puis stockez-le, comme indiqué dans la figure ci-dessous. -5.png"/>🎜🎜C'est clairement visible. Gaspillage d'espace de stockage. 🎜🎜Stockage de listes chaînées🎜🎜🎜En utilisant le stockage de listes chaînées, l'arborescence binaire est généralement divisée en 3 parties, comme indiqué ci-dessous : 🎜🎜🎜🎜🎜🎜Ces trois parties sont tour à tour la référence au sous-arbre de gauche, les données contenues dans le nœud, et la référence au sous-arbre de droite. Le stockage La méthode est comme indiqué dans la figure ci-dessous : 🎜🎜 🎜🎜 🎜Algorithmes liés aux arbres binaires🎜🎜🎜Les algorithmes suivants L'arbre utilisé dans le parcours est le suivant🎜 :🎜

function bfs(root) {
  if (!root) return
  const queue = [root]
  while (queue.length) {
    const node = queue.shift()
    console.log(node.val)
    node.left && queue.push(node.left)
    node.right && queue.push(node.right)
  }
}
bfs(bt)
/** 结果
A B C D E F G H I
 */

🎜Parcours en profondeur d'abord🎜🎜🎜Le parcours en profondeur d'abord d'un arbre binaire est cohérent avec le parcours en profondeur d'abord d'un arbre. L'idée est la suivante :🎜🎜🎜🎜Visiter le nœud racine 🎜🎜Visiter le < du code du nœud racine>gauche🎜🎜Accéder au droit de la racine ; node🎜🎜Répétez les deuxième et troisième étapes🎜🎜🎜🎜Le Code d'implémentation est le suivant:🎜🎜

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

🎜Breadth-first traversal🎜🎜🎜L'idée d'implémentation est la suivante：🎜🎜🎜🎜Créer une file d'attente et ajouter le noeud racine à la file d'attente🎜🎜Retirez l'adversaire et accédez-y🎜🎜Entrez la gauche et la droite en tête de la file d'attente dans l'ordre🎜🎜Répétez Exécutez les étapes 2 et 3 jusqu'à ce que le la file d'attente est vide🎜🎜🎜🎜Le code d'implémentation est le suivant :🎜🎜

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

🎜Parcours de pré-commande🎜🎜🎜L'idée d'implémentation du parcours de pré-commande d'un arbre binaire est la suivante :🎜🎜

• 访问根节点;
• 对当前节点的左子树进行先序遍历；
• 对当前节点的右子树进行先序遍历；

如下图所示：

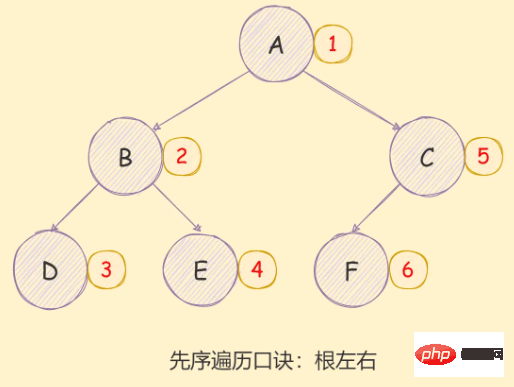
递归方式实现如下：

const bt = require('./tree')

function preorder(root) {
  if (!root) return
  console.log(root.val)
  preorder(root.left)
  preorder(root.right)
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

迭代方式实现如下：

// 非递归版
function preorder(root) {
  if (!root) return
  // 定义一个栈，用于存储数据
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    console.log(node.val)
    /* 由于栈存在先入后出的特性，所以需要先入右子树才能保证先出左子树 */
    node.right && stack.push(node.right)
    node.left && stack.push(node.left)
  }
}
preorder(bt)
/** 结果
A B D E C F H I G
*/

中序遍历

二叉树的中序遍历实现思想如下：

• 对当前节点的左子树进行中序遍历；
• 访问根节点;
• 对当前节点的右子树进行中序遍历；

如下图所示：

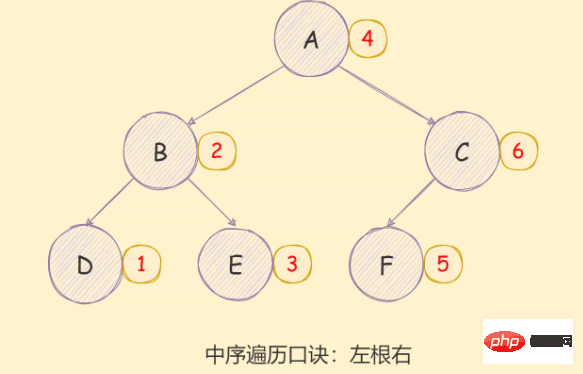
递归方式实现如下：

const bt = require('./tree')

// 递归版
function inorder(root) {
  if (!root) return
  inorder(root.left)
  console.log(root.val)
  inorder(root.right)
}
inorder(bt)

/** 结果
D B E A H F I C G
*/

迭代方式实现如下：

// 非递归版
function inorder(root) {
  if (!root) return
  const stack = []
  // 定义一个指针
  let p = root
  // 如果栈中有数据或者p不是null，则继续遍历
  while (stack.length || p) {
    // 如果p存在则一致将p入栈并移动指针
    while (p) {
      // 将 p 入栈，并以移动指针
      stack.push(p)
      p = p.left
    }

    const node = stack.pop()
    console.log(node.val)
    p = node.right
  }
}
inorder(bt)
/** 结果
D B E A H F I C G
*/

后序遍历

二叉树的后序遍历实现思想如下：

• 对当前节点的左子树进行后序遍历；
• 对当前节点的右子树进行后序遍历；
• 访问根节点;

如下图所示：

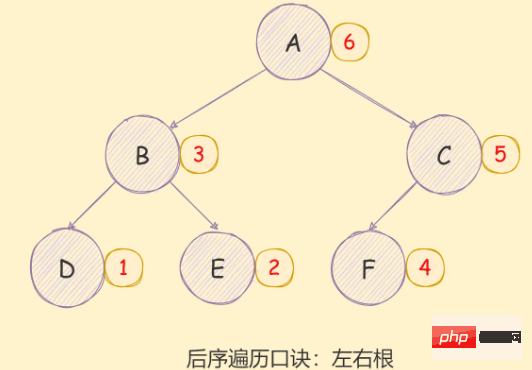
递归方式实现如下：

const bt = require('./tree')

// 递归版
function postorder(root) {
  if (!root) return
  postorder(root.left)
  postorder(root.right)
  console.log(root.val)
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

迭代方式实现如下：

// 非递归版
function postorder(root) {
  if (!root) return
  const outputStack = []
  const stack = [root]
  while (stack.length) {
    const node = stack.pop()
    outputStack.push(node)
    // 这里先入left需要保证left后出，在stack中后出，就是在outputStack栈中先出
    node.left && stack.push(node.left)
    node.right && stack.push(node.right)
  }
  while (outputStack.length) {
    const node = outputStack.pop()
    console.log(node.val)
  }
}
postorder(bt)
/** 结果
D E B H I F G C A
*/

【相关推荐：javascript视频教程、web前端】

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!