Cet article vous apporte des connaissances pertinentes sur java, qui présente principalement la transformation des fonctions aléatoires en Java. L'exemple de code dans l'article est expliqué en détail, ce qui nous est utile pour apprendre Java. Si vous êtes intéressé, vous pouvez. apprendre encore plus .
Étude recommandée : "Tutoriel vidéo Java"
En Java, la fonction Math.random() renvoie un intervalle avec une probabilité égale Toute décimale dans [0,1). Autrement dit, dans le cas de x < 1, la probabilité que le nombre dans [0,x) apparaisse est x. voulez changer x < 1, la probabilité du nombre dans [0,x) est ajustée à x^2 . Que faut-il faire ? Math.random()函数是等概率返回区间[0,1)中的任意一个小数。即x < 1情况下，[0,x)中的数出现的的概率是x，如果我们要将x < 1情况下，[0,x)中的数出现的的概率调整成x^2，应该如何做？
问题1思路
由于[0,x)的概率是x，那么调用两次Math.random()，如果较大的那个值也要在[0,x)区间内，那么两次调用都必须在[0,x)区间内（因为任意一次在[x,1)都会导致返回值不在[0,x)上），即概率是x^2，代码如下
package snippet;
public class Code_0004_RandToPow2 {
// 将`[0,x)`中的数出现的的概率调整成`x^2`
public static double randToPow2() {
return Math.max(Math.random(), Math.random());
}
}我们可以通过如下测试代码来验证问题1的解法：
package snippet;
public class Code_0004_RandToPow2 {
// 将`[0,x)`中的数出现的的概率调整成`x^2`
public static double randToPow2() {
return Math.max(Math.random(), Math.random());
}
// 测试用例
public static void main(String[] args) {
int count = 0;
int testTimes = 10000000;
double x = 0.17;
for (int i = 0; i < testTimes; i++) {
if (randToPow2() < x) {
count++;
}
}
System.out.println((double) count / (double) testTimes);
System.out.println(Math.pow(x, 2));
}
}打印的结果如下
0.0288603
0.028900000000000006
接近目标要求。
假设我们有一个随机函数f()，这个函数可以等概率返回[1,5]中的一个数，如何只利用f()函数而不引入其他随机函数，得到一个等概率返回[1,7]中任意一个数的函数g()。
思路
由于目标是求[1,7]等概率返回一个，如果我们能加工得到一个x()函数，这个函数是等概率返回[0,6]范围内的任意一个数，那么目标函数g()只需要调用这个x()函数再加上1，即是g()函数要求
public static int g() {
return x() + 1;
}要得到[0,6]等概率返回一个数，我们需要先得到一个0和1等概率返回的随机函数m()，我们可以通过f()函数来得到，即
// 通过[0,5]等概率返回的随机函数f()
// 加工出等概率得到0和1
// 1,2,3,4,5 五个数
// 得到1，2的时候，返回0
// 得到4，5的时候，返回1
// 得到3的时候，弃而不用，再次尝试
public static int m() {
int ans = 0;
do {
ans = f();
} while (ans == 3);
return ans < 3 ? 0 : 1;
}有了等概率返回 0 和 1 的随机函数 m()， 我们可以很方便的生成[0,6]随机等概率返回一个数的方法，因为[0,6]需要三个二进制数表示，那么我们可以调用三次m()函数，可以等概率得到[0,7]范围内任意一个数，我们可以在得到 7 的时候，重试上述过程，只有结果在[0,6]才返回，这样就加工出了x()函数。
// 等概率返回0~6
public static int x() {
int ans = 0;
do {
ans = (m() << 2) + (m() << 1) + m();
} while (ans == 7);
return ans;
}最后，目标函数f()通过如下方式
// 等概率返回1~7
public static int g() {
return x() + 1;
}即可得到。完整代码如下
package snippet;
public class Code_0005_Rand5ToRand7 {
// 此函数只能用，不能修改
// 等概率返回1~5
public static int f() {
return (int) (Math.random() * 5) + 1;
}
// 通过[0,5]等概率返回的随机函数f()
// 加工出等概率得到0和1
// 1,2,3,4,5 五个数
// 得到1，2的时候，返回0
// 得到4，5的时候，返回1
// 得到3的时候，弃而不用，再次尝试
public static int m() {
int ans = 0;
do {
ans = f();
} while (ans == 3);
return ans < 3 ? 0 : 1;
}
// 等概率返回0~6
public static int x() {
int ans = 0;
do {
ans = (m() << 2) + (m() << 1) + m();
} while (ans == 7);
return ans;
}
// 等概率返回1~7
public static int g() {
return x() + 1;
}
}
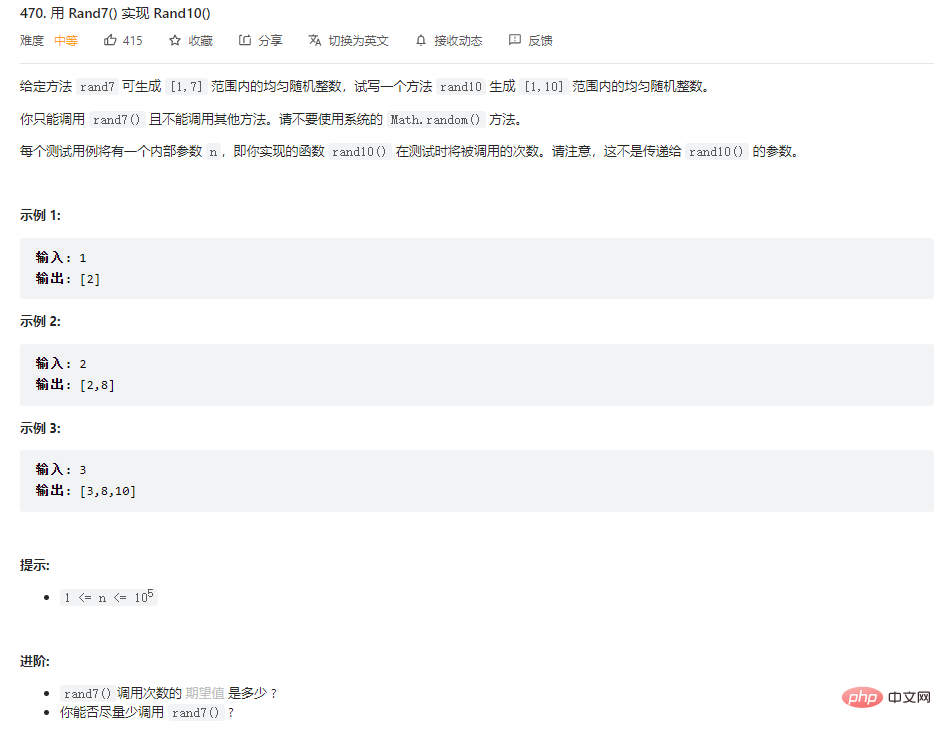
和问题2思路一致，核心都是要先实现一个等概率返回 0 和 1 的随机函数m()。，然后看目标函数区间需要几个二进制位，来决定调用几次m()函数，不赘述，完整代码见
/**
* The rand7() API is already defined in the parent class SolBase.
* public int rand7();
* @return a random integer in the range 1 to 7
*/
class Solution extends SolBase {
public int rand10() {
return rand(10);
}
public int rand(int N) {
int bit = 1;
int base = 2;
while (base <= N) {
base = 2 << bit;
bit++;
}
int v = build(bit);
while (v < 1 || v > N) {
v = build(bit);
}
return v;
}
private int build(int bit) {
int v = 0;
for (int i = 0; i < bit; i++) {
v += (m() << i);
}
return v;
}
// 核心：生成 0 和 1 等概率返回的随机函数
public int m() {
int i = rand7();
while (i == 7) {
i = rand7();
}
return (i == 1 || i == 2 || i == 3) ? 0 : 1;
}
}有一个函数f()，不等概率（但是是固定概率）返回0和1，如何只通过f()函数，得到等概率返回 0 和 1 的随机函数g()，
思路，
调用两次f()函数，可以得到如下情况
0 0
1 1
0 1
1 0
当两次都是0，或者两次都是1的时候，舍弃，虽然 0 和 1 的概率不一样，但是
0 1
1 0
概率一定一样
所以得到 0 1就返回 0 ，得到 1 0就返回1，即g()
[0,x) est x, alors appelez Math.random() deux fois. Si la valeur la plus grande doit également être dans l'intervalle [0,x), les deux appels doivent donc être dans l'intervalle [0,x) (car à tout moment dans l'intervalle < code>[0,x) interval code>[x,1) fera en sorte que la valeur de retour ne soit pas sur [0,x)), c'est-à-dire que le la probabilité est x^2, le code est le suivant package snippet;
// 不等概率随机函数变成等概率随机函数
public class Code_0005_EqualProbabilityRandom {
// 不等概率函数，
// 内部内容不可见
public static int f() {
return Math.random() < 0.8 ? 0 : 1;
}
// 等概率返回0和1
public static int g() {
int first;
do {
first = f(); // 0 1
} while (first == f());
return first;
}
}🎜0.0288603🎜Proche des exigences cibles. 🎜
0.028900000000000006🎜
f() Cette fonction peut renvoyer un nombre dans [1,5] avec une probabilité égale. , comment utiliser uniquement la fonction f() sans introduire d'autres fonctions aléatoires, et obtenir une probabilité égale de renvoyer n'importe quel nombre dans [1,7] code> La fonction <code>g(). 🎜🎜Idée🎜🎜Puisque le but est de renvoyer [1,7] avec une probabilité égale, si nous pouvons traiter une fonction x(), cette fonction reviendra avec une probabilité égale probabilité N'importe quel nombre compris dans la plage de [0,6], alors la fonction cible g() n'a besoin que d'appeler cette fonction x() plus 1, c'est-à-dire que la fonction g() nécessite 🎜rrreee🎜 pour que [0,6] renvoie un nombre avec une probabilité égale, nous devons obtenez d'abord un 0 et un 1 La fonction aléatoire m() qui renvoie une probabilité égale peut être obtenue via la fonction f(), c'est-à-dire 🎜rrreee 🎜 a une probabilité égale de renvoyer 0 et 1 La fonction aléatoire m(), nous pouvons facilement générer [0,6] une méthode pour renvoyer aléatoirement un nombre avec une probabilité égale, parce que [0,6] Nous avons besoin de trois nombres binaires à représenter, alors nous pouvons appeler la fonction m() trois fois, et nous pouvons obtenir n'importe quel nombre dans la plage de [0,7] avec une probabilité égale. Nous pouvons réessayer le processus ci-dessus lorsque nous obtenons 7, et seul le résultat est renvoyé lorsque [0,6], traitant ainsi le Fonction x(). 🎜rrreee🎜Enfin, la fonction objectif f() peut être obtenue comme suit 🎜rrreee🎜. Le code complet est le suivant🎜rrreee
🎜🎜L'idée est la même que celle de la question 2. L'essentiel est ded'abord implémenter une fonction aléatoire m() qui renvoie 0 et 1 avec une probabilité égale. , puis regardez combien de bits binaires sont nécessaires dans l'intervalle de la fonction cible pour décider combien de fois appeler la fonction m(). Je n'entrerai pas dans les détails. code complet, voir 🎜rrreee
f() qui renvoie 0 et 1 avec une probabilité inégale (mais une probabilité fixe). Comment obtenir une probabilité égale de). renvoyer 0 et 1 uniquement via la fonction f() ? La fonction aléatoire g() de 1, 🎜🎜idée, 🎜🎜appelle le f() deux fois, vous pouvez obtenir la situation suivante 🎜<blockquote>🎜0 0<br>1 1<br>0 1<br>1 0🎜</blockquote>🎜Quand les deux temps sont 0, ou les deux temps sont 1, jetez-les. Bien que les probabilités de 0 et 1 soient différentes, 🎜 <blockquote>🎜0 1<br>1 0🎜</blockquote>🎜La probabilité doit être la même🎜🎜, donc si vous obtenez. <code>0 1, vous retournerez 0, si vous obtenez 1 0, vous retournerez 1. La fonction g()🎜🎜Le code complet est la suivante🎜rrreee🎜Apprentissage recommandé : "🎜Tutoriel vidéo Java🎜"🎜Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
![Analyse approfondie de JavaScript [Le front-end Web doit connaître les compétences de base]](https://img.php.cn/upload/course/000/000/041/61d3ff1c83b43350.jpg)
![Vidéo d'introduction à TypeScript [peut être comprise même sans apprendre JavaScript]](https://img.php.cn/upload/course/000/000/068/6242c0fc4be39373.png)
![Développement pratique de l'imitation Meituan APP [Un projet JavaScript incontournable pour les programmeurs front-end]](https://img.php.cn/upload/course/000/000/068/6242bebc05ca9210.png)
![[Web front-end] Démarrage rapide de Node.js](https://img.php.cn/upload/course/000/000/067/662b5d34ba7c0227.png)
