Illustration du principe et de la mise en œuvre de la recherche binaire de l'algorithme classique Java

Cet article vous apporte des connaissances pertinentes sur java. La méthode de demi-recherche est également appelée recherche binaire. Comme son nom l'indique, elle divise les données en deux moitiés, puis détermine dans quelle moitié se trouve la clé, puis répète ce qui précède. Étapes Maintenant que vous avez trouvé la clé cible, examinons-la. J'espère qu'elle sera utile à tout le monde.

Apprentissage recommandé : "Tutoriel vidéo Java"

Recherche binaire

La recherche binaire est également appelée recherche binaire (Recherche binaire) C'est une méthode de recherche plus efficace qui peut être utilisée dans le logarithme des données. taille. Terminez la recherche dans la complexité temporelle. Il s'agit d'un algorithme de recherche permettant de trouver un élément spécifique dans un tableau ordonné.

Idée d'algorithme

Prenons la séquence ascendante comme exemple, comparez la taille de l'élément cible et de l'élément au milieu de la séquence, si l'élément cible est plus grand que l'élément du milieu, continuez à effectuer une recherche binaire dans la seconde moitié de la séquence ; si l'élément cible S'il est plus petit que l'élément en position médiane, la comparaison est faite dans la première moitié du tableau ; s'ils sont égaux, la position de l'élément est trouvée ; La longueur du tableau pour chaque comparaison sera la moitié du tableau précédent jusqu'à ce que la position des éléments égaux soit trouvée ou que l'élément cible ne soit pas trouvé.

Illustration

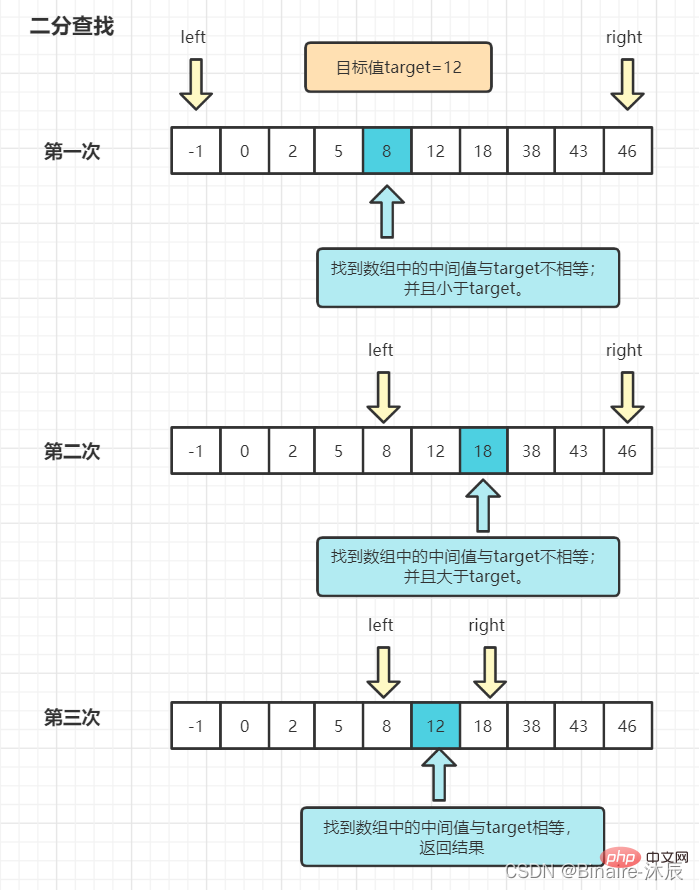
Étant donné un tableau ordonné par ordre croissant nums=[-1, 0, 2, 5, 8, 12, 18, 38, 43, 46]

Ensuite, trouvez la valeur cible cible dans le tableau =12.

Le diagramme est le suivant :

Proche de la question d'origine

Portail

Description du problème :

Étant donné un nombre de tableaux d'entiers ordonnés (ascendants) à n éléments et une valeur cible cible, écrivez une fonction Rechercher pour la cible en chiffres et renvoie l'indice si la valeur cible existe, sinon -1.

Exemple 1 :

Entrée : nums = [-1,0,3,5,9,12], cible = 9
Sortie : 4
Explication : 9 apparaît en chiffres et l'indice est 4

Exemple 2 :

Entrée : nums = [-1,0,3,5,9,12], cible = 2
Sortie : -1
Explication : 2 n'existe pas en nums, donc -1 est renvoyé

Résoudre le problème Idée :

Selon le sens de la question, on peut conclure que le tableau est un tableau ordonné, ce qui est également une condition préalable à l'utilisation de la recherche binaire.

• Définissez deux pointeurs pointant respectivement vers le premier et le dernier élément du tableau ;
• Trouvez la valeur médiane au milieu du tableau ;
• Si nums[mid] < est situé dans la seconde moitié de la partie du tableau, sinon <code>nums[mid] > target est dans la première moitié nums[mid] < target，则 target 位于数组的后半部分，反之nums[mid] > target在前半部分；
• 重复上一步操作，直到nums[mid] = target
Répétez l'étape précédente jusqu'à ce que nums[mid] = target; code>, indiquant que la cible est trouvée et que l'indice est renvoyé. C'est tout.

Implémentation du code Java :

class Solution {
    public int search(int[] nums, int target) {
        int left = 0,right = nums.length - 1;
        while(left <= right) { // 循环条件
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                return mid;
            } else if (nums[mid] < target) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        }
        return -1;  // 找不到则返回-1
    }
}

Analyse de complexité :

• Complexité temporelle : O(logn), où n est la longueur du tableau.
• Complexité spatiale : O(1).

Apprentissage recommandé : "Tutoriel vidéo Java

"🎜

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!