 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Augmentez vos connaissances! Apprentissage automatique avec des règles logiques
Augmentez vos connaissances! Apprentissage automatique avec des règles logiques
Augmentez vos connaissances! Apprentissage automatique avec des règles logiques
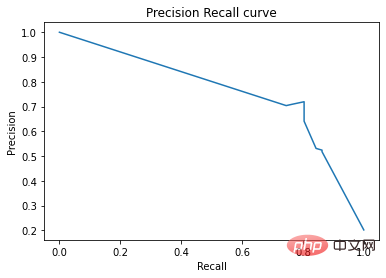
Sur la courbe précision-rappel, les mêmes points sont tracés avec des axes différents. Attention : Le premier point rouge à gauche (0% de rappel, 100% de précision) correspond à 0 règle. Le deuxième point à gauche est la première règle, et ainsi de suite.
Skope-rules utilise un modèle d'arborescence pour générer des règles candidates. Créez d’abord des arbres de décision et considérez les chemins allant du nœud racine aux nœuds internes ou aux nœuds feuilles comme candidats aux règles. Ces règles candidates sont ensuite filtrées selon certains critères prédéfinis tels que la précision et le rappel. Seuls ceux dont la précision et le rappel sont supérieurs à leurs seuils sont retenus. Enfin, un filtrage de similarité est appliqué pour sélectionner des règles présentant une diversité suffisante. En général, les règles Skope sont appliquées pour apprendre les règles sous-jacentes à chaque cause fondamentale.
Adresse du projet : https://github.com/scikit-learn-contrib/skope-rules
- Skope-rules est un module d'apprentissage automatique Python construit sur scikit-learn, sous BSD à 3 clauses Publié avec autorisation.
- Skope-rules vise à apprendre des règles logiques et interprétables pour "définir" la catégorie cible, c'est-à-dire détecter les instances de cette catégorie avec une grande précision.
- Les règles Skope sont un compromis entre l'interprétabilité des arbres de décision et les capacités de modélisation des forêts aléatoires.
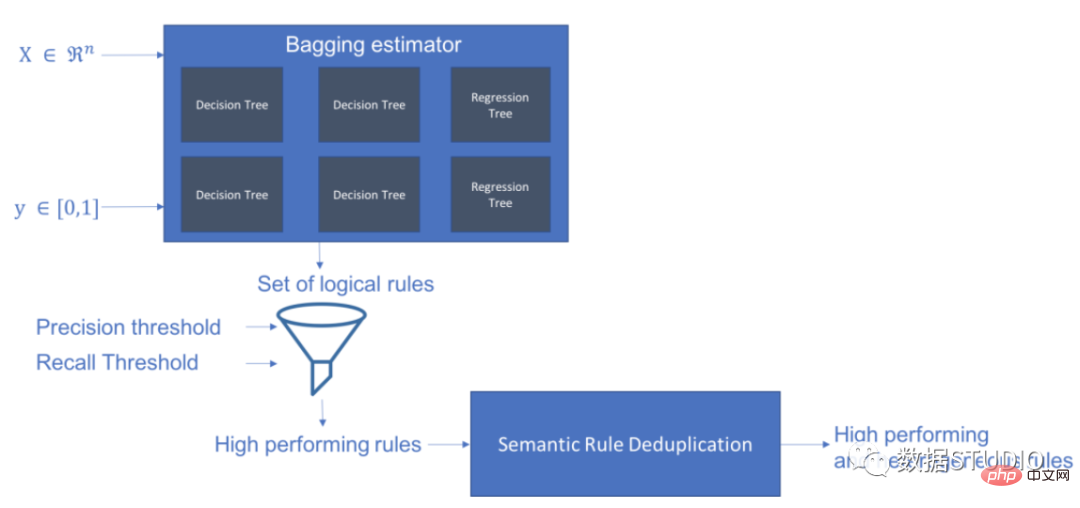
schema
Installation
Vous pouvez utiliser pip pour obtenir les dernières ressources :
pip install skope-rules
Démarrage rapide
SkopeRules peut être utilisé pour décrire des classes avec des règles logiques :
from skle arn .datasets import load_iri s UFrom Skrules Import Skoperules
dataset = load_iris ()
feature_names = ['SEPAL_LENGTH', 'SEPAL_WIDTH', 'Petal_length'] KClf = Skoperules (MAX_DEPTH_DUPLICATINOTALOW = 2,
n_estimators = 30, précision_min = 0,3 ,
rappel_min=0.1,
feature_names=feature_names)
pour idx, espèces dans enumerate(dataset.target_names) :
X, y = dataset.data, dataset.target
clf.fit(X, y == idx)
règles = clf.rules_[0:3]
print("Règles pour l'iris", espèce)
pour la règle dans les règles :
print(rule)
print()
print(20*'=')
print()
Remarque : 
Solution : 
import sys
sys.modules['sklearn.externals.six'] = siximport mlrose
Le test personnel est valide !
SkopeRules peut également être utilisé comme prédicteurs si vous utilisez la méthode "score_top_rules":
from sklearn.metrics import précision_recall_curve
from matplotlib import pyplot as pltfrom skrules import SkopeRules
dataset = pierre( )
clf = SkopeRules(max_degree_duplicatinotallow=Aucun,
n_estimators=30,
précision_min=0.2,
rappel_min=0.01,
feature_names=dataset.feature_names)
X, y = dataset.data, dataset.target > , y_train = X[:len(y)//2], y[:len(y)//2]
X_test, y_test = X[len(y)//2:], y[len(y)/ /2:]
clf.fit(X_train, y_train)
y_score = clf.score_top_rules(X_test) # Obtenez un score de risque pour chaque exemple de test
precision, rappel, _ = précision_recall_curve(y_test, y_score)
plt.plot(recall , précision)
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.title('Precision Recall curve')
plt.show()
Cas pratique
 Cet étui présente Utilisation de règles de portée sur le célèbre ensemble de données Titanic.
Cet étui présente Utilisation de règles de portée sur le célèbre ensemble de données Titanic.
situation applicable aux règles skope :
- Résoudre le problème de classification binaire
- Extraire des règles de décision interprétables
Ce cas est divisé en 5 parties
- Importer des bibliothèques pertinentes
- Préparation des données
- Formation du modèle (en utilisant la méthode ScopeRules().score_top_rules())
- Explication des "Règles de survie" (en utilisant SkopeRules().rules_property).
- Analyse des performances (en utilisant la méthode SkopeRules.predict_top_rules()).
Importer des bibliothèques associées
# Importer des règles skope
à partir de skrules importer SkopeRules
# Importer des bibliothèques
importer des pandas au format pd
à partir de sklearn.ensemble importer GradientBoostingClassifier, RandomForestClassifier
à partir de sklearn.model_selection importer train_test_split
à partir de l'importation de sklearn.tree DecisionTreeClassifier
importer matplotlib.pyplot en tant que plt
depuis sklearn.metrics importer roc_curve, précision_recall_curve
depuis matplotlib importer cm
importer numpy en tant que np
depuis sklearn.metrics importer confusion_matrix
depuis IPython.display importer display
# Importer des données Titanic
data = pd.read_csv('../data/titanic-train.csv')
Préparation des données
# Supprimer les lignes avec l'âge manquant
data = data.query('Age == Age')
# Créer un encodage pour la variable Sexe Valeur
data['isFemale'] = (data['Sex'] == 'female') * 1
# Unvaried Embarked crée une valeur codée
data = pd.concat(
[data,
pd.get_dummies(data. loc [:,'Embarked'],
dummy_na=False,
prefix='Embarked',
prefix_sep='_')],
axis=1
)
# Supprimer les variables inutilisées
data = data.drop( ['Name ', 'Ticket', 'Cabine',
'PassengerId', 'Sex', 'Embarked'],
axis = 1)
# Créer des ensembles de formation et de test
X_train, X_test, y_train, y_test = train_test_split(
data. drop(['Survived'], axis=1),
data['Survived'],
test_size=0.25, random_state=42)
feature_names = X_train.columns
print('Les noms de colonnes sont : ' + ' '. join(feature_names.tolist())+'.')
print('La forme de l'ensemble d'entraînement est : ' + str(X_train.shape) + '.')
Les noms de colonnes sont : Pclass Age SibSp Parch Fare
isFemale Embarked_C Embarked_Q Embarked_S.
La forme de l'ensemble de formation est : (535, 9).
Formation du modèle
# Former un classificateur d'amélioration de gradient pour les tests de référence
gradient_boost_clf = GradientBoostingClassifier(random_state=42, n_estimators=30, max_degree = 5)
gradient_boost_clf .fit(X_train, y_train)
# Entraîner un classificateur de forêt aléatoire pour l'analyse comparative
random_forest_clf = RandomForestClassifier(random_state=42, n_estimators=30, max_degree = 5)
random_forest_clf.fit(X_train, y_train)
# Entraîner un arbre de décision classificateur pour l'analyse comparative
decision_tree_clf = DecisionTreeClassifier(random_state=42, max_degree = 5)
decision_tree_clf.fit(X_train, y_train)
# Former une classification skope-rules-boosting
skope_rules_clf = SkopeRules(feature_names=feature_names, 2, n_estimateurs =30,
rappel_min=0,05, précision_min=0,9,
max_samples=0,7,
max_degree_duplicatinotallow= 4, max_degree = 5)
skope_rules_clf.fit(X _train, y_train)
# Calculer le score de prédiction
gradient_boost_scoring = gradient_boost _clf.predict_proba( X_test)[:, 1]
random_forest_scoring = random_forest_clf.predict_proba(X_test)[:, 1]
decision_tree_scoring = décision_tree_clf.predict_proba(X_test )[:, 1]
skope_rules_scoring = skope_rules_clf.score_top_rules ( ")
# Imprimer ces règles
rules_explanations = [ "Femme de moins de 3 ans et de moins de 37 ans en première ou deuxième classe. "
"Femme âgée de 3 ans et plus voyageant en première ou deuxième classe et payant plus de 26 euros. "
"Femme qui voyage en première ou en deuxième classe et paie plus de 29 euros. "
"Femme de plus de 39 ans voyageant en première ou en deuxième classe. "
]
print('Les quatre "règles de survie du Titanic" les plus performantes sont les suivantes :/n')
pour i_rule, règle dans enumerate(skope_rules_clf.rules_[:4])
print(rule[ 0])
print('->'+rules_explanations[i_rule]+ 'n')
Utiliser SkopeRules pour créer 9 règles
Les 4 meilleures "Règles de survie du Titanic" sont les suivantes :
Âge et Pclass 0,5
-> Femmes de moins de 3 ans et de moins de 37 ans, en première ou deuxième classe
Âge > ;= 2,5 et isFemme > 0,5
-> Les femmes de plus de 3 ans voyageant en première ou en deuxième classe et payant plus de 26 euros.
Tarif > 29,356250762939453
et Pclass 0,5
->
Âge > 38,5 et Pclass et estFemme > 0,5
-> Les femmes de plus de 39 ans voyageant en première ou en deuxième classe.
def calculate_y_pred_from_query(X, règle):
score = np.zeros(X.shape[0])
X = X.reset_index(drop=True)
score[list(X.query(rule).index)] = 1
return(score)
def calculate_performances_from_y_pred(y_true, y_pred, index_name='default_index'):
df = pd.DataFrame(data=
{
'precision':[sum(y_true * y_pred)/sum(y_pred )],
'recall':[sum(y_true * y_pred)/sum(y_true)]
},
index=[index_name],
columns=['precision', 'recall']
)
return(df) " from_y_pred( y_test, y_test_pred, 'test_set')],
axis=0)
return(performances)
print('Précision = 0,96 signifie que 96% des personnes identifiées par la règle sont des survivants.')
print(' Rappel = 0,12 signifie que les survivants identifiés par la règle représentent 12% du total des survivants')
for i in range(4):
print('Rule '+str(i+1)+':')
display(compute_train_test_query_performances(X_train, y_train,
X_test, y_test,
skope_rules_clf.rules_[i][ 0])
)
Precision = 0,96 signifie que 96 % des personnes déterminées par les règles sont des survivants.
Recall = 0,12 signifie que les survivants identifiés par la règle représentent 12 % du total des survivants.
Tests de performances du modèle
def plot_titanic_scores(y_true, scores_with_line=[], scores_with_points=[],
labels_with_line=['Gradient Boosting', 'Random Forest', 'Decision Tree'],
labels_with_points=[ 'skope-rules']):
gradient = np.linspace(0, 1, 10)color_list = [ cm.tab10(x) pour x en dégradé]
fig, axes = plt.subplots(1, 2, figsize=(12, 5), sharex=True, sharey=True)
n_line = 0 pour i_score, score en enumerate(scores_with_line):
pour i_score, score en enumerate(scores_with_line):
fpr, tpr, _ = roc_curve(y_true, score)
ax.plot(fpr, tpr, linestyle='-.', c=color_list[i_score], lw=1, label=labels_with_line[i_score])pour i_score, score en énumération( scores_with_points):
fpr, tpr, _ = roc_curve(y_true, score)
ax.scatter(fpr[:-1], tpr[:-1], c=color_list[n_line + i_score], s=10, label= labels_with_points[i_score])
ax.set_title("ROC", fnotallow=20)
ax.set_xlabel('Taux de faux positifs', fnotallow=18)
ax.set_ylabel('Taux de vrais positifs (rappel)', fnotallow=18 )
ax.legend(loc='lower center', fnotallow=8)
ax = axes[1]
n_line = 0
pour i_score, score en énumération(scores_with_line):
n_line = n_line + 1
précision, rappel , _ = précision_recall_curve(y_true, score)
ax.step(recall, précision, linestyle='-.', c=color_list[i_score], lw=1,where='post', label=labels_with_line[i_score])
pour i_score, score en enumerate(scores_with_points):
precision, rappel, _ = précision_recall_curve(y_true, score)
ax.scatter(recall, précision, c=color_list[n_line + i_score], s=10, label=labels_with_points[i_score ])
ax.set_title("Precision-Recall", fnotallow=20)
ax.set_xlabel('Rappel (taux positif réel)', fnotallow=18)
ax.set_ylabel('Precision', fnotallow=18)
ax .legend(loc='lower center', fnotallow=8)
plt.show()
plot_titanic_scores(y_test,
scores_with_line=[gradient_boost_scoring, random_forest_scoring, decision_tree_scoring],
scores_with_points=[skope_rules_scoring]
)
Sur la courbe ROC, chaque point rouge correspond au nombre de règles activées (issues de skope-rules). Par exemple, le point le plus bas est le point résultat d’une règle (la meilleure). Le deuxième point le plus bas est le point de résultat des 2 règles, et ainsi de suite.
Sur la courbe précision-rappel, les mêmes points sont tracés avec des axes différents. Attention : Le premier point rouge à gauche (0% de rappel, 100% de précision) correspond à 0 règle. Le deuxième point à gauche est la première règle, et ainsi de suite.
Certaines conclusions peuvent être tirées de cet exemple.
- les règles skope fonctionnent mieux que les arbres de décision.
- les règles de skope fonctionnent de la même manière que l'amélioration aléatoire de la forêt/du dégradé (dans cet exemple).
- L'utilisation de 4 règles permet d'obtenir de très bonnes performances (61 % de rappel, 94 % de précision) (dans cet exemple).
n_rule_chosen = 4
y_pred = skope_rules_clf.predict_top_rules(X_test, n_rule_chosen)
print('Les performances atteintes avec '+str(n_rule_chosen)+' les règles découvertes sont les suivantes :')
compute_performances_from_y_pred(y_test, _pred, ' test_set')
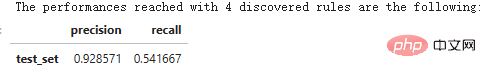
predict_top_rules(new_data, n_r) est utilisée pour calculer la prédiction de new_data, qui contient les premières règles de skope-rules n_r.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Mise à jour OpenOOD v1.5 : bibliothèque de codes de détection hors distribution complète et précise et plateforme de test, prenant en charge les classements en ligne et les tests en un clic
Jul 03, 2023 pm 04:41 PM
Mise à jour OpenOOD v1.5 : bibliothèque de codes de détection hors distribution complète et précise et plateforme de test, prenant en charge les classements en ligne et les tests en un clic
Jul 03, 2023 pm 04:41 PM
La détection hors distribution (OOD) est cruciale pour le fonctionnement fiable des systèmes intelligents en monde ouvert, mais les méthodes actuelles de détection orientée objet souffrent d'« incohérences d'évaluation » (incohérences d'évaluation). Travaux antérieurs OpenOODv1 unifie l'évaluation de la détection OOD, mais présente toujours des limites en termes d'évolutivité et de convivialité. Récemment, l'équipe de développement a de nouveau proposé OpenOODv1.5. Par rapport à la version précédente, la nouvelle évaluation de la méthode de détection OOD a été considérablement améliorée pour garantir la précision, la standardisation et la convivialité. Document d'image : https://arxiv.org/abs/2306.09301OpenOODCodebase:htt
 Augmentez vos connaissances! Apprentissage automatique avec des règles logiques
Apr 01, 2023 pm 10:07 PM
Augmentez vos connaissances! Apprentissage automatique avec des règles logiques
Apr 01, 2023 pm 10:07 PM
Sur la courbe précision-rappel, les mêmes points sont tracés avec des axes différents. Attention : Le premier point rouge à gauche (0% de rappel, 100% de précision) correspond à 0 règle. Le deuxième point à gauche est la première règle, et ainsi de suite. Skope-rules utilise un modèle d'arborescence pour générer des règles candidates. Créez d’abord des arbres de décision et considérez les chemins allant du nœud racine aux nœuds internes ou aux nœuds feuilles comme candidats aux règles. Ces règles candidates sont ensuite filtrées selon certains critères prédéfinis tels que la précision et le rappel. Seuls ceux dont la précision et le rappel sont supérieurs à leurs seuils sont retenus. Enfin, un filtrage de similarité est appliqué pour sélectionner des règles présentant une diversité suffisante. En général, les règles Skope sont appliquées pour connaître la cause profonde de chaque problème.
 Comment trouver le nombre de paramètres fournis par le runtime en Java ?
Sep 23, 2023 pm 01:13 PM
Comment trouver le nombre de paramètres fournis par le runtime en Java ?
Sep 23, 2023 pm 01:13 PM
En Java, une façon de transmettre des paramètres au moment de l'exécution consiste à utiliser la ligne de commande ou le terminal. Lors de la récupération de ces valeurs pour les paramètres de ligne de commande, nous devrons peut-être trouver le nombre de paramètres fournis par l'utilisateur au moment de l'exécution, ce qui peut être obtenu à l'aide de l'attribut length. Cet article vise à expliquer le processus de transmission et d'obtention d'un certain nombre de paramètres fournis par l'utilisateur à l'aide d'un exemple de programme. Obtenir le nombre d'arguments fournis par l'utilisateur au moment de l'exécution Avant de trouver le nombre d'arguments de ligne de commande, notre première étape consiste à créer un programme qui permet à l'utilisateur de transmettre des arguments au moment de l'exécution. Paramètre String[] Lors de l'écriture de programmes Java, nous rencontrons souvent la méthode main(). Lorsque la JVM appelle cette méthode, l'application Java commence à s'exécuter. Il est utilisé avec un argument appelé String[]args
 Commande Linux : Comment vérifier le nombre de processus telnet
Mar 01, 2024 am 11:39 AM
Commande Linux : Comment vérifier le nombre de processus telnet
Mar 01, 2024 am 11:39 AM
Les commandes Linux sont l'un des outils indispensables dans le travail quotidien des administrateurs système. Elles peuvent nous aider à accomplir diverses tâches de gestion du système. Lors des travaux d'exploitation et de maintenance, il est parfois nécessaire de vérifier le numéro d'un certain processus dans le système afin de détecter les problèmes et de procéder à des ajustements à temps. Cet article explique comment utiliser les commandes Linux pour vérifier le nombre de processus telnet, apprenons ensemble. Dans les systèmes Linux, nous pouvons utiliser la commande ps combinée avec la commande grep pour afficher le nombre de processus telnet. Tout d'abord, nous devons ouvrir un terminal,
 Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec les mêmes valeurs minimales et maximales
Aug 25, 2023 pm 11:33 PM
Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec les mêmes valeurs minimales et maximales
Aug 25, 2023 pm 11:33 PM
Dans cet article, nous utiliserons C++ pour résoudre le problème de trouver le nombre de sous-tableaux dont les valeurs maximales et minimales sont les mêmes. Voici un exemple du problème −Input:array={2,3,6,6,2,4,4,4}Output:12Explication :{2},{3},{6},{6}, {2 },{4},{4},{4},{6,6},{4,4},{4,4}et{4,4,4}sont les sous-tableaux qui peuvent être formés avec les mêmes éléments maximum et minimum. Entrée : tableau = {3, 3, 1,5,
 Trouver le nombre de façons de parcourir un arbre N-aire en utilisant C++
Sep 04, 2023 pm 05:01 PM
Trouver le nombre de façons de parcourir un arbre N-aire en utilisant C++
Sep 04, 2023 pm 05:01 PM
Étant donné un arbre N-aire, notre tâche est de trouver le nombre total de façons de parcourir l'arbre, par exemple - Pour l'arbre ci-dessus, notre résultat sera de 192. Pour ce problème, nous avons besoin de connaissances en combinatoire. Maintenant, dans ce problème, il nous suffit de vérifier toutes les combinaisons possibles de chaque chemin et cela nous donnera la réponse. Méthode pour trouver la solution Dans cette méthode, il nous suffit d'effectuer un parcours hiérarchique, de vérifier le nombre d'enfants de chaque nœud, puis de le multiplier factoriellement par la réponse. Exemple de code C++ de la méthode ci-dessus #include<bits/stdc++.h>usingnamespacestd;structNode{//s
 Le nombre de triangles isocèles dans un arbre binaire
Sep 05, 2023 am 09:41 AM
Le nombre de triangles isocèles dans un arbre binaire
Sep 05, 2023 am 09:41 AM
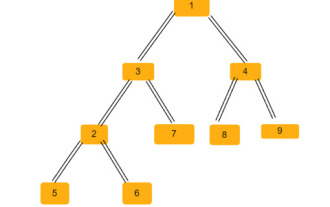
Un arbre binaire est une structure de données dans laquelle chaque nœud peut avoir jusqu'à deux nœuds enfants. Ces enfants sont appelés respectivement enfants de gauche et enfants de droite. Supposons que nous recevions une représentation de tableau parent, vous devez l'utiliser pour créer un arbre binaire. Un arbre binaire peut avoir plusieurs triangles isocèles. Nous devons trouver le nombre total de triangles isocèles possibles dans cet arbre binaire. Dans cet article, nous explorerons plusieurs techniques pour résoudre ce problème en C++. Comprendre le problème vous donne un tableau parent. Vous devez le représenter sous la forme d'un arbre binaire afin que l'index du tableau forme la valeur du nœud de l'arbre et que la valeur dans le tableau donne le nœud parent de cet index particulier. Notez que -1 est toujours le parent racine. Vous trouverez ci-dessous un tableau et sa représentation arborescente binaire. Tableau parental=[0,-1,3,1,
 Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec des sommes impaires
Sep 21, 2023 am 08:45 AM
Écrivez un code en C++ pour trouver le nombre de sous-tableaux avec des sommes impaires
Sep 21, 2023 am 08:45 AM
Un sous-tableau est une partie contiguë d'un tableau. Par exemple, nous considérons un tableau [5,6,7,8], alors il y a dix sous-tableaux non vides, tels que (5), (6), (7), (8), (5,6), (6, 7), (7,8), (5,6,7), (6,7,8) et (5,6,7,8). Dans ce guide, nous expliquerons toutes les informations possibles en C++ pour trouver le nombre de sous-tableaux avec des sommes impaires. Pour trouver le nombre de sous-tableaux de sommes impaires, nous pouvons utiliser différentes méthodes, voici donc un exemple simple - Input:array={9,8,7,6,5}Output:9Explanation:Sumofsubarray-{9}= 9{7





