CMU Zhang Kun : derniers progrès dans la technologie de représentation causale

1. Pourquoi se soucier de la causalité

Tout d'abord, introduisons ce qu'est la causalité :

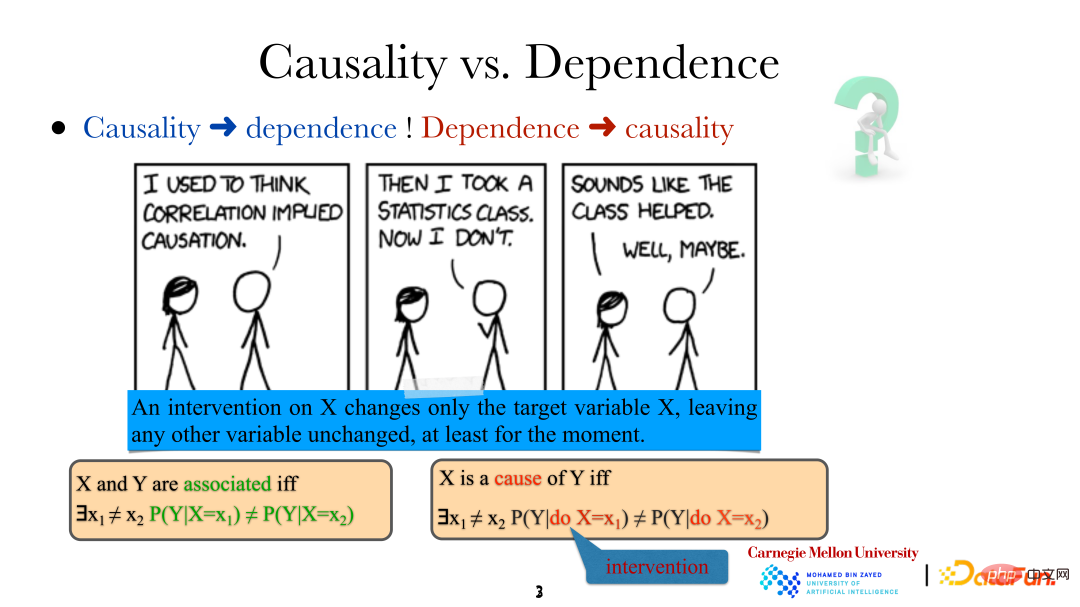
Quand nous disons que les variables/événements sont liés, cela signifie qu'ils ne sont pas indépendants, donc ils ne le sont pas. indépendant. Il doit y avoir une certaine relation. Cependant, la signification de X étant la « cause » de Y est que si une méthode spécifique est utilisée pour changer, ce n'est pas la même chose. Il convient de noter que l'intervention ici n'est pas aléatoire, mais un contrôle direct très précis de la variable cible (changement direct de « il pleut »). Ce changement n'affectera pas directement les autres variables du système. En même temps, de cette manière, c'est-à-dire par intervention humaine directe, nous pouvons également déterminer si une variable est la cause directe d'une autre variable.

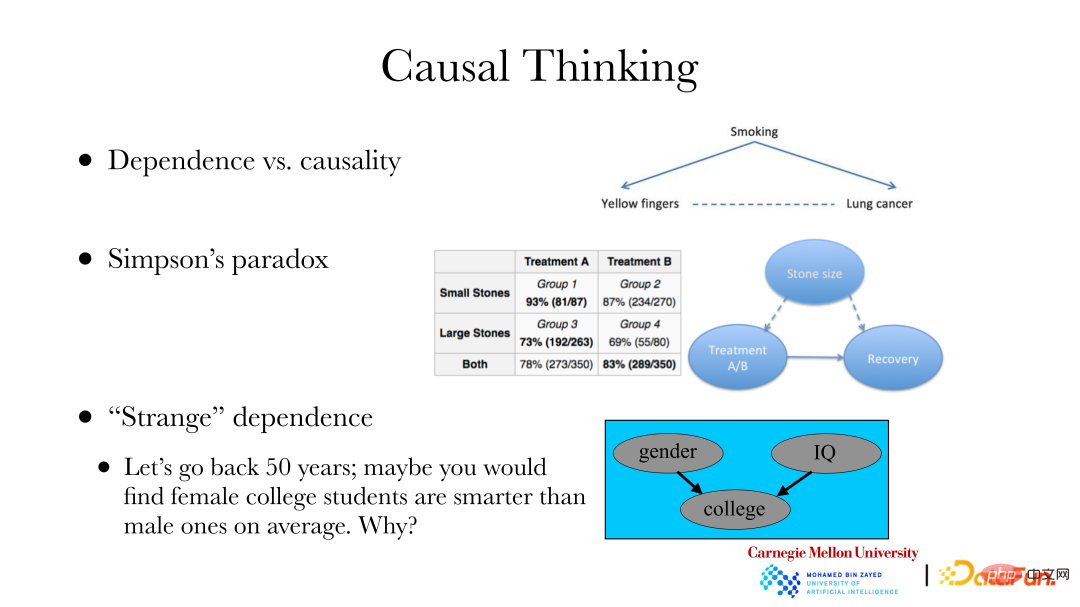
Ce qui suit est un exemple de la nécessité d'analyser la causalité :

① Un cas classique est le suivant : il existe une relation entre les maladies pulmonaires et la couleur des ongles à cause du tabagisme, c'est-à-dire parce que les cigarettes n'ont pas de filtre, c'est le tabagisme régulier. provoquera des dommages aux ongles, le jaunissement, le tabagisme peut également provoquer des maladies pulmonaires. Si vous souhaitez modifier l'incidence d'une maladie pulmonaire dans une certaine zone, elle ne peut pas être améliorée en blanchissant vos ongles. Vous devez trouver la cause de la maladie pulmonaire, plutôt que de modifier la dépendance de la maladie pulmonaire. Pour atteindre l’objectif de modifier l’incidence des maladies pulmonaires, une analyse causale est nécessaire.

② Le deuxième cas est : le paradoxe de Simpson. Le côté droit de l'image ci-dessus est un ensemble de données réel. L'ensemble de données montre deux ensembles de données sur les calculs rénaux, un groupe a des calculs plus petits et l'autre a des calculs plus gros. De plus, il existe deux méthodes de traitement A et B. On peut constater dans le tableau que quel que soit le petit groupe de calculs ou le grand groupe de calculs, les résultats obtenus par la méthode de traitement A sont meilleurs, avec des taux de guérison de 93 % et 73 % respectivement, et les taux de guérison de la méthode de traitement B sont 87% et 69% respectivement. Cependant, lorsque deux groupes de patients atteints de calculs avec la même méthode de traitement étaient mélangés, l'effet global du plan de traitement B (83 %) était meilleur que celui du plan de traitement A (78 %). Supposons que vous soyez un médecin qui ne se soucie que du taux de guérison et de la manière de choisir un plan de traitement pour les nouveaux patients. La raison en est que lorsque nous faisons des recommandations, nous nous soucions uniquement du lien de causalité entre le traitement et la guérison, et ne nous soucions pas des autres dépendances. Cependant, la taille des calculs est une cause fréquente à la fois du traitement et de leur guérison, ce qui entraîne des changements quantitatifs dans la dépendance du traitement et de la guérison. Par conséquent, lorsque nous étudions la relation entre les méthodes de traitement et la guérison, nous devrions discuter de la relation causale entre les premières et les secondes, plutôt que de la relation de dépendance.

③ Troisième cas : il y a 50 ans, les statistiques montraient que les femmes dans les collèges et universités étaient en moyenne plus intelligentes que les hommes, mais en réalité il ne devrait pas y avoir de différence significative. Il existe un biais de sélection, car il est plus difficile pour les femmes que pour les hommes d'entrer à l'université. Autrement dit, lorsque les écoles recrutent des étudiants, celles-ci seront affectées par des facteurs tels que le sexe et la capacité aux examens. Lorsque le « résultat » se produira, il y aura une certaine relation entre le sexe et la capacité à l'examen. Le problème du biais de sélection existe également lors de l’utilisation de données collectées sur Internet. Il existe souvent une relation entre la collecte d'un point de données et certains attributs. Si vous analysez uniquement des données publiées sur Internet, vous devez prêter attention à ces facteurs. Lorsque cela est réalisé, les données comportant un biais de sélection peuvent également être analysées à travers des relations causales, et la nature du groupe tout entier peut alors être restaurée ou déduite.

L'image ci-dessus montre plusieurs problèmes d'apprentissage automatique/deep learning :

① Nous savons qu'il existe une relation entre la meilleure prédiction et la distribution des données. Dans l'apprentissage par transfert, par exemple, si vous souhaitez transférer un modèle de l'Afrique vers les Amériques tout en faisant des prédictions optimales, cela nécessite évidemment des ajustements adaptatifs du modèle en fonction de différentes distributions de données. À l’heure actuelle, il est particulièrement important d’analyser quels changements se sont produits dans la distribution des données et comment ils ont changé. Savoir ce qui a changé dans les données vous permet d'ajuster le modèle en conséquence. Autre exemple, lors de la construction d'un modèle d'IA pour diagnostiquer une maladie, vous ne serez pas satisfait des résultats de diagnostic proposés par la machine. Vous voudrez en outre savoir pourquoi la machine est arrivée à cette conclusion, par exemple quelle mutation a causé la maladie. De plus, la façon de traiter une maladie soulève de nombreuses questions du type « pourquoi ». De même, lorsqu'un système de recommandation fait une recommandation, il voudra savoir pourquoi il recommande cet élément/stratégie, par exemple, l'entreprise souhaite simplement augmenter ses revenus, ou l'élément/la stratégie convient à l'utilisateur, ou l'élément/la stratégie est bénéfique pour l’avenir. Ces questions « pourquoi » sont toutes des questions de cause à effet.

② Dans le domaine du deep learning, il existe la notion d'attaques contradictoires. Comme le montre la figure, si vous ajoutez un bruit spécifique à l'image du panda géant à gauche, ou si vous modifiez des pixels spécifiques, etc., la machine jugera l'image comme d'autres types d'animaux au lieu des pandas géants, et son niveau de confiance est encore très élevé. Cependant, pour les humains, ces deux images sont évidemment des pandas géants. En effet, les fonctionnalités de haut niveau actuellement apprises par les machines à partir d’images ne correspondent pas aux fonctionnalités de haut niveau apprises par les humains. Si les fonctionnalités de haut niveau utilisées par les machines ne correspondent pas à celles des humains, des attaques contradictoires peuvent survenir. Lorsque l'entrée est modifiée, le jugement des humains ou des machines changera et il y aura des problèmes avec le résultat du jugement final. Ce n'est qu'en permettant à la machine d'apprendre des fonctionnalités de haut niveau qui sont cohérentes avec celles des humains, c'est-à-dire qu'elle peut apprendre et utiliser des fonctionnalités de la même manière que les humains, que les attaques contradictoires pourront être évitées.

Pourquoi devons-nous réaliser une représentation causale ?

① Bénéficier des tâches en aval : par exemple, cela peut aider la classification en aval et d'autres tâches à faire mieux.

② Peut expliquer les questions « pourquoi ».

③ Récupérez les véritables caractéristiques causales derrière les données : la métaphysique de Kant en philosophie croit que le monde vécu par les humains est le monde empirique. Bien qu'elle soit basée sur le monde en soi derrière elle, nous ne pouvons pas percevoir directement l'ontologie du monde. Certaines propriétés, telles que le temps, l'espace, l'ordre causal, etc., ont été automatiquement ajoutées au monde expérientiel par le système sensoriel. Par conséquent, si vous souhaitez qu’une machine apprenne des caractéristiques cohérentes avec celles des humains, vous avez besoin qu’elle ait la capacité d’apprendre des caractéristiques telles que l’ordre/la relation causale, le temps et l’espace.

2. Apprentissage des représentations causales : situation indépendante et identiquement distribuée

1. Concepts de base de l'apprentissage des représentations causales

Comment apprendre les relations causales dans la situation indépendante et identiquement distribuée ? Premièrement, il faut répondre à deux questions : premièrement, quelles propriétés des données sont liées à la causalité et quels indices (« empreinte ») se trouvent dans les données. La deuxième question est de savoir si la relation causale peut être retrouvée dans les conditions d’obtention des données, c’est-à-dire la question de l’identifiabilité du système causal.

La propriété la plus essentielle d'un système causal est la « modularité » : bien que les variables du système aient certaines relations, le système peut être divisé en plusieurs sous-systèmes basés sur des relations causales (une cause produit une variable dépendante). Par exemple, « Il pleut », « Le sol est mouillé » et « Le sol est glissant » sont interdépendants et peuvent être divisés en trois sous-systèmes par des relations causales : « Certaines raisons font qu'il pleut », « Il pleut pour provoquer le le sol est mouillé", "Le sol mouillé rend le sol glissant." Bien qu'il existe des dépendances entre les variables, ces trois processus (sous-systèmes) ne sont pas connectés, il n'y a pas de partage de paramètres et les modifications dans un système n'entraîneront pas de modifications dans l'autre système. Par exemple, en pulvérisant certaines substances pour modifier l'effet « sol humide provoquant un sol glissant », cela n'affectera pas s'il pleut ou non, ni l'effet de la pluie sur le sol mouillé. Cette propriété est appelée « modularité », ce qui signifie que le système est divisé en différents sous-modules d'un point de vue causal, et qu'il n'y a aucune connexion entre les sous-modules.

À partir de la modularité, nous pouvons obtenir trois propriétés des systèmes causals :

① Indépendance conditionnelle entre variables.

② Condition sonore indépendante.

③ Changements minimes (et indépendants).

Concernant l'identifiabilité des systèmes causals, d'une manière générale, l'apprentissage automatique lui-même n'accorde pas beaucoup d'attention à la question de l'identifiabilité. Par exemple, le modèle de prédiction doit juger si le résultat de la prédiction est précis ou optimal, mais il n'y a pas de « vérité ». " pour juger. Cependant, l'apprentissage de l'analyse causale et de la représentation causale consiste à restaurer la « vérité » des données, c'est-à-dire qu'il accorde plus d'attention à la question de savoir si la nature causale derrière les données peut être identifiée.

Deux concepts de base sont introduits ci-dessous :

① Découverte causale : explorer la structure/le modèle causal sous-jacent à travers les données.

② Apprentissage de la représentation causale : recherchez les variables cachées de haut niveau sous-jacentes et les relations entre les variables à partir de données directement observées.

2. Division de l'apprentissage des représentations causales

Les méthodes d'apprentissage des représentations causales sont généralement divisées selon les trois perspectives suivantes :

① Propriétés des données : si elles sont indépendantes et identiquement distribuées (« données i.i.d. »). Les données non indépendantes et distribuées de manière identique comprennent des données non indépendantes mais distribuées de manière identique, telles que des données distribuées de manière identique avec une dépendance temporelle (telles que des données de séries chronologiques), ou des données indépendantes mais distribuées différemment, telles que des changements de distribution de données (ou ces deux combinaisons). de ceux-là).

② Contraintes paramétriques (« contraintes paramétriques ») : s'il existe d'autres propriétés supplémentaires sur l'influence de la causalité, comme les modèles paramétriques.

③ Confondeurs potentiels (« confondeurs latents ») : Qu'il s'agisse de permettre l'existence de facteurs communs non observés ou de facteurs confondants dans le système.

La figure suivante montre en détail les résultats spécifiques qui peuvent être obtenus dans différents paramètres :

Par exemple, dans le cas d'une distribution indépendante et identique, s'il n'y a pas de contraintes de modèle de paramètres, qu'il y ait ou non des potentiels des facteurs de confusion, etc. peuvent généralement être obtenus. Classe de Valence (« classe d'équivalence »), s'il existe des contraintes de modèle paramétrique, la vérité derrière elle peut généralement être directement restaurée.

3. Apprentissage de la représentation causale indépendante et identiquement distribuée

La figure ci-dessus montre un exemple sans contraintes de modèle de paramètres dans le cas indépendant et identiquement distribué. Les données montrent un total de 8 variables mesurées pour 250 crânes, notamment le sexe, l'emplacement, la météo ainsi que la taille et la forme du crâne. Les archéologues veulent savoir ce qui cause les différentes apparences des personnes dans différentes régions. Si nous connaissons cette relation causale, nous pourrons peut-être prédire l'apparence des personnes grâce aux changements dans l'environnement et à d'autres facteurs. De toute évidence, l'intervention humaine ne peut pas être effectuée dans de telles conditions. Même si l'intervention est ajoutée, l'observation des résultats prendra beaucoup de temps, de sorte que la relation causale ne peut être trouvée qu'à partir des données d'observation existantes.

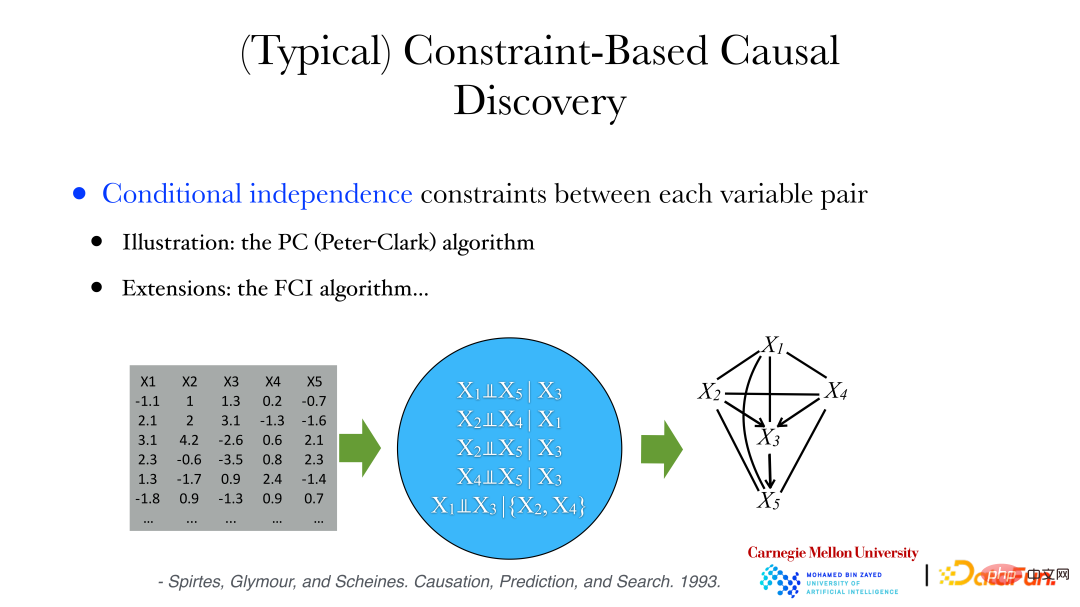
Comme le montre la figure ci-dessus, la relation entre les variables est très complexe, elle peut être linéaire ou non linéaire, et les dimensions des variables peuvent également être incohérentes. Si le sexe est à 1 dimension, les traits du crâne pourraient avoir 255 dimensions. À l’heure actuelle, la propriété d’indépendance conditionnelle peut être utilisée pour construire des relations causales.

Les méthodes incluent les deux suivantes :

① Algorithme PC (Peter-Clark) : L'algorithme suppose qu'aucun facteur commun n'est observé dans le système.

② Algorithme FCI : utilisé lorsqu'il y a des variables cachées.

Ce qui suit utilisera l'algorithme PC pour analyser les données archéologiques : une série de propriétés conditionnellement indépendantes peuvent être dérivées des données, telles que les variables X1 et X5 étant conditionnellement indépendantes lorsque X3 est donné, etc. En même temps, nous pouvons prouver que si deux variables sont conditionnellement indépendantes, alors il n’y a aucune arête entre elles. Ensuite, nous pouvons partir du graphe complet. Si les variables sont conditionnellement indépendantes, supprimez les arêtes connectées pour obtenir un graphe non orienté. Ensuite, jugez la direction des arêtes dans le graphe pour trouver le graphe acyclique orienté (DAG, Directed Acyclic. Graph) ou une collection de graphiques acycliques orientés pour satisfaire les contraintes d'indépendance conditionnelle entre les variables des données.

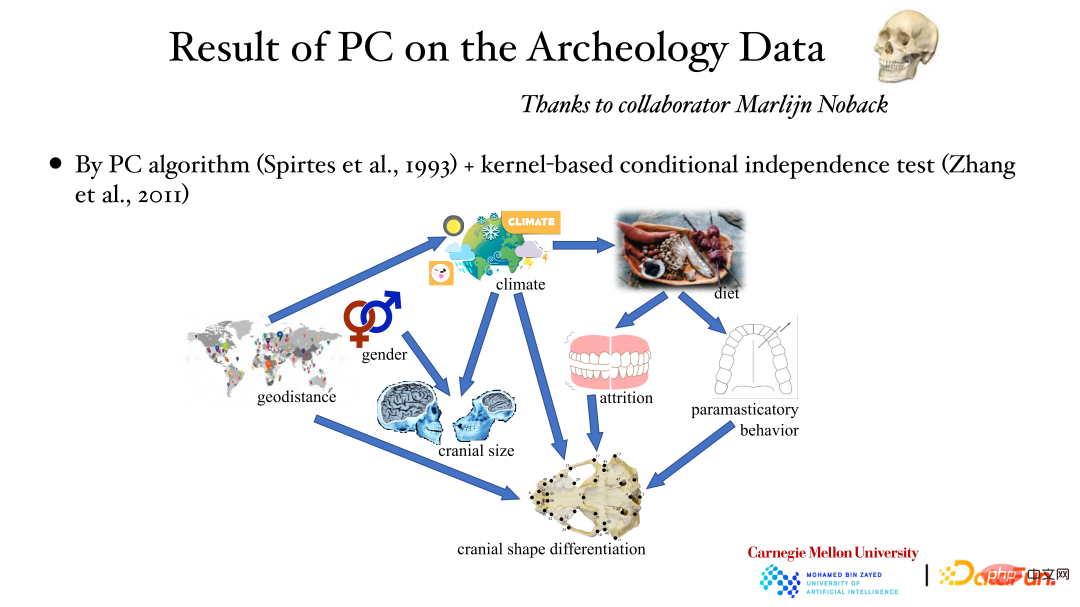
La figure ci-dessus montre les résultats de l'analyse des données archéologiques à l'aide de l'algorithme PC et de la méthode de test d'indépendance conditionnelle du noyau : l'emplacement géographique affecte la météo, la météo affecte la taille du crâne et le sexe affecte également la taille du crâne, etc. La relation causale derrière cela a été obtenue grâce à l’analyse des données.

Parmi les deux problèmes que nous venons d'évoquer, l'un est de trouver la direction de chaque arête de la variable DAG, ce qui nécessite des hypothèses supplémentaires. Si vous faites des hypothèses sur la manière dont la cause affecte l'effet, vous constaterez que la cause et l'effet sont asymétriques, vous pourrez donc découvrir la direction de la cause et de l'effet. L'arrière-plan des données dans la figure ci-dessous est toujours constitué de données indépendantes et distribuées de manière identique, et des restrictions de paramètres supplémentaires ont été ajoutées, et les facteurs de confusion ne sont toujours pas autorisés dans le système. À l'heure actuelle, les trois types de modèles suivants peuvent être utilisés pour étudier la direction de la causalité :

① Modèle linéaire non gaussien

② Modèle causal post-non-linéaire (PNL, Modèle causal post-non-linéaire) ; Modèle de bruit additif (ANM, Additive noise model).

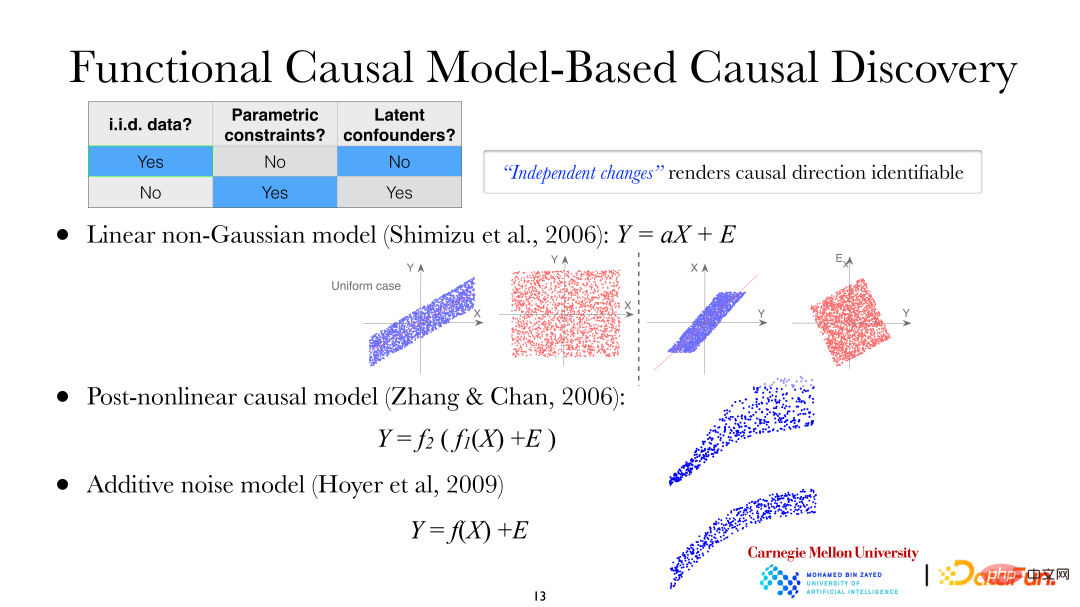Dans le modèle linéaire non gaussien, on suppose que X mène à Y, c'est-à-dire que X est la variable dépendante et Y est la variable d'effet. On peut voir sur la figure que lorsqu'on utilise X pour expliquer Y pour une régression linéaire, les résidus et X sont indépendants mais à l'inverse, lorsqu'on utilise Y pour expliquer, ils ne sont évidemment pas indépendants (dans le cas d'une gaussienne linéaire, la non-corrélation entre les variables signifie indépendance. Mais pour le moment, le modèle est linéaire non gaussien, c'est-à-dire non corrélé ne signifie pas qu'ils sont indépendants). On constate qu’il existe une asymétrie entre la variable dépendante et la variable d’effet. Il en va de même pour les modèles causals post-non linéaires et les modèles de bruit additif.

La figure ci-dessus montre le modèle causal post-non linéaire : la deuxième fonction non linéaire (f2) à l'extérieur est généralement utilisée pour décrire les changements non linéaires introduits pendant le processus de mesure dans le système, souvent lors de l'observation/mesure de données. Il n'y aura pas de changement non linéaire. -changements linéaires. Par exemple, dans le domaine biologique, des changements non linéaires supplémentaires se produiront lors de l’utilisation d’instruments pour mesurer les données d’expression génétique. Les modèles linéaires, les modèles de bruit additifs non linéaires et les modèles de bruit multiplicatifs sont tous des cas particuliers des modèles PNL.

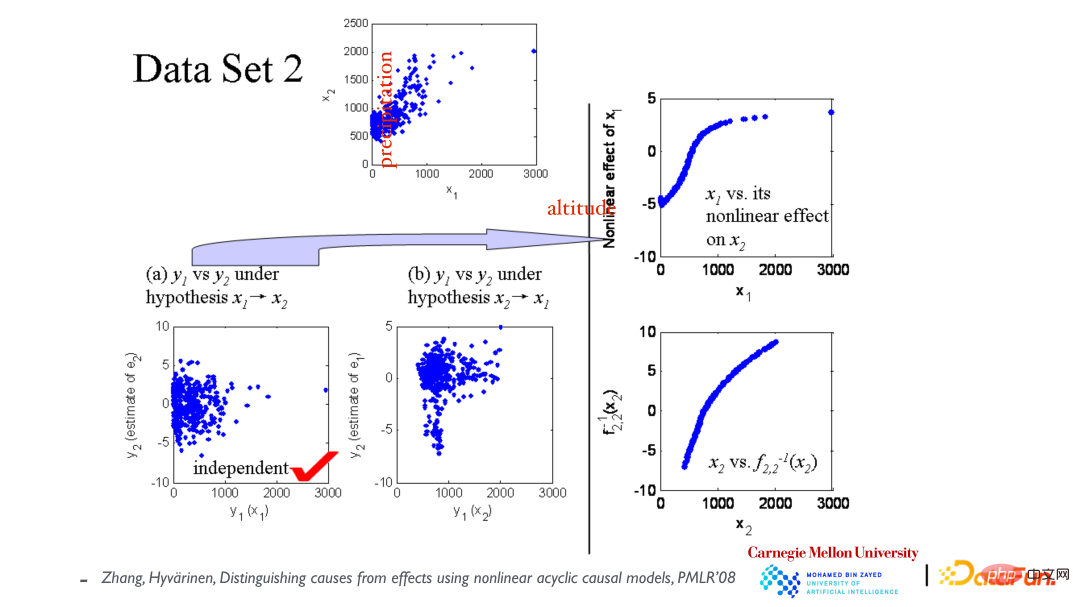Le nuage de points du haut montre la relation entre les variables x1 (altitude) et x2 (précipitations annuelles). Supposons d'abord que x1 provoque x2, puis construisons un modèle pour ajuster les données. Comme indiqué dans le coin inférieur gauche, les résidus et x1 sont indépendants ; supposons ensuite que x2 provoque x1 et ajustons à nouveau le modèle. et x2 ne sont pas indépendants (voir photo du milieu). De là, on conclut que la direction causale est causée par x1 menant à x2.

L'asymétrie de la variable causale peut effectivement être retrouvée à partir de l'exemple précédent, mais ce résultat peut-il être garanti théoriquement ? Et c'est le seul résultat correct. La direction opposée (effet à cause) ne peut pas expliquer les données ? La preuve est celle présentée dans le tableau ci-dessus. Dans cinq cas, les données peuvent être expliquées dans les deux sens (cause à effet, effet à cause). Ces cinq cas sont très particuliers. Le premier est le modèle gaussien linéaire, où la relation est linéaire et la distribution est gaussienne, où l'asymétrie causale disparaît. Les quatre autres sont des modèles spéciaux.

Même si les données sont analysées à l'aide d'un modèle post-non linéaire, la cause et l'effet peuvent être distingués. Des résidus indépendants peuvent être trouvés dans la bonne direction, mais pas dans la direction opposée. Étant donné que le modèle linéaire et le modèle de bruit additif non linéaire sont tous deux des cas particuliers du modèle post-non linéaire, les deux modèles sont également applicables dans ce cas et peuvent trouver la direction causale.

Étant donné deux variables, leurs directions causales peuvent être trouvées grâce à la méthode ci-dessus. Mais dans la plupart des cas, les problèmes suivants doivent être résolus : Par exemple, dans le domaine de la psychologie, les réponses à certaines questions (xi) sont collectées au moyen de questionnaires. Il existe une dépendance entre ces réponses, et on ne considère pas qu'il y en ait une. une relation entre ces réponses.

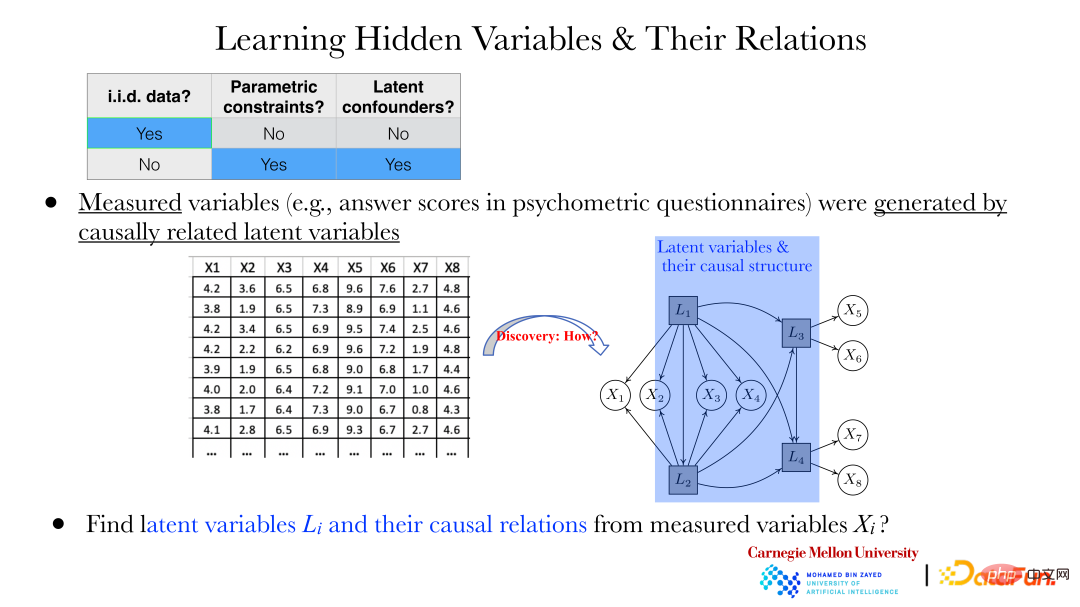
Mais comme le montre la figure ci-dessus, ces xi sont générés par les variables cachées Li derrière eux. Comment révéler les variables cachées Li et la relation entre les variables cachées à travers les xi observés est particulièrement important.

Ces dernières années, certaines méthodes peuvent nous aider à trouver ces variables dépendantes et leurs relations. La figure ci-dessus montre un exemple d'application de la méthode GIN (Generalized Independent Noise), qui peut résoudre une série de problèmes. Le contenu des données est l’épuisement professionnel des enseignants, qui contient 28 variables. L'image de droite montre les variables cachées possibles qui, proposées par les experts, pourraient conduire à ces conditions d'épuisement professionnel (variables observées), ainsi que la relation entre les variables cachées. Les résultats obtenus en analysant les données observées par la méthode GIN sont cohérents avec les résultats donnés par les experts. Les experts effectuent des analyses grâce à des connaissances de base qualitatives, et la méthode d'analyse quantitative des données fournit une vérification et un soutien aux résultats des experts.

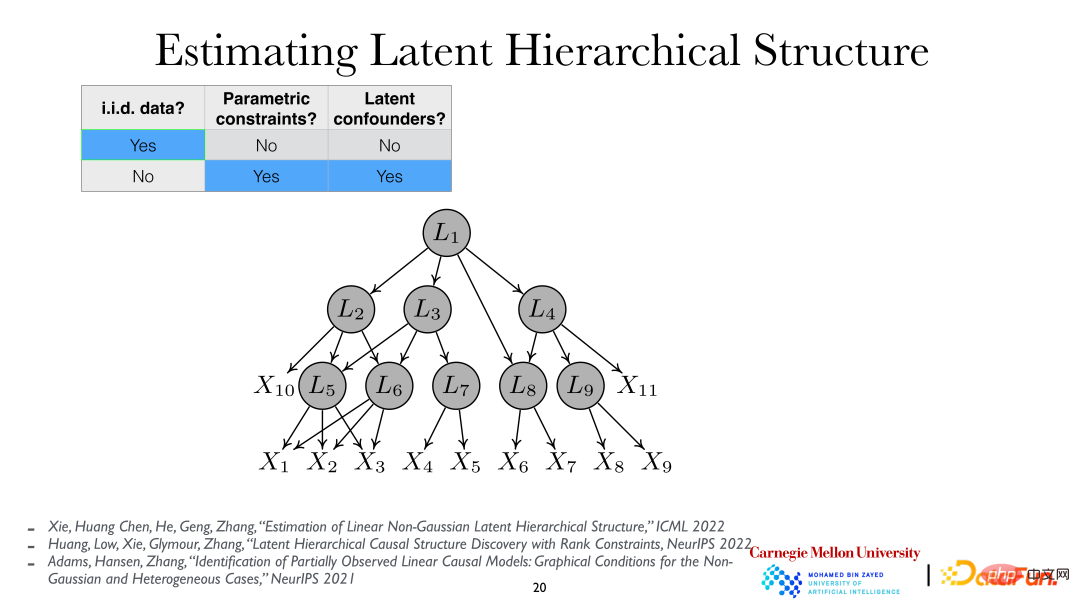
Pour une analyse plus approfondie, on peut supposer que les variables latentes sont hiérarchiques, c'est-à-dire la structure hiérarchique des variables latentes (Latent Hierarchical Structure). En analysant les variables observées xi, les variables cachées Li et leurs relations derrière elles peuvent être révélées.

3. Apprentissage de la représentation causale à partir de séries chronologiques

Maintenant que nous comprenons la méthode de représentation causale dans la situation indépendante et identiquement distribuée, nous allons ensuite présenter comment trouver les variables cachées et la causalité derrière elles dans des conditions non linéaires et indépendantes et identiquement distribuées. situation. D'une manière générale, dans le cas d'une distribution indépendante et identique, des conditions relativement fortes (y compris des hypothèses de modèles paramétriques, des modèles linéaires, des graphiques clairsemés, etc.) sont nécessaires pour trouver la relation causale. Dans d’autres cas, la causalité peut être trouvée plus facilement.

Ce qui suit présentera comment trouver des représentations causales à partir de séries chronologiques, c'est-à-dire comment effectuer une analyse causale lorsque les données ne sont pas indépendantes mais distribuées de manière identique :

Si la relation causale se produit dans le temps observé séries Il s'agit d'un problème classique consistant à trouver la causalité à partir de données de séries chronologiques, c'est-à-dire la causalité de Granger. La causalité de Granger est cohérente avec la causalité mentionnée précédemment basée sur l'indépendance conditionnelle, mais avec l'ajout de contraintes de temps (si elle ne peut pas survenir plus tôt que la cause), et de plus, des relations causales instantanées peuvent être introduites.

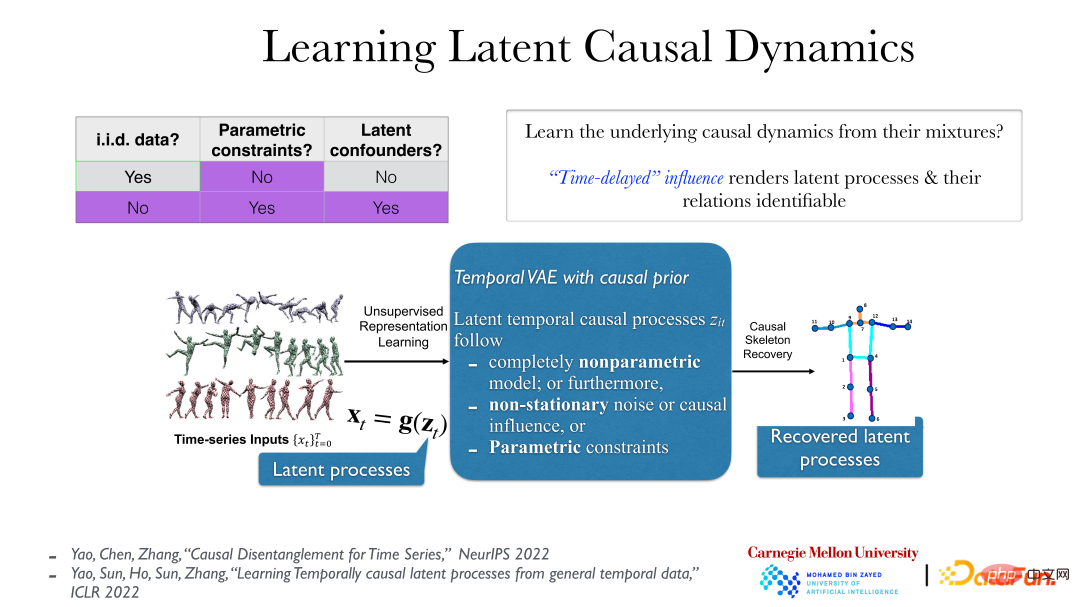
La photo ci-dessus montre une méthode plus pratique. Dans les données vidéo, le processus latent véritablement significatif derrière les données est que les données que nous observons, comme leur reflet, sont générées par leur transformation par une fonction non linéaire lisse et réversible. Le véritable processus causal implicite a généralement un lien causal dans le temps, tel que « pousser puis tomber ». Cet effet causal est généralement retardé. Dans ces conditions, même sous des hypothèses très faibles (même si le processus latent sous-jacent est non paramétrique et que la fonction g (du processus latent à la série temporelle observée) est également non paramétrique), le processus latent sous-jacent peut être complètement compris. Tout est révélé.

En effet, après être revenu au processus implicite réel, il n'y a pas de causalité ni de dépendance instantanées, et la relation entre les objets sera plus claire. Cependant, si vous utilisez la mauvaise méthode d'analyse pour examiner les données d'observation, par exemple en observant directement les pixels des données vidéo, vous constaterez qu'il existe une dépendance instantanée entre eux.

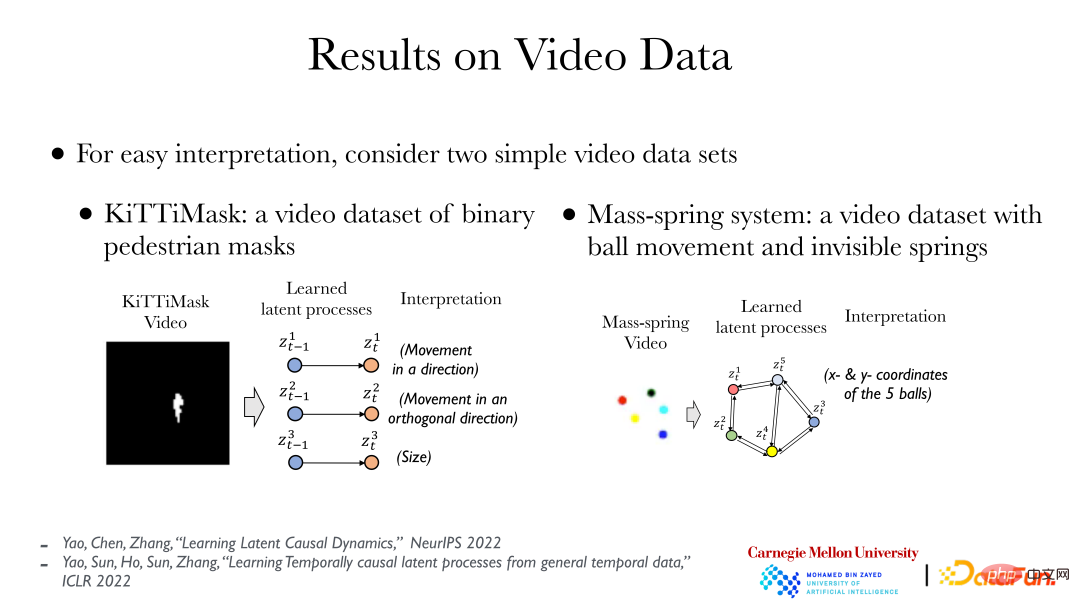
L'image ci-dessus montre deux cas simples : le côté gauche montre les données vidéo KiTTiMask. L'analyse des données vidéo montre trois processus cachés : le déplacement dans une direction ; le déplacement dans la direction verticale et la modification de la taille du masque. Le côté droit montre 5 petites boules de couleurs différentes. Certaines boules sont reliées par des ressorts (invisibles). Grâce à l'analyse, 10 variables cachées (coordonnées x, y des 5 petites boules) peuvent être obtenues, puis la cause et l'effet entre elles. on peut trouver des relations (il y a des ressorts entre certaines boules). Sur la base de données vidéo, nous pouvons utiliser directement une méthode totalement non supervisée et introduire le principe de cause à effet pour trouver la relation entre les objets qui se cachent derrière.

4. Apprentissage de la représentation causale sous plusieurs distributions

Enfin, introduisons l'analyse causale lorsque la distribution des données change :

Lors de l'enregistrement des variables/processus au fil du temps, on constate souvent que la distribution des données change avec le temps. Cela est dû à un changement dans la valeur de la variable sous-jacente non observée/mesurée, la distribution des données de la variable observée change en réponse. De même, si vous mesurez des données dans différentes conditions, vous constaterez que la distribution des données mesurées dans différentes conditions/emplacements peut également être différente.

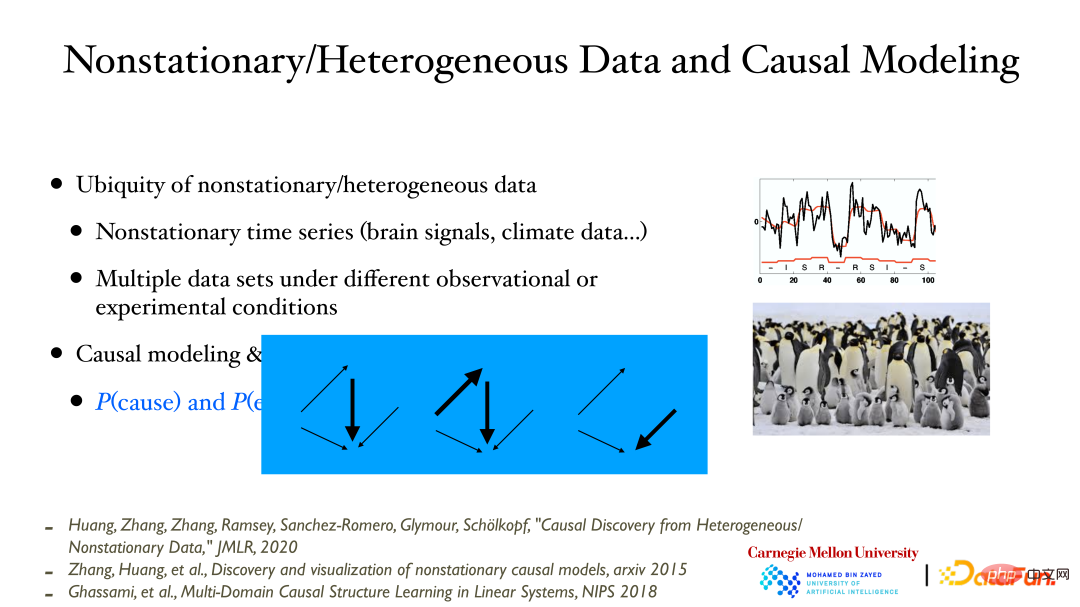
Le point à souligner ici est qu'il existe un lien très étroit entre la modélisation causale et les changements dans la distribution des données. Lorsqu'un modèle causal est donné, basé sur la nature modulaire, ces sous-modules peuvent changer indépendamment. Si ce changement peut être observé à partir des données, l'exactitude du modèle causal peut être vérifiée. Le changement du modèle causal évoqué ici signifie que l’influence causale peut devenir plus forte/faible, voire disparaître.

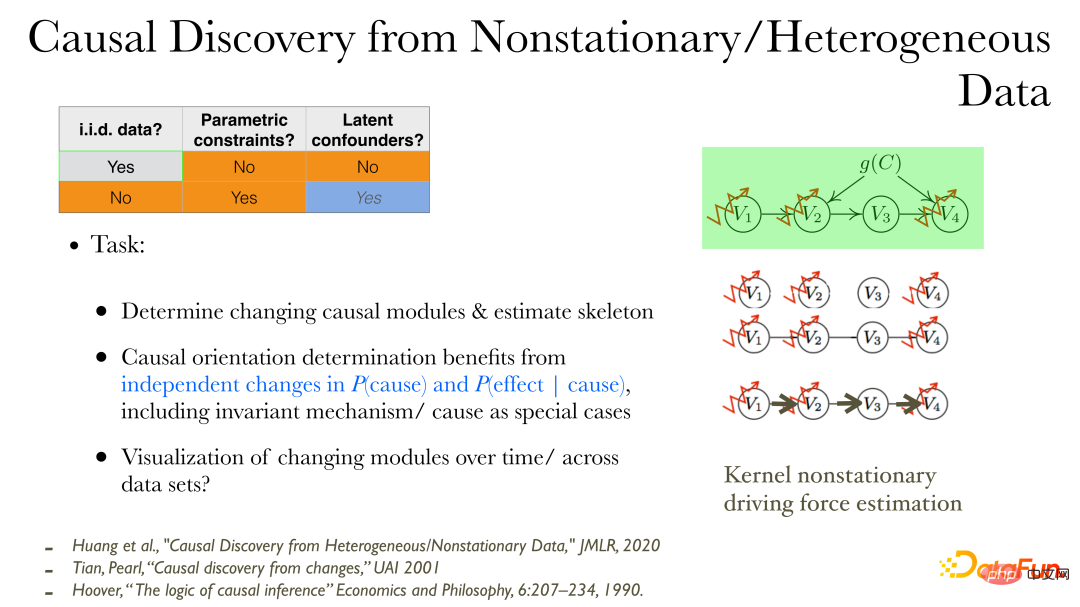
Dans les données non stationnaires/hétérogènes, les relations causales peuvent être découvertes plus directement une fois que les variables observées sont données :

① Tout d'abord, vous pouvez observer le processus de production causal des variables qui changeront ; bord non orienté (squelette) de l'influence causale ;

③ Trouver la direction de la causalité : lorsque la distribution des données change, des propriétés supplémentaires peuvent être utilisées : les changements dans la cause et les changements dans l'effet en fonction de la cause sont indépendants les uns des autres et ont aucune connexion. Parce que les changements entre les différents modules sont indépendants ;

④ Utiliser des méthodes de visualisation de faible dimension pour décrire le processus de changements causals.

La figure suivante montre quelques résultats de l'analyse des données de rendement quotidien des actions (données instantanées, sans décalage temporel) à la Bourse de New York :

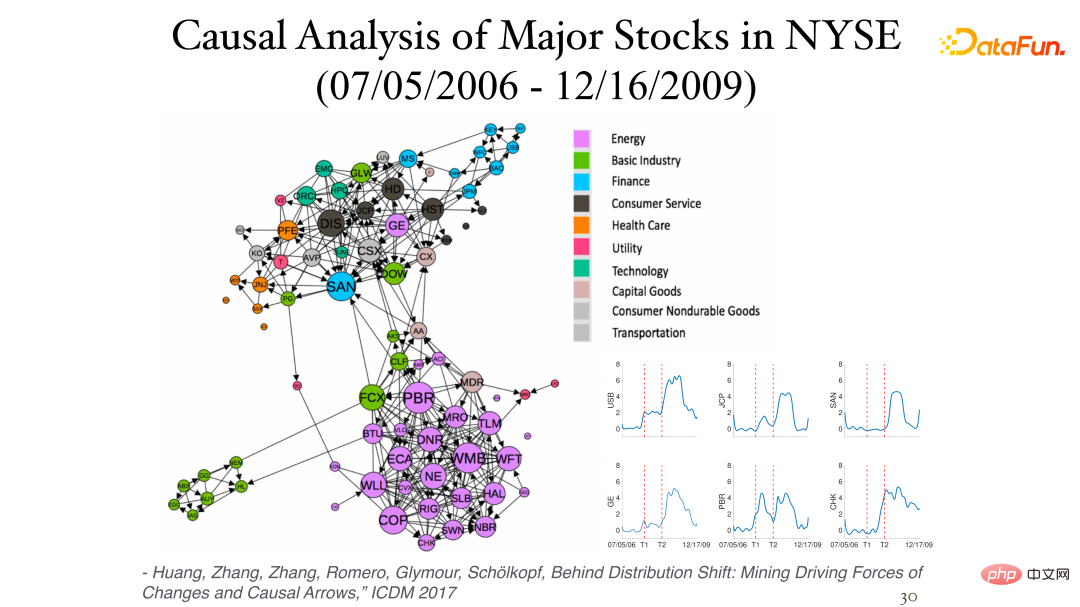L'asymétrie entre elles peut être trouvée grâce à l'influence de non-stationnarité. Différents secteurs appartiennent souvent à la même catégorie (cluster) et sont étroitement liés. L'image dans le coin inférieur droit montre le processus causal des variations des stocks au fil du temps, les deux axes verticaux représentant respectivement les crises financières de 2007 et 2008.

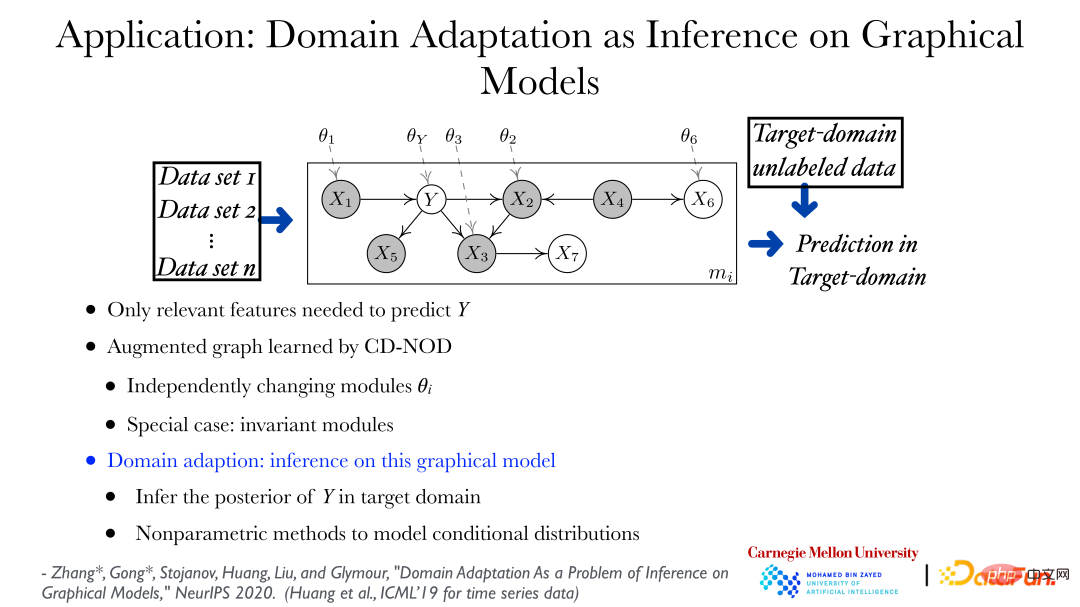Grâce à la méthode d'analyse causale dans des conditions multi-distributions, les modèles de changement de données peuvent être trouvés à partir de différents ensembles de données, et une application directe peut être utilisée pour l'apprentissage par transfert et l'adaptation de domaine. Comme le montre la figure ci-dessus, vous pouvez découvrir les règles changeantes des données de différents ensembles de données et utiliser un graphique augmenté pour montrer comment la distribution des données peut changer. Dans la figure, theta_Y représente, Y lui donne la distribution sous. le nœud parent peut changer en fonction de son domaine. Sur la base du graphique décrivant les changements dans la distribution des données, prédire Y dans un nouveau champ ou champ cible est un problème très standard, c'est-à-dire que trouver la probabilité a posteriori de Y étant donné la valeur de la caractéristique est un problème d'inférence.

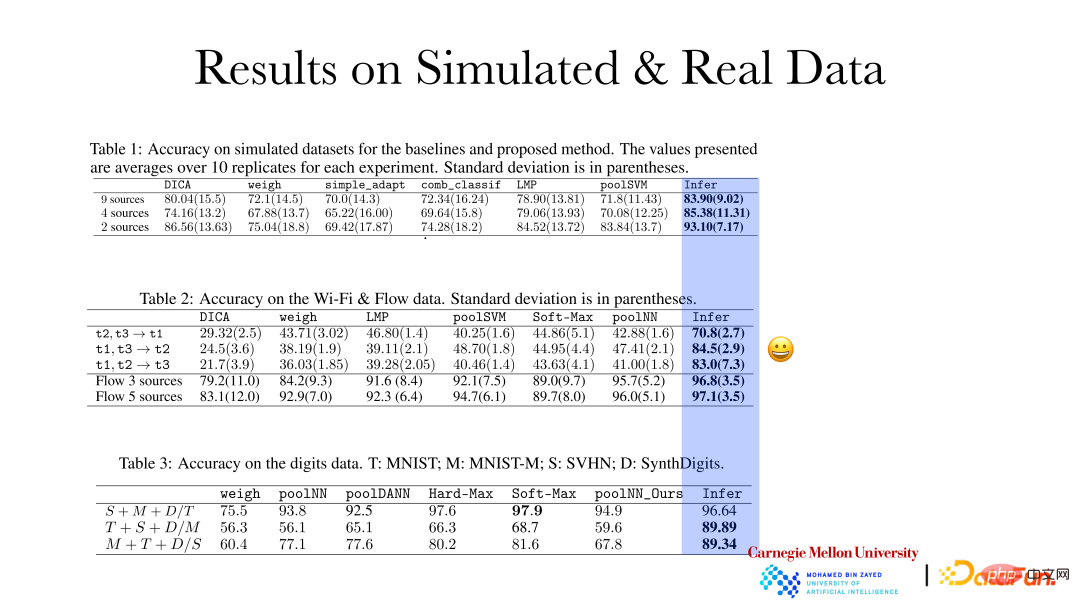La figure ci-dessus montre que la précision de l'effet de raisonnement de la méthode de représentation causale sur les données simulées et les données réelles a été considérablement améliorée. Sur la base des règles de changement qualitatif et de la variabilité des différents champs, des ajustements adaptatifs seront effectués lorsque de nouveaux champs émergeront. Ce type d'effet de prédiction sera meilleur.

La figure ci-dessus montre des travaux récents liés au désenchevêtrement partiel pour l'adaptation de domaine. Compte tenu de la fonctionnalité et de la cible, supposons que tout est non paramétrique et que certains facteurs ne changent pas avec le domaine, c'est-à-dire que la distribution est stable, mais certains facteurs peuvent changer. J'espère trouver ces très rares facteurs qui modifient la distribution. Sur la base des facteurs trouvés, différents domaines peuvent être alignés ensemble, puis les relations correspondantes entre différents domaines peuvent être trouvées, de sorte que l'apprentissage par adaptation/transfert de domaine soit une évidence. Il peut être prouvé que les facteurs indépendants à l'origine des changements dans la distribution peuvent être directement récupérés à partir des données d'observation et que les facteurs inchangés peuvent restaurer leur sous-espace. Comme le montre le tableau, les méthodes ci-dessus peuvent obtenir de bons résultats en matière d'adaptation de domaine. Dans le même temps, cette méthode est également conforme au principe de changement minimal, c'est-à-dire que l'on espère que les facteurs les moins modifiés pourront être utilisés pour expliquer comment les facteurs de données dans différents domaines ont changé, afin de leur correspondre.

Pour résumer, ce partage comprend principalement le contenu suivant :

① Une série de problèmes d'apprentissage automatique nécessitent une représentation appropriée des données qui se cachent derrière. Par exemple, lorsque vous prenez une décision, vous souhaitez connaître l'impact de la décision, afin de pouvoir prendre la décision optimale ; en matière d'adaptation/généralisation de domaine, vous souhaitez savoir comment la distribution des données a changé, afin de prendre une décision. la prédiction optimale ; dans l'apprentissage par renforcement, l'interaction de l'agent avec l'environnement et la récompense apportée par l'interaction elle-même sont un problème causal ; le système de recommandation est également un problème causal, car l'utilisateur est une IA digne de confiance, une IA explicable ; l’équité sont toutes liées à la représentation causale.

② La causalité, y compris les variables cachées, peut être entièrement récupérée à partir des données sous certaines conditions. Vous pouvez vraiment comprendre la nature du processus qui se cache derrière grâce aux données, puis les utiliser.

③ La causalité n'est pas un mystère. Tant qu’il existe des données et que l’hypothèse est appropriée, la causalité sous-jacente peut être trouvée. Les hypothèses formulées ici devraient de préférence être testables.

En général, l'apprentissage de la représentation causale a de grandes perspectives d'application. Dans le même temps, de nombreuses méthodes doivent être développées de toute urgence et nécessitent des efforts conjoints de tous.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!