Pour résoudre le problème de l'apprentissage des représentations VAE, l'Université d'Hokkaido a proposé un nouveau modèle génératif GWAE

L'apprentissage de représentations de faible dimension de données de grande dimension est une tâche fondamentale dans l'apprentissage non supervisé, car de telles représentations capturent succinctement l'essence des données et permettent d'effectuer des tâches en aval basées sur des entrées de faible dimension. L'auto-encodeur variationnel (VAE) est une méthode d'apprentissage de représentation importante, mais en raison de son contrôle objectif, l'apprentissage de la représentation reste une tâche difficile. Bien que l'objectif de limite inférieure de preuve (ELBO) de la VAE soit modélisé de manière générative, l'apprentissage des représentations n'est pas directement ciblé sur cet objectif, ce qui nécessite des modifications spécifiques à la tâche d'apprentissage des représentations, telles que le démêlage. Ces modifications conduisent parfois à des changements implicites et indésirables dans le modèle, ce qui rend l'apprentissage de la représentation contrôlée une tâche difficile.

Pour résoudre le problème d'apprentissage des représentations dans les auto-encodeurs variationnels, cet article propose un nouveau modèle génératif appelé Gromov-Wasserstein Autoencoders (GWAE). GWAE fournit un nouveau cadre pour l'apprentissage des représentations basé sur l'architecture du modèle d'encodeur automatique variationnel (VAE). Contrairement aux méthodes traditionnelles d'apprentissage des représentations basées sur la VAE pour la modélisation générative des variables de données, GWAE obtient des représentations bénéfiques grâce à un transfert optimal entre les données et les variables latentes. La métrique de Gromov-Wasserstein (GW) rend possible ce transfert optimal entre variables non comparables (par exemple des variables de dimensions différentes), qui se concentre sur la structure de distance des variables considérées. En remplaçant l'objectif ELBO par la métrique GW, GWAE effectue une comparaison entre les données et l'espace latent, ciblant directement l'apprentissage des représentations dans les auto-encodeurs variationnels (Figure 1). Cette formulation de l'apprentissage des représentations permet aux représentations apprises d'avoir des propriétés spécifiques considérées comme bénéfiques (par exemple, la décomposabilité), appelées méta-priorités.

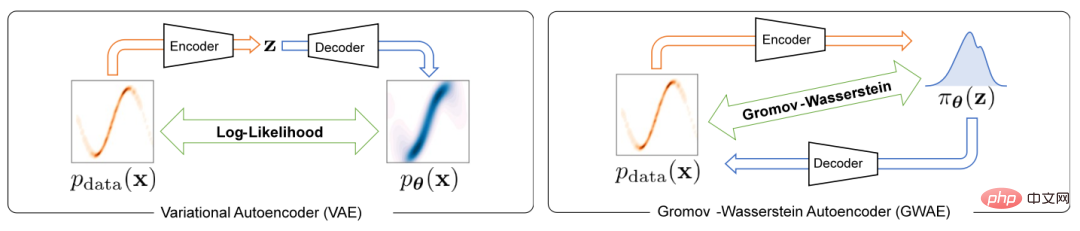
Figure 1 La différence entre VAE et GWAE

Cette recherche a été acceptée par l'ICLR 2023.

• Lien papier : https://arxiv.org/abs/2209.07007
• ​Lien code : https://github.com/ganmodokix/gwae

Introduction à la méthode

La cible GW entre la distribution des données et la distribution a priori potentielle est définie comme suit :

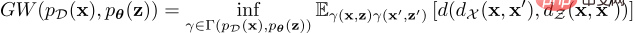
Cette formule de coût de transmission optimal peut mesurer l'incohérence des distributions dans des espaces incomparables cependant, pour des distributions continues, en raison de la ; nécessité Tous les couplages ont une limite inférieure et il n'est pas pratique de calculer les valeurs exactes de GW. Pour résoudre ce problème, GWAE résout un problème d'optimisation détendu pour estimer et minimiser l'estimateur GW, dont le gradient peut être calculé par différenciation automatique. L'objectif de relaxation est la somme de la métrique GW estimée et de trois pertes de régularisation, qui peuvent toutes être implémentées dans un cadre de programmation différenciable tel que PyTorch. Cet objectif de relaxation se compose d'une perte principale et de trois pertes de régularisation, à savoir la perte principale estimée de GW, la perte de reconstruction basée sur WAE, la perte de condition suffisante fusionnée et la perte de régularisation d'entropie.

Ce schéma peut également personnaliser de manière flexible la distribution antérieure pour introduire des fonctionnalités bénéfiques dans la représentation de faible dimension. Plus précisément, cet article présente trois populations antérieures, à savoir :

Neural Prior (NP) Dans les GWAE avec NP, un réseau neuronal entièrement connecté est utilisé pour construire un dispositif d'échantillonnage préalable. Cette famille de distributions a priori fait moins d'hypothèses sur les variables sous-jacentes et convient aux situations générales.

Factorized Neural Prior (FNP) Dans les GWAE avec FNP, un échantillonneur est construit à l'aide d'un réseau neuronal connecté localement, où les entrées pour chaque variable latente sont générées indépendamment. Cet échantillonneur produit une représentation factorisée a priori et une représentation indépendante par terme, ce qui constitue une méthode importante pour le démêlage méta-a priori représentatif.

Gaussian Mixture Prior (GMP) Dans GMP, il est défini comme un mélange de plusieurs distributions gaussiennes, et son échantillonneur peut être implémenté à l'aide de techniques de paramétrage lourdes et de techniques Gumbel-Max. GMP permet de faire l'hypothèse de clusters dans la représentation, où chaque composante gaussienne du prior est censée capturer un cluster.

Expériences et résultats

Cette étude évalue empiriquement GWAE avec deux méta-prieurs principaux : désentremêlement et clustering.

Démêlement L'étude a utilisé l'ensemble de données 3D Shapes et la métrique DCI pour mesurer la capacité de démêlage de GWAE. Les résultats montrent que GWAE utilisant FNP est capable d'apprendre les facteurs de teinte des objets sur un seul axe, ce qui démontre la capacité de démêlage de GWAE. L'évaluation quantitative démontre également les performances de démêlage du GWAE.

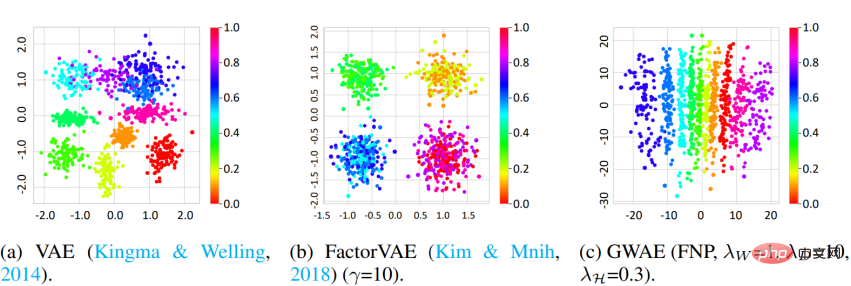
Clustering Pour évaluer les représentations obtenues sur la base des méta-priorités de clustering, cette étude a mené une détection hors distribution (OoD). L'ensemble de données MNIST est utilisé comme données In-Distribution (ID) et l'ensemble de données Omniglot est utilisé comme données OoD. Alors que MNIST contient des chiffres manuscrits, Omniglot contient des lettres manuscrites avec des lettres différentes. Dans cette expérience, les ensembles de données ID et OoD partagent le domaine des images manuscrites, mais ils contiennent des caractères différents. Les modèles sont formés sur les données d'identification, puis utilisent leurs représentations apprises pour détecter les données d'identification ou OoD. Dans VAE et DAGMM, la variable utilisée pour la détection OoD est le log-vraisemblance a priori, tandis que dans GWAE, c'est le potentiel de Kantorovich. Le prior pour GWAE a été construit en utilisant GMP pour capturer les clusters de MNIST. La courbe ROC montre les performances de détection OoD des modèles, les trois modèles atteignant des performances presque parfaites. Cependant, le GWAE construit à l'aide de GMP a obtenu les meilleurs résultats en termes d'aire sous la courbe (AUC).

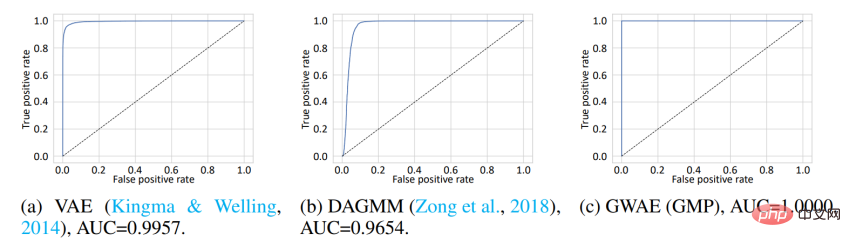
De plus, cette étude a évalué la capacité générative du GWAE.

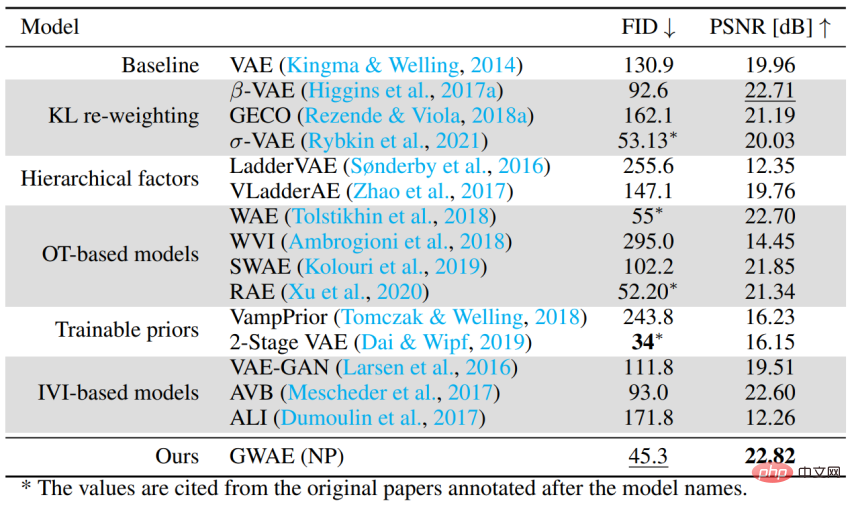
Performances en tant que modèle génératif basé sur un auto-encodeur Pour évaluer la capacité de GWAE à gérer le cas général sans méta-prieurs spécifiques, les performances génératives ont été évaluées à l'aide de l'ensemble de données CelebA. L'expérience utilise FID pour évaluer les performances génératives du modèle et PSNR pour évaluer les performances d'auto-encodage. GWAE a obtenu la deuxième meilleure performance générative et la meilleure performance d'auto-encodage en utilisant NP, démontrant sa capacité à capturer la distribution des données dans son modèle et à capturer les informations sur les données dans sa représentation.

Résumé

• GWAE est un modèle génératif d'auto-encodeur variationnel construit sur la base de la métrique de Gromov-Wasserstein et est conçu pour effectuer directement un apprentissage de représentation.
• Étant donné que l'a priori ne nécessite que des échantillons différenciables, divers paramètres de distribution a priori peuvent être construits pour supposer des méta-a priori (propriétés idéales de la représentation).
• Des expériences sur les méta-prieurs primaires et l'évaluation des performances en tant qu'auto-encodeur variationnel démontrent la flexibilité de la formulation GWAE et les capacités d'apprentissage des représentations de GWAE.
• Page d'accueil personnelle du premier auteur Nao Nakagawa : https://ganmodokix.com/note/cv
• Page d'accueil du Laboratoire multimédia de l'Université d'Hokkaido : https://www-lmd.ist.hokudai ac.jp. /

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!