 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Résumé des points de connaissances importants liés aux modèles de régression d'apprentissage automatique
Résumé des points de connaissances importants liés aux modèles de régression d'apprentissage automatique
Résumé des points de connaissances importants liés aux modèles de régression d'apprentissage automatique
1. Quelles sont les hypothèses de la régression linéaire ?
La régression linéaire repose sur quatre hypothèses :
- Linéarité : il doit y avoir une relation linéaire entre la variable indépendante (x) et la variable dépendante (y), ce qui signifie qu'un changement dans la valeur x doit également modifier la valeur y dans la même direction.
- Indépendance : les entités doivent être indépendantes les unes des autres, ce qui signifie une multicolinéarité minimale.
- Normalité : Les résidus doivent être normalement répartis.
- Homoscédasticité : la variance des points de données autour de la ligne de régression doit être la même pour toutes les valeurs.
2. Qu'est-ce qu'un résidu et comment est-il utilisé pour évaluer les modèles de régression ?
L'erreur résiduelle fait référence à l'erreur entre la valeur prédite et la valeur observée. Il mesure la distance entre les points de données et la ligne de régression. Il est calculé en soustrayant les valeurs prédites des valeurs observées.
Les tracés résiduels sont un excellent moyen d'évaluer les modèles de régression. C'est un graphique qui montre tous les résidus sur l'axe vertical et les caractéristiques sur l'axe des x. Si les points de données sont dispersés de manière aléatoire sur des lignes sans motif, alors un modèle de régression linéaire s'adapte bien aux données, sinon nous devrions utiliser un modèle non linéaire.
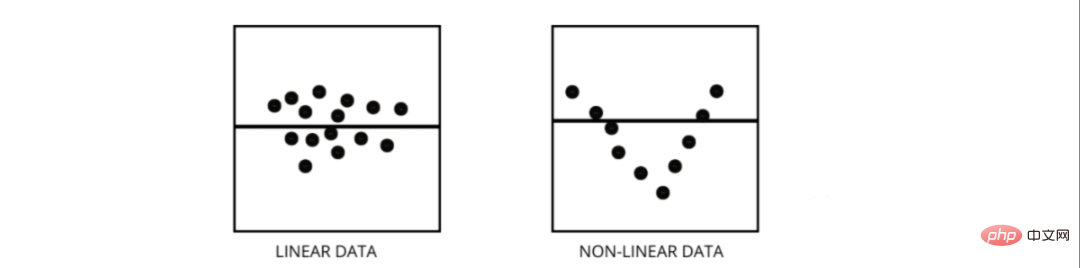
3. Comment faire la distinction entre un modèle de régression linéaire et un modèle de régression non linéaire ?
Les deux sont des types de problèmes de régression. La différence entre les deux réside dans les données sur lesquelles ils sont formés.
Le modèle de régression linéaire suppose une relation linéaire entre les caractéristiques et les étiquettes, ce qui signifie que si nous prenons tous les points de données et les traçons sur une ligne linéaire (droite), cela devrait correspondre aux données.
Les modèles de régression non linéaire supposent qu'il n'y a pas de relation linéaire entre les variables. Les lignes non linéaires (curvilignes) doivent séparer et ajuster correctement les données.
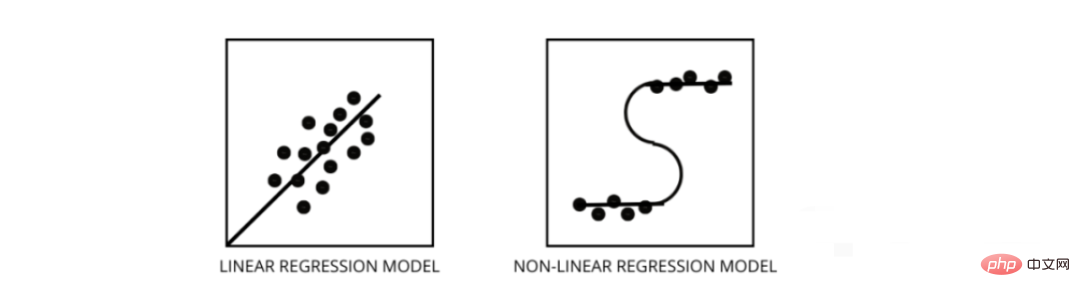
Trois meilleures façons de savoir si vos données sont linéaires ou non linéaires -
- Tracés résiduels
- Nuages de points
- En supposant que les données sont linéaires, entraînez un modèle linéaire et évaluez-le par précision.
4. Qu'est-ce que la multicolinéarité et comment affecte-t-elle les performances du modèle ?
La multicolinéarité se produit lorsque certaines caractéristiques sont fortement corrélées les unes aux autres. La corrélation fait référence à une mesure qui indique comment une variable est affectée par les changements d'une autre variable.
Si une augmentation de la caractéristique a entraîne une augmentation de la caractéristique b, alors les deux caractéristiques sont positivement corrélées. Si une augmentation de a entraîne une diminution de la caractéristique b, alors les deux caractéristiques sont corrélées négativement. Avoir deux variables hautement corrélées sur les données d'entraînement entraînera une multicolinéarité car son modèle ne sera pas en mesure de trouver des modèles dans les données, ce qui entraînera de mauvaises performances du modèle. Par conséquent, avant d’entraîner le modèle, nous devons d’abord essayer d’éliminer la multicolinéarité.
5. Comment les valeurs aberrantes affectent-elles les performances des modèles de régression linéaire ?
Les valeurs aberrantes sont des points de données dont les valeurs diffèrent de la plage moyenne des points de données. Autrement dit, ces points sont différents des données ou hors du 3ème critère.
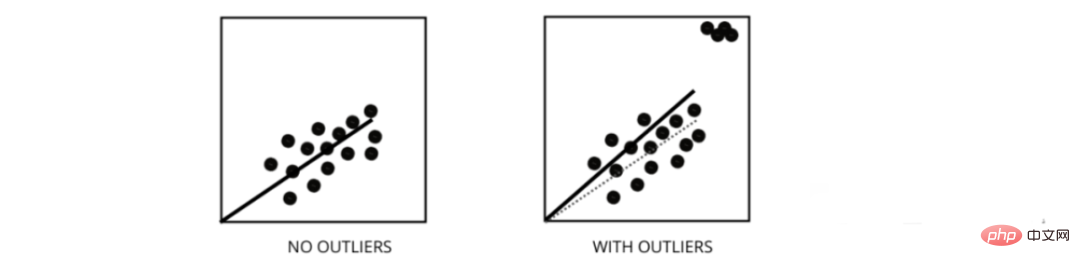
Le modèle de régression linéaire tente de trouver la ligne la mieux ajustée qui réduit les résidus. Si les données contiennent des valeurs aberrantes, la ligne de meilleur ajustement se déplacera un peu vers les valeurs aberrantes, ce qui augmentera le taux d'erreur et aboutira à un modèle avec une MSE très élevée.
6. Quelle est la différence entre MSE et MAE ?
MSE signifie erreur quadratique moyenne, qui est la différence au carré entre la valeur réelle et la valeur prédite. Et MAE est la différence absolue entre la valeur cible et la valeur prédite.
MSE pénalise les grosses erreurs, pas le MAE. À mesure que les valeurs de MSE et de MAE diminuent, le modèle tend vers une ligne mieux ajustée.
7. Que sont les régularisations L1 et L2 et quand faut-il les utiliser ?
Dans l'apprentissage automatique, notre objectif principal est de créer un modèle général capable de mieux fonctionner sur les données d'entraînement et de test, mais lorsqu'il y a très peu de données, les modèles de régression linéaire de base ont tendance à surajuster, nous utiliserons donc la régularisation l1 et l2. .
La régularisation L1 ou régression lasso fonctionne en ajoutant la valeur absolue de la pente comme terme de pénalité dans la fonction de coût. Aide à supprimer les valeurs aberrantes en supprimant tous les points de données dont les valeurs de pente sont inférieures à un seuil.
La régularisation L2 ou régression de crête ajoute un terme de pénalité égal au carré de la taille du coefficient. Cela pénalise les entités ayant des valeurs de pente plus élevées.
l1 et l2 sont utiles lorsque les données d'entraînement sont petites, que la variance est élevée, que les caractéristiques prédites sont plus grandes que les valeurs observées et que les données souffrent de multicolinéarité.
8. Que signifie l’hétéroscédasticité ?
Il fait référence à la situation dans laquelle les variances des points de données autour de la ligne la mieux ajustée sont différentes dans une plage. Il en résulte une dispersion inégale des résidus. S'il est présent dans les données, le modèle a tendance à prédire une sortie invalide. L’une des meilleures façons de tester l’hétéroscédasticité est de tracer les résidus.
L'une des principales causes de l'hétéroscédasticité au sein des données réside dans les grandes différences entre les caractéristiques des plages. Par exemple, si nous avons une colonne de 1 à 100 000, augmenter les valeurs de 10 % ne modifiera pas les valeurs inférieures, mais entraînera une très grande différence aux valeurs les plus élevées, produisant ainsi une grande différence de points de données. .
9. Quel est le rôle du facteur d’inflation de la variance ?
Le facteur d'inflation de la variance (vif) est utilisé pour déterminer dans quelle mesure une variable indépendante peut être prédite à l'aide d'autres variables indépendantes.
Prenons des exemples de données avec les fonctionnalités v1, v2, v3, v4, v5 et v6. Maintenant, pour calculer le vif de v1, considérez-le comme une variable prédictive et essayez de le prédire en utilisant toutes les autres variables prédictives.
Si la valeur de VIF est petite, alors il est préférable de supprimer la variable des données. Parce que des valeurs plus petites indiquent une corrélation élevée entre les variables.
10. Comment fonctionne la régression pas à pas ?
La régression pas à pas est une méthode de création d'un modèle de régression en supprimant ou en ajoutant des variables prédictives à l'aide de tests d'hypothèse. Il prédit la variable dépendante en testant de manière itérative la signification de chaque variable indépendante et en supprimant ou en ajoutant certaines fonctionnalités après chaque itération. Il s'exécute n fois et tente de trouver la meilleure combinaison de paramètres qui prédit la variable dépendante avec la plus petite erreur entre les valeurs observées et prédites.
Il peut gérer de grandes quantités de données de manière très efficace et résoudre des problèmes de grande dimension.
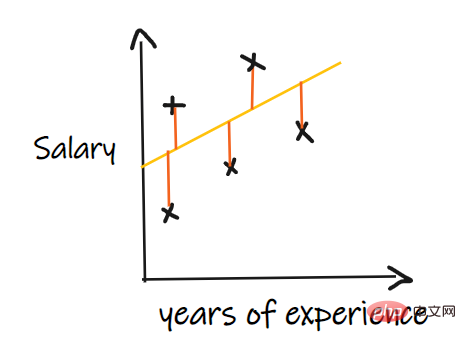
11. En plus du MSE et du MAE, existe-t-il d'autres indicateurs de régression importants ?

Nous utilisons un problème de régression pour introduire ces indicateurs, où notre entrée est l'expérience professionnelle et le résultat est le salaire. Le graphique ci-dessous montre une ligne de régression linéaire tracée pour prédire le salaire.
1. Erreur absolue moyenne (MAE) :
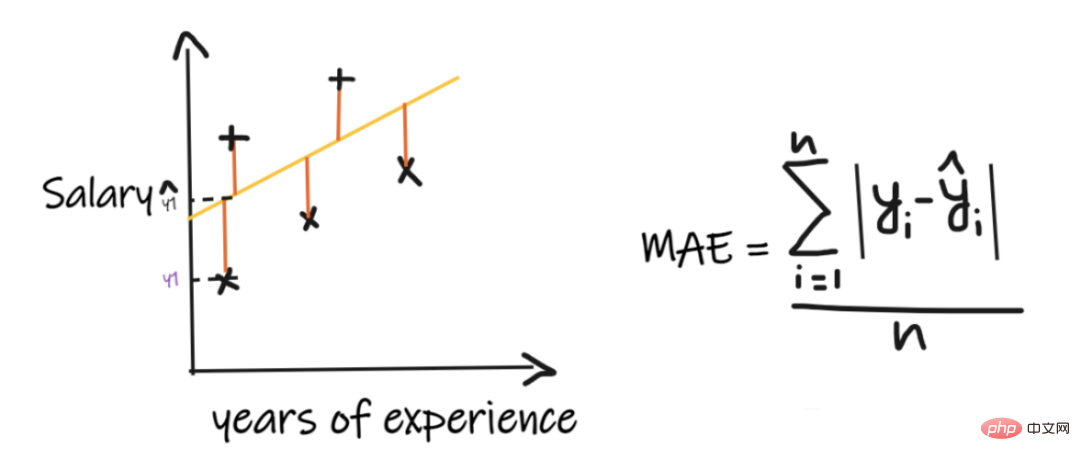
L'erreur absolue moyenne (MAE) est la métrique de régression la plus simple. Il ajoute la différence entre chaque valeur réelle et prédite et la divise par le nombre d'observations. Pour qu’un modèle de régression soit considéré comme un bon modèle, le MAE doit être aussi petit que possible.
Les avantages du MAE sont :
Simple et facile à comprendre. Le résultat aura les mêmes unités que la sortie. Par exemple : si l'unité de la colonne de sortie est LPA, alors si le MAE est de 1,2, alors nous pouvons interpréter le résultat comme +1,2 LPA ou -1,2 LPA, le MAE est relativement stable par rapport aux valeurs aberrantes (par rapport à certains autres indicateurs de régression, MAE est affecté par les valeurs aberrantes (moins d’impact). Les inconvénients de
MAE sont :
MAE utilise une fonction modulaire, mais la fonction modulaire n'est pas différentiable en tout point, elle ne peut donc pas être utilisée comme fonction de perte dans de nombreux cas.
2. Erreur quadratique moyenne (MSE) :
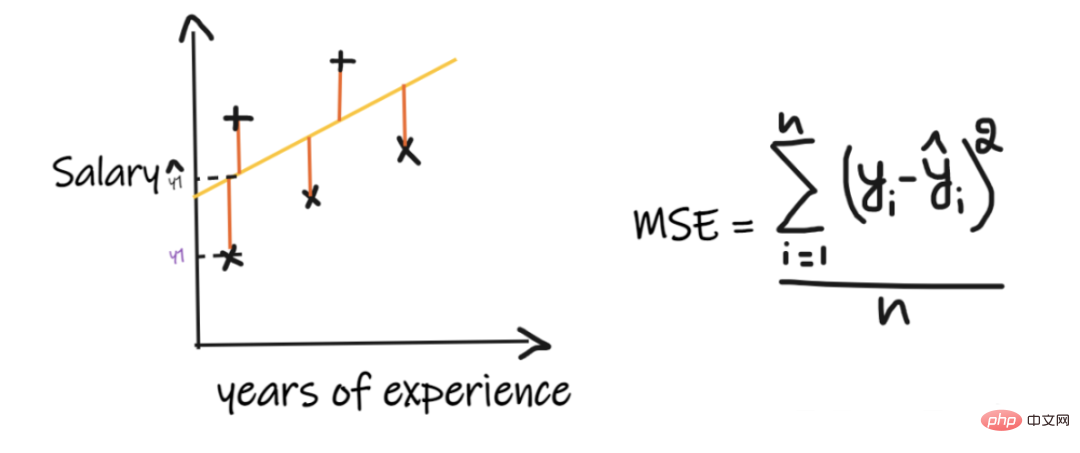
MSE prend la différence entre chaque valeur réelle et la valeur prédite, puis met la différence au carré et les additionne, enfin en la divisant par le nombre d'observations. Pour qu’un modèle de régression soit considéré comme un bon modèle, la MSE doit être aussi petite que possible.
Avantages du MSE : La fonction carré est dérivable en tous points, elle peut donc être utilisée comme fonction de perte.
Inconvénients de MSE : Étant donné que MSE utilise la fonction carré, l'unité du résultat est le carré de la sortie. Il est donc difficile d'interpréter les résultats. Puisqu'il utilise une fonction carrée, s'il y a des valeurs aberrantes dans les données, les différences seront également au carré et, par conséquent, le MSE n'est pas stable pour les valeurs aberrantes.
3. Erreur quadratique moyenne (RMSE) :
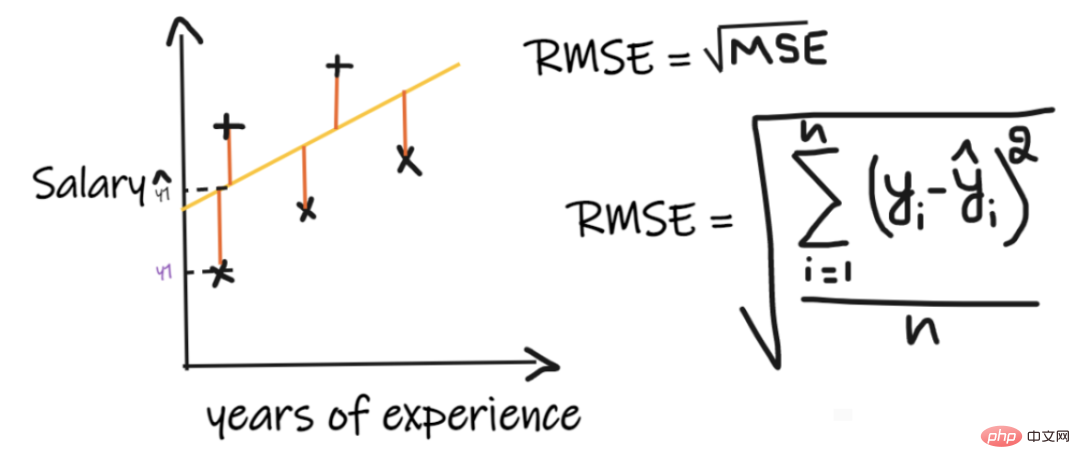
L'erreur quadratique moyenne (RMSE) prend la différence entre chaque valeur réelle et la valeur prédite, puis met la différence au carré et les additionne, et enfin divise par le nombre d'observations. Prenez ensuite la racine carrée du résultat. Par conséquent, RMSE est la racine carrée de MSE. Pour qu’un modèle de régression soit considéré comme un bon modèle, le RMSE doit être aussi petit que possible.
RMSE résout le problème du MSE, les unités seront les mêmes que celles de la sortie puisqu'il prend la racine carrée, mais est quand même moins stable aux valeurs aberrantes.
Les indicateurs ci-dessus dépendent du contexte du problème que nous résolvons. Nous ne pouvons pas juger de la qualité du modèle en regardant simplement les valeurs de MAE, MSE et RMSE sans comprendre le problème réel.
4, score R2 :
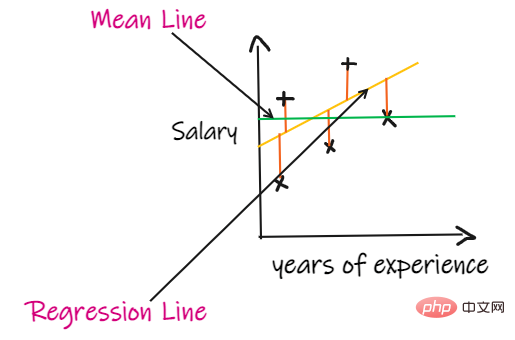
Si nous n'avons aucune donnée d'entrée, mais que nous voulons savoir combien de salaire il gagne dans cette entreprise, alors la meilleure chose que nous puissions faire est de leur donner la moyenne de tous les employés 'valeur des salaires.
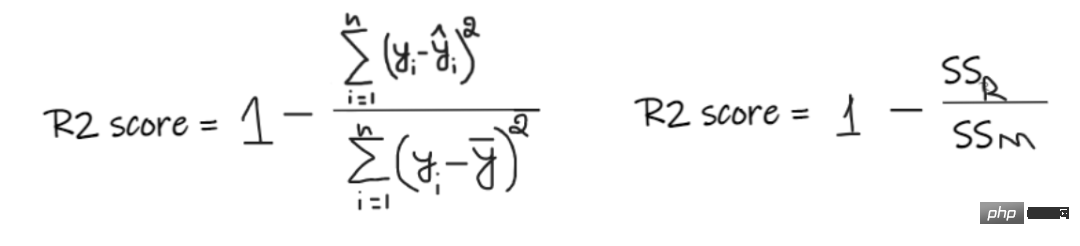
Le score R2 donne une valeur comprise entre 0 et 1 et peut être interprété pour n'importe quel contexte. Cela peut être compris comme la qualité de l’ajustement.
SSR est la somme des carrés des erreurs de la droite de régression, et SSM est la somme des carrés des erreurs de la moyenne mobile. Nous comparons la droite de régression à la droite moyenne.
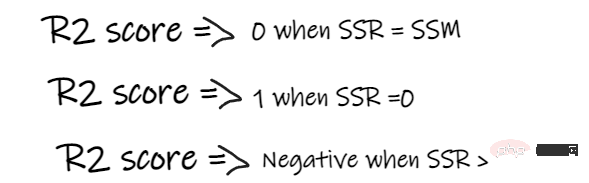
- Si le score R2 est de 0, cela signifie que notre modèle a les mêmes résultats que la moyenne, notre modèle doit donc être amélioré.
- Si le score R2 est de 1, le côté droit de l'équation devient 0, ce qui ne peut se produire que si notre modèle s'adapte à chaque point de données et ne commet aucune erreur.
- Si le score R2 est négatif, cela signifie que le côté droit de l'équation est supérieur à 1, ce qui peut arriver lorsque SSR > SSM. Cela signifie que notre modèle est pire que la moyenne, ce qui signifie que notre modèle est pire que de prendre la moyenne pour prédire
Si notre modèle a un score R2 de 0,8, cela signifie que nous pouvons dire que le modèle est capable d'expliquer 80 % de la variance de sortie. Autrement dit, 80 % de la variation des salaires peut s’expliquer par l’intrant (années de travail), mais les 20 % restants sont inconnus.
Si notre modèle comporte 2 fonctionnalités, les années de travail et les scores d'entretien, alors notre modèle peut expliquer 80 % des changements de salaire en utilisant ces deux fonctionnalités d'entrée.
Inconvénients de R2 :
À mesure que le nombre de fonctionnalités en entrée augmente, R2 aura tendance à augmenter en conséquence ou à rester le même, mais ne diminuera jamais, même si les fonctionnalités en entrée ne sont pas importantes pour notre modèle (par exemple, en ajoutant le nombre des caractéristiques d'entrée le jour de l'entretien) En ajoutant la température de l'air à notre exemple, R2 ne baissera pas même si la température n'est pas importante pour la sortie).
5. Score R2 ajusté :
Dans la formule ci-dessus, R2 est R2, n est le nombre d'observations (lignes) et p est le nombre de caractéristiques indépendantes. R2 ajusté résout les problèmes de R2.
Lorsque nous ajoutons des fonctionnalités moins importantes pour notre modèle, comme l'ajout de température pour prédire le salaire.....

Lors de l'ajout de fonctionnalités importantes pour le modèle, telles que l'ajout de scores d'entretien pour prédire le salaire...

Ce qui précède présente les points de connaissance importants des problèmes de régression et l'introduction de divers indicateurs importants utilisés pour résoudre problèmes de régression. Avantages et inconvénients, j'espère que cela vous aidera.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1393
1393
 52
52
 1207
1207
 24
24
 Cet article vous amènera à comprendre SHAP : explication du modèle pour l'apprentissage automatique
Jun 01, 2024 am 10:58 AM
Cet article vous amènera à comprendre SHAP : explication du modèle pour l'apprentissage automatique
Jun 01, 2024 am 10:58 AM
Dans les domaines de l’apprentissage automatique et de la science des données, l’interprétabilité des modèles a toujours été au centre des préoccupations des chercheurs et des praticiens. Avec l'application généralisée de modèles complexes tels que l'apprentissage profond et les méthodes d'ensemble, la compréhension du processus décisionnel du modèle est devenue particulièrement importante. Explainable AI|XAI contribue à renforcer la confiance dans les modèles d'apprentissage automatique en augmentant la transparence du modèle. L'amélioration de la transparence des modèles peut être obtenue grâce à des méthodes telles que l'utilisation généralisée de plusieurs modèles complexes, ainsi que les processus décisionnels utilisés pour expliquer les modèles. Ces méthodes incluent l'analyse de l'importance des caractéristiques, l'estimation de l'intervalle de prédiction du modèle, les algorithmes d'interprétabilité locale, etc. L'analyse de l'importance des fonctionnalités peut expliquer le processus de prise de décision du modèle en évaluant le degré d'influence du modèle sur les fonctionnalités d'entrée. Estimation de l’intervalle de prédiction du modèle
 KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
KAN, qui remplace MLP, a été étendu à la convolution par des projets open source
Jun 01, 2024 pm 10:03 PM
Plus tôt ce mois-ci, des chercheurs du MIT et d'autres institutions ont proposé une alternative très prometteuse au MLP – KAN. KAN surpasse MLP en termes de précision et d’interprétabilité. Et il peut surpasser le MLP fonctionnant avec un plus grand nombre de paramètres avec un très petit nombre de paramètres. Par exemple, les auteurs ont déclaré avoir utilisé KAN pour reproduire les résultats de DeepMind avec un réseau plus petit et un degré d'automatisation plus élevé. Plus précisément, le MLP de DeepMind compte environ 300 000 paramètres, tandis que le KAN n'en compte qu'environ 200. KAN a une base mathématique solide comme MLP est basé sur le théorème d'approximation universelle, tandis que KAN est basé sur le théorème de représentation de Kolmogorov-Arnold. Comme le montre la figure ci-dessous, KAN a
 Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Implémentation d'algorithmes d'apprentissage automatique en C++ : défis et solutions courants
Jun 03, 2024 pm 01:25 PM
Les défis courants rencontrés par les algorithmes d'apprentissage automatique en C++ incluent la gestion de la mémoire, le multithread, l'optimisation des performances et la maintenabilité. Les solutions incluent l'utilisation de pointeurs intelligents, de bibliothèques de threads modernes, d'instructions SIMD et de bibliothèques tierces, ainsi que le respect des directives de style de codage et l'utilisation d'outils d'automatisation. Des cas pratiques montrent comment utiliser la bibliothèque Eigen pour implémenter des algorithmes de régression linéaire, gérer efficacement la mémoire et utiliser des opérations matricielles hautes performances.
 Surpassant largement le DPO : l'équipe de Chen Danqi a proposé une optimisation simple des préférences SimPO et a également affiné le modèle open source 8B le plus puissant.
Jun 01, 2024 pm 04:41 PM
Surpassant largement le DPO : l'équipe de Chen Danqi a proposé une optimisation simple des préférences SimPO et a également affiné le modèle open source 8B le plus puissant.
Jun 01, 2024 pm 04:41 PM
Afin d'aligner les grands modèles de langage (LLM) sur les valeurs et les intentions humaines, il est essentiel d'apprendre les commentaires humains pour garantir qu'ils sont utiles, honnêtes et inoffensifs. En termes d'alignement du LLM, une méthode efficace est l'apprentissage par renforcement basé sur le retour humain (RLHF). Bien que les résultats de la méthode RLHF soient excellents, certains défis d’optimisation sont impliqués. Cela implique de former un modèle de récompense, puis d'optimiser un modèle politique pour maximiser cette récompense. Récemment, certains chercheurs ont exploré des algorithmes hors ligne plus simples, dont l’optimisation directe des préférences (DPO). DPO apprend le modèle politique directement sur la base des données de préférence en paramétrant la fonction de récompense dans RLHF, éliminant ainsi le besoin d'un modèle de récompense explicite. Cette méthode est simple et stable
 Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
Aucune donnée OpenAI requise, rejoignez la liste des grands modèles de code ! UIUC publie StarCoder-15B-Instruct
Jun 13, 2024 pm 01:59 PM
À la pointe de la technologie logicielle, le groupe de l'UIUC Zhang Lingming, en collaboration avec des chercheurs de l'organisation BigCode, a récemment annoncé le modèle de grand code StarCoder2-15B-Instruct. Cette réalisation innovante a permis une percée significative dans les tâches de génération de code, dépassant avec succès CodeLlama-70B-Instruct et atteignant le sommet de la liste des performances de génération de code. Le caractère unique de StarCoder2-15B-Instruct réside dans sa stratégie d'auto-alignement pur. L'ensemble du processus de formation est ouvert, transparent et complètement autonome et contrôlable. Le modèle génère des milliers d'instructions via StarCoder2-15B en réponse au réglage fin du modèle de base StarCoder-15B sans recourir à des annotations manuelles coûteuses.
 Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
Cinq écoles d'apprentissage automatique que vous ne connaissez pas
Jun 05, 2024 pm 08:51 PM
L'apprentissage automatique est une branche importante de l'intelligence artificielle qui donne aux ordinateurs la possibilité d'apprendre à partir de données et d'améliorer leurs capacités sans être explicitement programmés. L'apprentissage automatique a un large éventail d'applications dans divers domaines, de la reconnaissance d'images et du traitement du langage naturel aux systèmes de recommandation et à la détection des fraudes, et il change notre façon de vivre. Il existe de nombreuses méthodes et théories différentes dans le domaine de l'apprentissage automatique, parmi lesquelles les cinq méthodes les plus influentes sont appelées les « Cinq écoles d'apprentissage automatique ». Les cinq grandes écoles sont l’école symbolique, l’école connexionniste, l’école évolutionniste, l’école bayésienne et l’école analogique. 1. Le symbolisme, également connu sous le nom de symbolisme, met l'accent sur l'utilisation de symboles pour le raisonnement logique et l'expression des connaissances. Cette école de pensée estime que l'apprentissage est un processus de déduction inversée, à travers les connaissances existantes.
 IA explicable : Expliquer les modèles IA/ML complexes
Jun 03, 2024 pm 10:08 PM
IA explicable : Expliquer les modèles IA/ML complexes
Jun 03, 2024 pm 10:08 PM
Traducteur | Revu par Li Rui | Chonglou Les modèles d'intelligence artificielle (IA) et d'apprentissage automatique (ML) deviennent aujourd'hui de plus en plus complexes, et le résultat produit par ces modèles est une boîte noire – impossible à expliquer aux parties prenantes. L'IA explicable (XAI) vise à résoudre ce problème en permettant aux parties prenantes de comprendre comment fonctionnent ces modèles, en s'assurant qu'elles comprennent comment ces modèles prennent réellement des décisions et en garantissant la transparence des systèmes d'IA, la confiance et la responsabilité pour résoudre ce problème. Cet article explore diverses techniques d'intelligence artificielle explicable (XAI) pour illustrer leurs principes sous-jacents. Plusieurs raisons pour lesquelles l’IA explicable est cruciale Confiance et transparence : pour que les systèmes d’IA soient largement acceptés et fiables, les utilisateurs doivent comprendre comment les décisions sont prises
 Flash Attention est-il stable ? Meta et Harvard ont constaté que les écarts de poids de leur modèle fluctuaient de plusieurs ordres de grandeur.
May 30, 2024 pm 01:24 PM
Flash Attention est-il stable ? Meta et Harvard ont constaté que les écarts de poids de leur modèle fluctuaient de plusieurs ordres de grandeur.
May 30, 2024 pm 01:24 PM
MetaFAIR s'est associé à Harvard pour fournir un nouveau cadre de recherche permettant d'optimiser le biais de données généré lors de l'apprentissage automatique à grande échelle. On sait que la formation de grands modèles de langage prend souvent des mois et utilise des centaines, voire des milliers de GPU. En prenant comme exemple le modèle LLaMA270B, sa formation nécessite un total de 1 720 320 heures GPU. La formation de grands modèles présente des défis systémiques uniques en raison de l’ampleur et de la complexité de ces charges de travail. Récemment, de nombreuses institutions ont signalé une instabilité dans le processus de formation lors de la formation des modèles d'IA générative SOTA. Elles apparaissent généralement sous la forme de pics de pertes. Par exemple, le modèle PaLM de Google a connu jusqu'à 20 pics de pertes au cours du processus de formation. Le biais numérique est à l'origine de cette imprécision de la formation,



