Vers une IA vérifiable : cinq défis des méthodes formelles
L'intelligence artificielle est un système informatique qui tente d'imiter l'intelligence humaine, y compris certaines fonctions humaines intuitivement liées à l'intelligence, telles que l'apprentissage, la résolution de problèmes, la pensée et l'action rationnelles. Interprété au sens large, le terme IA recouvre de nombreux domaines étroitement liés tels que l’apprentissage automatique. Les systèmes qui font largement appel à l’IA ont des impacts sociaux importants dans des domaines tels que la santé, les transports, la finance, les réseaux sociaux, le commerce électronique et l’éducation.
Cet impact social croissant a également entraîné une série de risques et de préoccupations, notamment des erreurs dans les logiciels d'intelligence artificielle, des cyberattaques et la sécurité des systèmes d'intelligence artificielle. Par conséquent, la question de la vérification des systèmes d’IA, et le sujet plus large de l’IA digne de confiance, ont commencé à attirer l’attention de la communauté des chercheurs. « L'IA vérifiable » a été établie comme objectif pour la conception de systèmes d'IA, un système d'IA vérifiable avec des garanties d'exactitude solides et idéalement prouvables sur des exigences mathématiques spécifiques. Comment pouvons-nous atteindre cet objectif ?
Récemment, un article de synthèse dans "The Communications of ACM" a tenté de réfléchir aux défis auxquels est confrontée l'IA vérifiable du point de vue de la vérification formelle et a proposé des solutions de principe. Les auteurs sont le professeur S. Shankar Sastry et Sanjit A. Seshia, directeur du département de génie électrique et d'informatique de l'UC Berkeley, et Dorsa Sadigh, professeur adjoint d'informatique à l'université de Stanford.
En informatique et en ingénierie, les méthodes formelles impliquent la spécification mathématique rigoureuse, la conception et la vérification des systèmes. À la base, les méthodes formelles concernent la preuve : formuler des spécifications qui constituent les obligations de preuve, concevoir des systèmes pour remplir ces obligations et vérifier par des recherches de preuves algorithmiques que le système est effectivement conforme à ses spécifications. Des tests et simulations basés sur les spécifications à la vérification de modèles et à la démonstration de théorèmes, une gamme de méthodes formelles sont couramment utilisées dans la conception assistée par ordinateur de circuits intégrés et ont été largement utilisées pour trouver des bogues dans les logiciels, analyser des systèmes cyber-physiques et découvrir la sécurité. vulnérabilités.
Cet article passe en revue les méthodes d'application traditionnelles des méthodes formelles et souligne cinq défis uniques des méthodes formelles dans les systèmes d'IA, notamment :
- Développement de langages et d'algorithmes sur l'environnement
- Abstrait et représente des composants et des systèmes ML complexes
- proposez les nouvelles méthodes et propriétés formelles canoniques pour les systèmes et données d'IA - Développez un moteur informatique évolutif pour les algorithmes de développement inférieurs automatisés
- Develop et techniques pour une conception fiable par construction
- Sur la base de l'analyse des derniers progrès, l'auteur propose des principes pour résoudre les défis ci-dessus. Cet article ne se concentre pas uniquement sur un type spécifique de composant d’IA tel que les réseaux de neurones profonds, ou sur une méthode spécifique telle que l’apprentissage par renforcement, mais tente de couvrir un éventail plus large de systèmes d’IA et de leurs processus de conception. De plus, les méthodes formelles ne constituent qu’un chemin vers une IA fiable. Les idées présentées dans cet article sont donc destinées à compléter les méthodes d’autres domaines. Ces perspectives s’appuient largement sur la réflexion sur les enjeux liés à l’utilisation de l’IA dans les systèmes autonomes et semi-autonomes, où les enjeux de sécurité et de vérification sont plus importants.
Vue d'ensemble La figure 1 montre un processus typique de vérification formelle, de synthèse formelle et de résilience d'exécution formellement guidée. Le processus de vérification formelle commence par trois entrées :
Figure 1 : Approche formelle pour la vérification, la synthèse et la résilience d'exécution
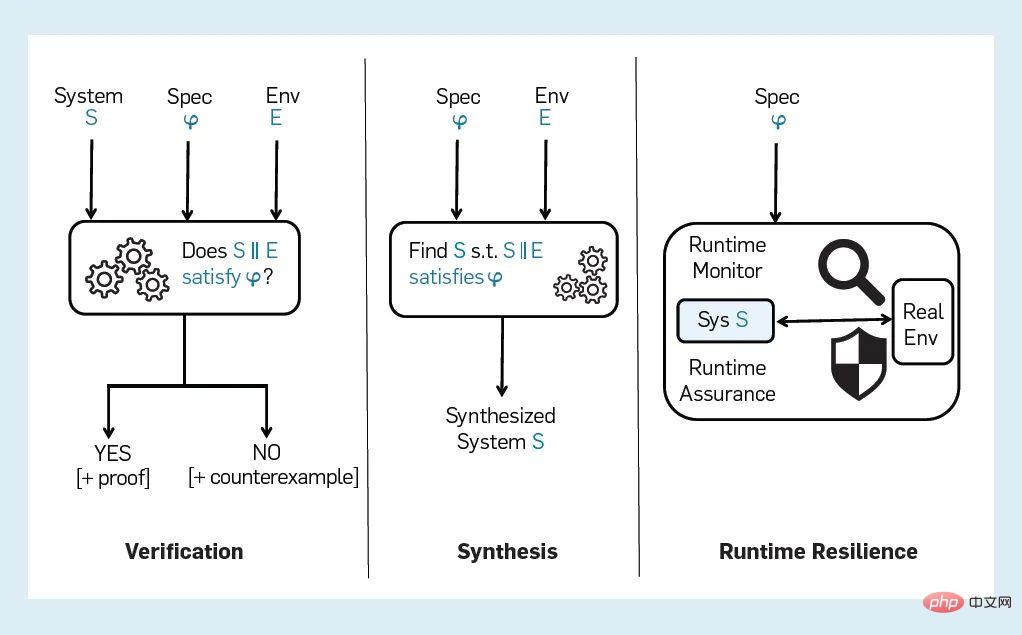
- Modèle de système S à vérifier
- Modèle d'environnement E
- Attributs à vérifier Φ
Le vérificateur génère une réponse par oui ou par non comme sortie pour indiquer si S satisfait la propriété Φ dans l'environnement E. Généralement, la sortie « non » est accompagnée d'un contre-exemple, également appelé trace d'erreur, qui est une exécution du système montrant comment Φ a été falsifié. Certains outils de validation incluent également une preuve d'exactitude ou un certificat avec une réponse « oui ». Nous adoptons une perspective large sur les méthodes formelles, y compris toute technique utilisant un aspect de spécification formelle, de vérification ou de synthèse. Par exemple, nous incluons des méthodes de vérification matérielle basées sur la simulation ou des méthodes de test logiciel basées sur des modèles, car elles utilisent également des spécifications ou des modèles formels pour guider le processus de simulation ou de test.
Pour appliquer la vérification formelle à un système d'IA, il faut être capable de représenter formellement au moins les trois entrées S, E et Φ. Idéalement, il y aura une procédure de prise de décision efficace pour répondre au « oui ». Question « décrite plus tôt / Non ». Cependant, il n’est pas trivial de construire une bonne représentation même pour trois entrées, et encore moins de gérer la complexité des problèmes sous-jacents de conception et de vérification.
Nous illustrons ici le propos de cet article à travers un exemple issu du domaine de la conduite semi-autonome. La figure 2 montre un exemple illustratif d'un système d'IA : un CPS en boucle fermée qui comprend un véhicule semi-autonome avec un composant d'apprentissage automatique et son environnement. Plus précisément, supposons qu'un véhicule « ego » semi-autonome dispose d'un système de freinage d'urgence automatisé (AEBS) qui tente de détecter et de classer les objets devant lui et d'appliquer les freins lorsque cela est nécessaire pour éviter une collision. Dans la figure 2, un AEBS se compose d'un contrôleur (freinage autonome), d'un objet contrôlé (sous-système contrôlé du véhicule, y compris d'autres parties de la pile d'autonomie) et d'un capteur (caméra), ainsi que d'un composant de perception utilisant le DNN. L'AEBS est combiné à l'environnement du véhicule pour former un CPS en boucle fermée. L'environnement d'un « soi » véhicule comprend des agents et des objets à l'extérieur du véhicule (autres véhicules, piétons, etc.) ainsi qu'à l'intérieur du véhicule (par exemple, le conducteur). Les exigences de sécurité d'un tel système en boucle fermée peuvent être caractérisées de manière informelle en termes de propriété de maintenir une distance de sécurité entre le véhicule « ego » en mouvement et tout autre agent ou objet sur la route. Il existe cependant de nombreuses nuances dans la spécification, la modélisation et la vérification de tels systèmes.
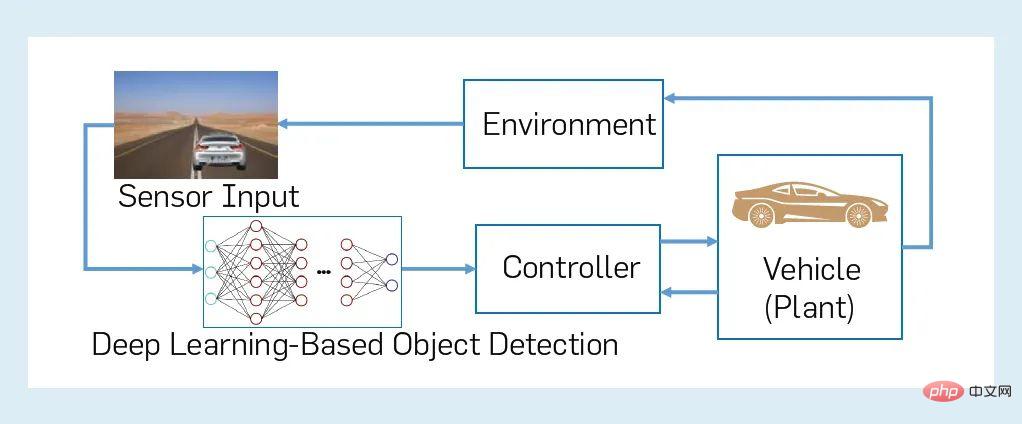
Figure 2 : Exemple de CPS en boucle fermée avec composant d'apprentissage automatique
Tout d'abord, pensez à modéliser l'environnement d'un véhicule semi-autonome. Même des questions telles que le nombre et les agents (humains et non humains) présents dans l'environnement, sans parler de leurs propriétés et de leurs comportements, peuvent être sujettes à une incertitude considérable. Deuxièmement, les tâches de perception utilisant l’IA ou le ML sont difficiles, voire impossibles, à formaliser. Troisièmement, les composants tels que les DNN peuvent être des objets complexes de grande dimension qui fonctionnent sur des espaces d'entrée complexes de grande dimension. Par conséquent, il est très difficile de générer les trois entrées S, E, Φ du processus de vérification formelle, même sous une forme qui rend la vérification réalisable.
Si quelqu'un résout ce problème, il sera difficile de vérifier un CPS basé sur l'IA aussi complexe que la figure 2. Dans un tel CPS, une approche compositionnelle (modulaire) est cruciale pour l’évolutivité, mais elle peut être difficile à mettre en œuvre en raison de facteurs tels que la difficulté de spécification de la composition. Enfin, l’approche correcte par construction (CBC) est prometteuse pour une IA vérifiable, mais elle en est encore à ses balbutiements et repose largement sur les progrès en matière de spécification et de vérification. La figure 3 résume les cinq domaines difficiles de l’IA vérifiable. Pour chaque domaine, nous distillons les approches prometteuses actuelles en trois principes pour surmonter les défis, représentés sous forme de nœuds. Les bords entre les nœuds montrent quels principes de l'IA vérifiable dépendent les uns des autres, avec des fils de dépendance communs représentés par une seule couleur. Ces défis et les principes correspondants sont développés ci-dessous.
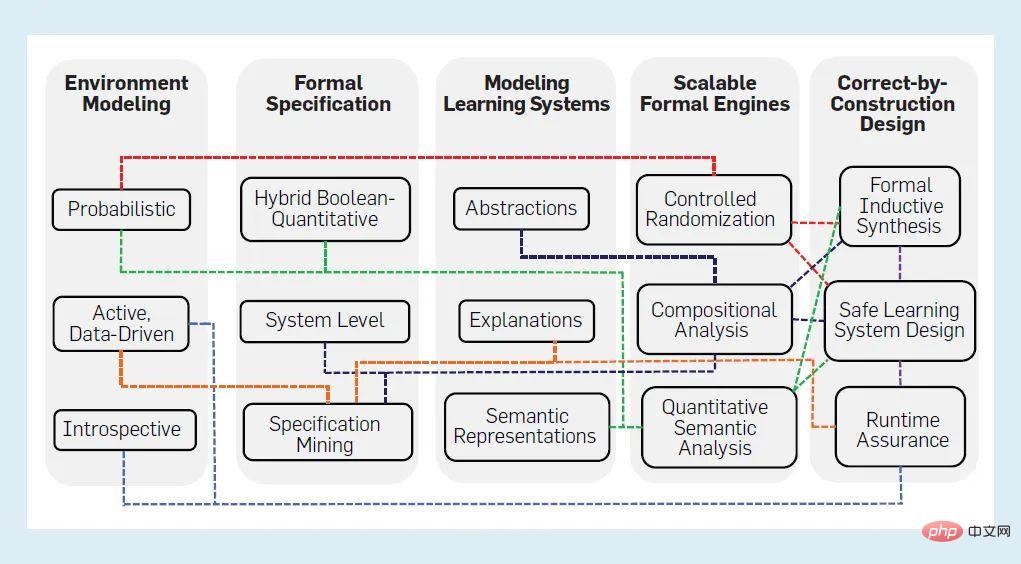
Figure 3 : Résumé de 5 domaines de défi de l'IA vérifiable
Modélisation de l'environnement
L'environnement dans lequel les systèmes basés sur l'IA/ML fonctionnent est généralement complexe, comme les différentes villes où fonctionnent des véhicules autonomes. environnements de circulation. En fait, l’IA/ML est souvent introduite dans ces systèmes pour faire face à la complexité et à l’incertitude de l’environnement. Les processus de conception ML actuels utilisent souvent des données pour spécifier implicitement l'environnement. L’objectif de nombreux systèmes d’IA est de découvrir et de comprendre leur environnement au fur et à mesure de leur fonctionnement, contrairement aux systèmes traditionnels conçus pour un environnement spécifié a priori. Cependant, toute vérification formelle et synthèse sont liées à un modèle de l’environnement. Par conséquent, les hypothèses et les propriétés concernant les données d'entrée doivent être interprétées dans le modèle d'environnement. Nous distillons cette dichotomie en trois défis pour la modélisation de l'environnement des systèmes d'IA et développons des principes correspondants pour relever ces défis.
2.1 Incertitude de modélisation
Dans l'utilisation traditionnelle de la vérification formelle, une approche courante consiste à modéliser l'environnement comme un processus non déterministe contraint, ou une « perturbation ». Cette « surapproximation » de la modélisation environnementale permet de saisir l’incertitude environnementale de manière plus conservatrice sans nécessiter de modèles trop détaillés qui seraient inefficaces pour l’inférence. Cependant, pour l’autonomie basée sur l’IA, une modélisation purement non déterministe peut produire trop de faux rapports d’erreurs, rendant le processus de vérification inutile en pratique. Par exemple, lors de la modélisation du comportement des véhicules environnants d’une voiture autonome, les comportements des véhicules environnants sont divers. Si une modélisation purement non déterministe est adoptée, les accidents qui se produisent toujours de manière inattendue ne peuvent pas être pris en compte. De plus, de nombreux systèmes d’IA/ML font implicitement ou explicitement des hypothèses distributionnelles sur les données ou le comportement de l’environnement, nécessitant une modélisation probabiliste. Puisqu’il est difficile de déterminer avec précision la distribution sous-jacente, le modèle probabiliste résultant ne peut pas être considéré comme parfait et les incertitudes du processus de modélisation doivent être caractérisées dans le modèle lui-même.
Modélisation formelle probabiliste. Pour relever ce défi, nous proposons une forme qui combine modélisation probabiliste et non déterministe. La modélisation probabiliste peut être utilisée lorsqu'une distribution de probabilité peut être spécifiée ou estimée de manière fiable. Dans d’autres cas, la modélisation non déterministe peut être utilisée pour surestimer le comportement environnemental. Alors que des formalismes tels que les processus décisionnels de Markov offrent déjà un moyen de mélanger des approches probabilistes et non déterministes, nous pensons que des formalismes plus riches tels que le paradigme de programmation probabiliste peuvent fournir une modélisation plus expressive et procédurale de l'environnement. Nous prévoyons que dans de nombreux cas, ces procédures probabilistes devront être apprises (en partie) à partir de données ou synthétisées. À ce stade, toute incertitude sur les paramètres appris doit être propagée au reste du système et représentée dans le modèle probabiliste. Par exemple, les processus de décision markoviens convexes fournissent un moyen de représenter l'incertitude dans les valeurs de probabilité de transition apprises et d'étendre les algorithmes de validation et de contrôle pour tenir compte de cette incertitude.
2.2 Variables inconnues
Dans les domaines de vérification formelle traditionnels tels que la vérification des pilotes de périphériques, l'interface entre le système S et son environnement E est bien définie, et E ne peut communiquer avec S que via cette interface pour interagir. Cette interface est incomplète pour l’autonomie basée sur l’IA, car elle est dictée par des composants de capteurs et de perception qui ne capturent que partiellement et bruyamment l’environnement et ne peuvent pas capturer toutes les interactions entre S et E. Toutes les variables (caractéristiques) de l'environnement sont connues, sans parler des variables perçues. Même dans des scénarios restreints où les variables environnementales sont connues, il existe un manque flagrant d’informations sur leur évolution, notamment au moment de la conception. De plus, la modélisation de capteurs tels que le lidar qui représentent les interfaces environnementales constitue un défi technique important.
Modélisation d'environnement introspective. Nous proposons de résoudre ce problème en développant des méthodes de conception et de vérification introspectives, c'est-à-dire en effectuant une introspection dans un système S pour identifier algorithmiquement une hypothèse A sur l'environnement E qui est suffisante pour garantir que la spécification Φ est satisfaite. Idéalement, A doit être la plus faible de ces hypothèses, et doit également être suffisamment efficace pour générer au moment de la conception, surveiller au moment de l'exécution les capteurs disponibles et d'autres sources d'informations sur l'environnement, et faciliter la détection lorsque les hypothèses sont violées. être pris. De plus, si un opérateur humain est impliqué, on pourrait espérer que A puisse être traduit en une explication intelligible, c'est-à-dire que S puisse « expliquer » à un humain pourquoi il pourrait ne pas satisfaire à la spécification Φ. La gestion de ces multiples exigences, ainsi que la nécessité de bons modèles de capteurs, font de la modélisation des environnements introspectifs un problème très important. Des travaux préliminaires montrent que cette extraction d'hypothèses contrôlables est réalisable dans des cas simples, même si des travaux supplémentaires sont nécessaires pour la rendre pratique.
2.3 Simulation du comportement humain
Pour de nombreux systèmes d'IA, tels que les voitures semi-autonomes, les agents humains sont un élément essentiel de l'environnement et du système. Les modèles artificiels d’êtres humains ne parviennent pas à capturer de manière adéquate la variabilité et l’incertitude du comportement humain. D'un autre côté, les approches basées sur les données pour modéliser le comportement humain peuvent être sensibles à l'expressivité et à la qualité des données des fonctionnalités utilisées par le modèle ML. Pour atteindre un degré élevé d’assurance pour les systèmes d’IA humaine, nous devons remédier aux limites des techniques de modélisation humaine actuelles et fournir une assurance sur leur précision prédictive et leur convergence.
Modélisation proactive basée sur les données. Nous pensons que la modélisation humaine nécessite une approche active basée sur les données et que la structure et les caractéristiques du modèle représentées mathématiquement conviennent aux méthodes formelles. Un élément clé de la modélisation humaine consiste à capturer l’intention humaine. Nous proposons une approche en trois volets : définir des modèles ou des fonctionnalités du modèle sur la base de connaissances d'experts, utiliser l'apprentissage hors ligne pour compléter le modèle en vue d'une utilisation au moment de la conception, et apprendre et mettre à jour le modèle d'environnement au moment de l'exécution en surveillant et en interagissant avec l'environnement. Par exemple, il a été démontré que les données collectées à partir de simulateurs de conduite grâce à des expériences avec des sujets humains peuvent être utilisées pour générer des modèles comportementaux de conducteurs humains pouvant être utilisés pour valider et contrôler des véhicules autonomes. En outre, les techniques d'entraînement et d'attaque contradictoires dans le domaine de la sécurité informatique peuvent être utilisées pour l'apprentissage actif de modèles humains et pour la conception ultérieure de modèles pour des actions humaines spécifiques conduisant à un comportement dangereux. Ces techniques peuvent aider à développer des algorithmes de vérification pour les systèmes humain-IA.
Spécifications formelles
La vérification formelle repose en grande partie sur des spécifications formelles - des déclarations mathématiques précises de ce qu'un système doit faire. Même dans les domaines où les méthodes formelles ont connu un succès considérable, l’élaboration de spécifications formelles de haute qualité constitue un défi, et les systèmes d’IA en particulier sont confrontés à des défis uniques.
3.1 Tâche difficile à formaliser
Le module de perception du contrôleur AEBS de la figure 2 doit détecter et classer les objets, distinguant ainsi les véhicules et les piétons des autres entités. La précision de ce module nécessite une définition formelle de chaque type d'usager de la route et d'objet, ce qui est extrêmement difficile au sens de la méthode formelle classique. Ce problème existe dans toutes les implémentations de ce module de perception, pas seulement dans les méthodes basées sur l'apprentissage profond. Des problèmes similaires surviennent avec d’autres tâches impliquant la perception et la communication, comme le traitement du langage naturel. Alors, comment spécifier l’attribut de précision pour un tel module ? Quel devrait être le langage de spécification ? Quels outils pouvons-nous utiliser pour construire des spécifications ?
Spécifications de bout en bout/au niveau du système. Afin de relever les défis ci-dessus, nous pouvons légèrement modifier ce problème. Plutôt que de spécifier directement des tâches difficiles à formaliser, nous devrions d’abord nous concentrer sur la spécification précise du comportement de bout en bout d’un système d’IA. A partir de cette spécification au niveau système, des contraintes sur les interfaces entrée-sortie des composants difficiles à formaliser peuvent être obtenues. Ces contraintes servent de spécification au niveau des composants qui est contextuellement pertinente pour l'ensemble du système d'IA. Pour l'exemple AEBS de la figure 2, cela implique la spécification de la propriété Φ, qui consiste à maintenir une distance minimale de tout objet pendant le mouvement, à partir de laquelle nous pouvons déduire des contraintes sur l'espace d'entrée DNN à capturer sémantiquement dans l'analyse contradictoire. Espace d'entrée significatif .
3.2 Spécifications quantitatives et spécifications booléennes
Traditionnellement, les spécifications formelles ont tendance à être booléennes, qui mappent un comportement de système donné à « vrai » ou « faux ». Cependant, en IA et en ML, les spécifications sont souvent présentées comme des fonctions objectives qui régulent les coûts ou les récompenses. En outre, il peut y avoir plusieurs objectifs, dont certains doivent être atteints ensemble, tandis que d’autres peuvent nécessiter des compromis les uns contre les autres dans certaines circonstances. Quelle est la meilleure manière d’unifier les deux approches normatives, booléenne et quantitative ? Existe-t-il un formalisme qui capture uniformément les propriétés communes des composants de l’IA, telles que la robustesse et l’équité ?
Mélanger les spécifications quantitatives et booléennes. Les spécifications booléennes et quantitatives ont leurs avantages : les spécifications booléennes sont plus faciles à composer, mais les fonctions objectives facilitent la validation et la synthèse avec des techniques basées sur l'optimisation et définissent une granularité plus fine de la satisfaction des propriétés. Une façon de combler cet écart consiste à passer à des langages de spécification quantitative, par exemple en utilisant la logique avec une sémantique booléenne et quantitative (telle que la logique temporelle métrique), ou en combinant des automates avec des fonctions de récompense pour RL. Une autre approche consiste à combiner les spécifications booléennes et quantitatives dans une structure de spécification commune, telle qu'un livre de règles, dans laquelle les spécifications peuvent être organisées, comparées et résumées dans une structure hiérarchique. La recherche a identifié plusieurs catégories de propriétés des systèmes d’IA, notamment la robustesse, l’équité, la confidentialité, la responsabilité et la transparence. Les chercheurs proposent de nouveaux formalismes reliant les idées des méthodes formelles et du ML pour modéliser les variations de ces propriétés telles que la robustesse sémantique.
3.3 Données et exigences formelles
La vue « les données sont des spécifications » est très courante dans l'apprentissage automatique. Les données étiquetées « réelles » sur un ensemble limité d’entrées sont souvent la seule spécification d’un comportement correct. Ceci est très différent des méthodes formelles, qui sont généralement données sous forme de logique ou d'automates, qui définissent l'ensemble des comportements corrects qui traversent toutes les entrées possibles. L’écart entre les données et les normes est remarquable, surtout lorsque les données sont limitées, biaisées ou proviennent de non-experts. Nous avons besoin de techniques pour formaliser les propriétés des données, qu’il s’agisse de données disponibles au moment de la conception ou de données non encore rencontrées.
Exploitation minière de spécifications. Pour combler le fossé entre les données et les spécifications formelles, nous proposons d'utiliser des algorithmes pour déduire des spécifications à partir de données et d'autres observations – ce que l'on appelle des techniques d'exploration de spécifications. Ce type d'approche peut souvent être utilisé pour les composants ML, y compris les composants de perception, car dans de nombreux cas, il n'est pas nécessaire d'avoir une spécification précise ou lisible par l'homme. Nous pouvons également utiliser des méthodes d’exploration de normes pour déduire les intentions humaines et d’autres propriétés à partir de démonstrations ou de formes plus complexes d’interactions entre plusieurs agents (humains et IA).
Modélisation des systèmes d'apprentissage
Dans la plupart des applications traditionnelles de vérification formelle, le système S est fixe et connu au moment de la conception, tel qu'il peut s'agir d'un programme, ou d'un programme utilisant un langage de programmation ou du matériel. Langage de description pour décrire les circuits. Le problème de modélisation du système consiste principalement à réduire S à une taille plus maniable en supprimant les détails non pertinents. Les systèmes d'IA apportent des défis très différents à la modélisation des systèmes, provenant principalement de l'utilisation de l'apprentissage automatique :
Espace d'entrée de haute dimension
Les composants ML pour la perception fonctionnent généralement à très haut niveau et fonctionnent sur une dimension espace de saisie. Par exemple, une image RVB d'entrée peut mesurer 1 000 x 600 pixels et contenir 256 ((1 000 x 600 x 3)) éléments. L'entrée est généralement un flux vectoriel de grande dimension comme celui-ci. Bien que les chercheurs aient utilisé des méthodes formelles pour les espaces d'entrée de grande dimension (comme dans les circuits numériques), la nature de l'espace d'entrée pour la perception basée sur le ML n'est pas entièrement booléenne, mais est mixte et comprend des variables discrètes et des variables continues. .
Paramètre/espace d'état de haute dimension
Les composants ML tels que les réseaux de neurones profonds contiennent des milliers, voire des millions de paramètres de modèle et de composants bruts. Par exemple, le DNN de pointe utilisé dans la figure 2 comporte jusqu'à 60 millions de paramètres et des dizaines de couches de composants. Cela crée un énorme espace de recherche pour la vérification et le processus d'abstraction doit être très prudent.
Adaptation et évolution en ligne
Certains systèmes d'apprentissage, tels que les robots utilisant RL, évoluent à mesure qu'ils rencontrent de nouvelles données et situations. Pour de tels systèmes, la vérification au moment de la conception doit tenir compte de l'évolution future du comportement du système, ou être effectuée progressivement en ligne à mesure que le système d'apprentissage évolue.
Modélisation de systèmes en contexte
Pour de nombreux composants IA/ML, leur spécification est définie uniquement par le contexte. Par exemple, pour vérifier la sécurité du système basé sur DNN dans la figure 2, il faut modéliser l'environnement. Nous avons besoin de techniques qui modélisent les composants ML et leur contexte afin que les propriétés sémantiquement significatives puissent être vérifiées.
Ces dernières années, de nombreux travaux se sont concentrés sur l'amélioration de l'efficacité pour vérifier la robustesse et les propriétés entrée-sortie du DNN. Cependant, cela ne suffit pas, nous devons également progresser dans les trois aspects suivants :
Abstraction automatique et représentation efficace
L'abstraction des systèmes générés automatiquement a toujours été la clé des méthodes formelles , qui est la clé des méthodes formelles. Les méthodes formelles jouent un rôle crucial dans l'extension de la portée aux grands systèmes matériels et logiciels. Pour relever les défis des espaces d'états mixtes et des espaces d'entrée de très haute dimension pour les systèmes basés sur le ML, nous devons développer des techniques efficaces pour résumer les modèles de ML en modèles plus simples et plus faciles à analyser formellement. Certaines directions prometteuses incluent : l’analyse des DNN à l’aide d’interprétations abstraites, le développement d’abstractions pour fabriquer des systèmes cyber-physiques avec des composants ML et la conception de nouvelles représentations pour la vérification (telles que des ensembles d’étoiles).
Explication et cause à effet
Nous pouvons simplifier la tâche de modélisation des systèmes d'apprentissage si les apprenants accompagnent leurs prédictions d'explications sur la façon dont les prédictions ont émergé des données et des connaissances de base. L’idée n’est pas nouvelle, des termes tels que « généralisation basée sur l’explication » étant déjà recherchés par la communauté du ML, mais plus récemment, on constate un regain d’intérêt pour l’utilisation de la logique pour expliquer les résultats des systèmes d’apprentissage. La génération d’explications aide à déboguer les conceptions et les spécifications au moment de la conception et aide à synthétiser des systèmes d’IA robustes qui fournissent une assurance au moment de l’exécution. Le ML, y compris le raisonnement causal et contrefactuel, peut également aider à générer des explications pour les méthodes formelles.
Semantic Feature Space
L'analyse contradictoire et la vérification formelle des modèles ML sont plus efficaces lorsque les entrées contradictoires et les contre-exemples générés ont une signification sémantique dans le contexte du modèle ML utilisé. Par exemple, les techniques qui analysent un détecteur d'objets DNN pour détecter de petits changements dans la couleur d'une voiture ou l'heure de la journée sont plus utiles que les techniques qui ajoutent du bruit à un petit nombre de pixels choisis arbitrairement. Actuellement, la plupart des méthodes échouent à ce stade. Nous avons besoin d’une analyse contradictoire sémantique, c’est-à-dire d’analyser les modèles ML dans le contexte du système auquel ils appartiennent. Une étape clé consiste à représenter l'espace de fonctionnalités sémantiques qui modélise l'environnement dans lequel le système ML fonctionne, plutôt que l'espace de fonctionnalités spécifique qui définit l'espace d'entrée du modèle ML. Ceci est conforme à l’intuition selon laquelle l’espace latent formé par les parties sémantiquement significatives de l’espace de caractéristiques concret (telles que les images de scènes de trafic) est bien inférieur à celui de l’espace de caractéristiques concret complet. L'espace de fonctionnalités sémantiques de la figure 2 est un espace de faible dimension qui représente le monde 3D autour d'un véhicule autonome, tandis que l'espace de fonctionnalités spécifiques est un espace de pixels de haute dimension. Étant donné que la dimensionnalité de l’espace des caractéristiques sémantiques est plus faible, il peut être recherché plus facilement. Cependant, nous avons également besoin d'un « moteur de rendu » qui mappe un point de l'espace de fonctionnalités sémantiques à un point de l'espace de fonctionnalités concret. Les propriétés du moteur de rendu, telles que la différentiabilité, facilitent l'application de méthodes formelles pour effectuer des recherches orientées vers un objectif dans l'espace des fonctionnalités sémantiques.
Moteurs informatiques pour la conception et la vérification
L'efficacité des méthodes formelles pour les systèmes matériels et logiciels dépend des progrès des « moteurs informatiques » sous-jacents – par exemple, la résolution de satisfaction booléenne (SAT), la théorie modulaire de la satisfaction ( SMT) et vérification de modèle. Compte tenu de l’ampleur des systèmes d’IA/ML, de la complexité de l’environnement et des nouvelles spécifications impliquées, une nouvelle classe de moteurs de calcul est nécessaire pour une formation, des tests, une conception et une validation efficaces et évolutifs, défis clés qui doivent être surmontés pour réaliser ces avancées.
5.1 Conception d'ensembles de données
Les données sont le point de départ de base de l'apprentissage automatique. Pour améliorer la qualité du système ML, vous devez améliorer la qualité des données qu'il apprend. Comment les méthodes formelles peuvent-elles aider à la sélection, à la conception et à l’enrichissement systématiques des données ML ?
La génération de données ML présente des similitudes avec le problème de génération de tests pour le matériel et les logiciels. Les méthodes formelles se sont révélées efficaces pour la génération systématique de tests basés sur des contraintes, mais cela diffère des exigences des systèmes d'intelligence artificielle, où les types de contraintes peuvent être beaucoup plus complexes - par exemple, pour l'utilisation de capteurs pour extraire des données d'environnements complexes tels que comme les conditions de circulation) pour coder les exigences relatives à « l’authenticité » des données capturées. Non seulement nous devons générer des éléments de données avec des caractéristiques spécifiques (telles que des tests qui détectent des bogues), mais nous devons également générer des collections qui satisfont aux contraintes de distribution ; la génération de données doit répondre aux objectifs de taille et de diversité des ensembles de données pour une formation et une généralisation efficaces. Ces exigences nécessitent le développement d’un nouvel ensemble de techniques formelles.
Randomisation contrôlée dans les méthodes formelles. Ce problème de conception d'ensembles de données comporte de nombreux aspects. Premièrement, l'espace des entrées « légitimes » doit être défini afin que les exemples soient correctement formés en fonction de la sémantique de l'application. Deuxièmement, les contraintes sur la mesure de similarité avec les données du monde réel doivent être respectées. être capturé; troisièmement, il est souvent nécessaire de générer La distribution des exemples est contrainte pour obtenir une garantie que l'algorithme d'apprentissage converge vers le vrai concept.
Nous pensons que ces aspects peuvent être abordés par des méthodes formelles stochastiques - des algorithmes stochastiques pour générer des données soumises à des contraintes formelles et à des exigences de distribution. Une nouvelle classe de nouvelles techniques appelées improvisation contrôlée est prometteuse, qui génère des chaînes aléatoires (exemples)
- Une contrainte douce qui définit comment les éléments générés sont générés, nous commençons tout juste à comprendre la complexité informatique et à concevoir des algorithmes efficaces. L'improvisation, quant à elle, s'appuie sur les progrès récents dans les problèmes informatiques tels que l'échantillonnage aléatoire contraint, le comptage de modèles et les méthodes génératives basées sur la programmation probabiliste.
- 5.2 Vérification quantitative
- En plus de mesurer l'échelle des systèmes d'IA à l'aide de métriques traditionnelles (dimensions de l'espace d'état, nombre de composants, etc.), les types de composants peuvent être beaucoup plus complexes . Par exemple, les véhicules autonomes et semi-autonomes et leurs contrôleurs doivent être modélisés comme des systèmes hybrides, combinant des dynamiques discrètes et continues. De plus, les représentants dans l'environnement (humains, autres véhicules) peuvent devoir être modélisés comme des processus probabilistes ; Enfin, les exigences peuvent impliquer non seulement des spécifications booléennes traditionnelles sur la sécurité et l'activité, mais également des exigences quantitatives sur la robustesse et les performances du système. Pourtant, la plupart des méthodes de vérification existantes visent à répondre aux questions de vérification booléennes. Pour combler cette lacune, de nouveaux moteurs évolutifs de validation quantitative doivent être développés.
- Analyse sémantique quantitative. En général, la complexité et l'hétérogénéité des systèmes d'IA signifient que la vérification formelle canonique (booléenne ou quantitative) est indécidable - par exemple, même déterminer si un état d'un système hybride linéaire est accessible est indécidable. Pour surmonter cet obstacle posé par la complexité informatique, il faut utiliser de nouvelles techniques de vérification probabiliste et quantitative sur les espaces de caractéristiques sémantiques afin d'améliorer les approches d'abstraction et de modélisation évoquées plus haut dans cette section. Pour les formalismes canoniques avec une sémantique à la fois booléenne et quantitative, dans des formalismes tels que la logique métrique-temporelle, la formulation de la vérification comme optimisation est cruciale pour unifier les méthodes de calcul des méthodes formelles et les méthodes de calcul de la littérature sur l'optimisation. Par exemple, dans la falsification de la logique temporelle basée sur la simulation, bien qu'elles doivent être appliquées à l'espace des fonctionnalités sémantiques pour plus d'efficacité, de telles techniques de falsification peuvent également être utilisées pour générer systématiquement et de manière contradictoire des données de formation pour les composants ML. Les techniques de vérification probabiliste devraient aller au-delà des formes traditionnelles telles que les chaînes de Markov ou les MDP pour vérifier les programmes probabilistes sur les espaces de fonctionnalités sémantiques. De même, les travaux sur la résolution SMT doivent être étendus pour gérer plus efficacement les contraintes de coûts, en d’autres termes, en combinant la résolution SMT avec des méthodes d’optimisation.
Nous devons comprendre ce qui peut être garanti au moment de la conception, comment le processus de conception contribue à un fonctionnement sûr au moment de l'exécution et comment les technologies au moment de la conception et de l'exécution peuvent interagir efficacement.
5.3 Raisonnement combinatoire pour l'IA/ML
Pour les méthodes formelles permettant d'évoluer vers de grands systèmes, le raisonnement combinatoire (modulaire) est essentiel. Dans la vérification compositionnelle, un grand système (par exemple, un programme) est divisé en ses composants (par exemple, un programme), chaque composant est vérifié par rapport à une spécification, puis les spécifications des composants sont rassemblées pour produire une spécification au niveau du système. Une approche courante de la vérification combinatoire consiste à utiliser des contrats d'hypothèse-garantie. Par exemple, une procédure suppose quelque chose concernant son état de départ (conditions préalables), qui à son tour garantit son état final (postconditions). Un paradigme d'hypothèse-garantie similaire a été utilisé. et appliquer des systèmes logiciels et matériels simultanés.
Cependant, ces paradigmes ne couvrent pas les systèmes d'intelligence artificielle, en grande partie à cause des défis de formalisation des systèmes d'intelligence artificielle abordés dans la section « Spécifications formelles ». La vérification composable nécessite une spécification de composition, c'est-à-dire que les composants doivent être formalisables. Cependant, comme décrit dans « Spécifications formelles », il peut ne pas être possible de spécifier formellement le comportement correct d'un composant perceptuel. Par conséquent, l’un des défis consiste à développer des techniques de raisonnement combinatoire qui ne reposent pas sur une spécification combinatoire complète. De plus, la nature quantitative et probabiliste des systèmes d’IA nécessite d’étendre la théorie du raisonnement combinatoire aux systèmes et spécifications quantitatifs.
Déduire les contrats de composants. La conception et l’analyse combinatoires des systèmes d’IA nécessitent des progrès sur plusieurs fronts. Premièrement, il est nécessaire de s'appuyer sur des travaux préliminaires prometteurs pour développer une théorie pour la conception et la vérification de garanties probabilistes pour l'espace sémantique de ces systèmes. Deuxièmement, de nouvelles techniques de synthèse inductive doivent être conçues pour générer algorithmiquement des contrats d’hypothèse-garantie qui réduisent le fardeau normatif et facilitent le raisonnement combinatoire. Troisièmement, pour traiter des cas tels que la perception où les composants n'ont pas de spécifications formelles précises, nous proposons des techniques pour déduire des contraintes au niveau des composants à partir d'analyses au niveau du système, et utilisons ces contraintes pour concentrer les analyses au niveau des composants, y compris les analyses contradictoires, sur la recherche. la partie « pertinente » de l’espace.
Systèmes intelligents qui sont corrigés au fur et à mesure de leur construction
Dans un monde idéal, la vérification serait intégrée au processus de conception, de sorte que le système est « corrigé au fur et à mesure de sa construction ». Par exemple, la vérification pourrait être entrelacée avec les étapes de compilation/synthèse, en supposant un flux de conception de niveau de transfert de registre (RTL) commun dans les circuits intégrés, et peut-être pourrait-elle être intégrée dans l'algorithme de synthèse pour garantir que la mise en œuvre répond aux spécifications. Pouvons-nous concevoir un processus de conception adapté aux systèmes d’intelligence artificielle qui soit progressivement révisé au cours de la construction ?
6.1 Conception de composants ML basée sur les spécifications
Étant donné une spécification formelle, pouvons-nous concevoir un composant d'apprentissage automatique (modèle) dont il peut être prouvé qu'il satisfait à la spécification ? La conception de ce nouveau composant ML comporte de nombreux aspects : (1) concevoir l'ensemble de données, (2) synthétiser la structure du modèle, (3) générer un ensemble représentatif de fonctionnalités, (4) synthétiser les hyperparamètres et autres choix. des aspects de l'algorithme ML, et (5) des techniques pour automatiser le débogage des modèles ou des spécifications ML en cas d'échec de la synthèse.
Synthèse formelle des composants ML. Des solutions à certains des problèmes répertoriés précédemment apparaissent. Les propriétés peuvent être appliquées aux modèles ML à l'aide de fonctions de perte sémantique ou de robustesse certifiée. Ces techniques peuvent être combinées avec des méthodes telles que la recherche d'architecture neuronale pour générer des modèles DNN correctement construits. Une autre approche est basée sur la théorie émergente de la synthèse inductive formelle, c'est-à-dire la synthèse à partir d'instances de programme qui satisfont à des spécifications formelles. La manière la plus courante de résoudre les problèmes de synthèse inductive formelle consiste à utiliser une approche guidée par un oracle, dans laquelle un apprenant est associé à un oracle qui répond à la requête, comme dans la figure 2 de l'exemple, l'oracle peut être un faussaire qui génère des contre-exemples ; montrer comment le composant d’apprentissage échoue. Violation des spécifications au niveau du système. Enfin, l'utilisation de la preuve de théorème pour garantir l'exactitude des algorithmes utilisés pour entraîner les modèles de ML constitue également une étape importante vers la construction de composants de ML modifiés.
6.2 Conception de système basée sur l'apprentissage automatique
Le deuxième défi est de concevoir un système global contenant des composants d'apprentissage et de non-apprentissage. Plusieurs questions de recherche se sont posées : pouvons-nous calculer les limites de sécurité dans lesquelles les composants ML peuvent être limités au fonctionnement ? Pouvons-nous concevoir un algorithme de contrôle ou de planification qui surmonte les limitations du composant compatible ML qu'il reçoit en entrée ? Pouvons-nous concevoir une théorie de conception combinatoire pour les systèmes d’intelligence artificielle ? Lorsque deux modèles ML sont utilisés pour détecter deux types différents de données de capteur (par exemple, LiDAR et images visuelles) et que chaque modèle répond à ses spécifications sous certaines hypothèses, dans quelles conditions les deux peuvent-ils être utilisés ensemble pour améliorer la fiabilité globale du système ?
Un exemple frappant de progrès dans ce domaine est le travail sur un contrôle sûr basé sur l'apprentissage. Cette approche précalcule une enveloppe de sécurité et utilise des algorithmes d'apprentissage pour régler le contrôleur dans cette enveloppe, ce qui nécessite des techniques pour calculer efficacement ces enveloppes de sécurité sur la base, par exemple, de l'analyse de l'accessibilité. De même, dans le domaine de la sécurité RL, des progrès significatifs ont également été réalisés ; .
Cependant, ceux-ci ne répondent pas pleinement aux défis posés par l'apprentissage automatique en matière de perception et de prédiction - par exemple, un apprentissage par renforcement profond de bout en bout dont la sécurité est prouvée n'a pas encore été réalisé.
6.3 Relier le temps de conception et le temps d'exécution pour une IA résiliente
Comme indiqué dans la section « Modélisation de l'environnement », de nombreux systèmes d'IA fonctionnent dans des environnements qui ne peuvent pas être spécifiés a priori et il y aura donc toujours circonstances dans lesquelles l’exactitude ne peut être garantie. Les technologies qui mettent en œuvre la tolérance aux pannes et la récupération des erreurs au moment de l’exécution jouent un rôle important dans les systèmes d’intelligence artificielle. Nous avons besoin d’une compréhension systématique de ce qui peut être garanti au moment de la conception, de la manière dont le processus de conception contribue au fonctionnement sûr et correct des systèmes d’IA au moment de l’exécution, et de la manière dont les technologies au moment de la conception et d’exécution peuvent interopérer efficacement.
À cet égard, la littérature sur les systèmes tolérants aux pannes et fiables nous fournit la base pour développer des techniques d'assurance d'exécution - c'est-à-dire des techniques de vérification et d'atténuation d'exécution, par exemple, la méthode Simplex fournit un moyen de combiner ; complexe mais simple Une approche qui combine des modules défectueux avec des modules de sauvegarde sécurisés et formellement vérifiés. Plus récemment, des techniques combinant des approches d'assurance de conception et d'exécution ont montré que les composants non vérifiés, y compris ceux basés sur l'IA et le ML, peuvent être intégrés dans des cadres d'assurance d'exécution pour fournir des garanties de fonctionnement sûr. Mais actuellement, celles-ci sont limitées à des classes spécifiques de systèmes, ou nécessitent une conception manuelle de moniteurs d'exécution et de stratégies d'atténuation. D'autres approches telles que la modélisation introspective de l'environnement, les moniteurs basés sur l'intelligence artificielle et la synthèse de stratégies de repli sûres sont à venir. Il y a beaucoup de travail à faire.
L'approche de conception visant à modifier les systèmes intelligents dans la construction évoquée ici peut introduire des frais généraux qui rendent plus difficile le respect des exigences de performances et de temps réel. Mais nous pensons (peut-être de manière non intuitive) que les méthodes formelles peuvent même contribuer à améliorer les performances ou l’efficacité énergétique d’un système dans le sens suivant.
Le réglage traditionnel des performances a tendance à être indépendant du contexte : par exemple, les tâches doivent respecter les délais indépendamment de l'environnement dans lequel elles s'exécutent. Mais si ces environnements sont formellement caractérisés au moment de la conception, surveillés au moment de l'exécution et si le fonctionnement de leur système est formellement vérifié comme étant sûr, alors dans de tels environnements, les modèles de ML peuvent troquer la précision contre une plus grande efficacité. Ce compromis pourrait constituer un domaine fructueux pour de futures recherches.
Conclusion
Du point de vue des méthodes formelles, nous avons disséqué le problème de la conception de systèmes d'intelligence artificielle à haute assurance. Comme le montre la figure 3, nous avons identifié cinq défis majeurs dans l'application de méthodes formelles aux systèmes d'IA et avons développé trois principes de conception et de vérification pour chacun des cinq défis susceptibles de relever ce défi.
Les bords de la figure 3 montrent les dépendances entre ces principes, telles que les garanties d'exécution s'appuyant sur l'introspection et la modélisation d'environnement basée sur les données pour extraire des hypothèses et des modèles d'environnement contrôlables. De même, pour effectuer une analyse au niveau du système, nous devons nous engager dans un raisonnement combinatoire et une abstraction, où certains composants de l'IA peuvent nécessiter des spécifications d'exploration de données tandis que d'autres génèrent la structure correcte via une synthèse inductive formelle.
Plusieurs chercheurs, dont les auteurs, travaillent sur ces défis depuis 2016, lorsque la version originale publiée de cet article présentait quelques exemples de progrès. Nous avons développé des outils open source VerifAI et Scenic qui mettent en œuvre des techniques basées sur les principes décrits dans cet article et ont été appliqués à des systèmes à l'échelle industrielle dans les domaines de la conduite autonome et de l'aérospatiale. Ces résultats ne sont qu’un début et il reste encore beaucoup à faire. L’IA vérifiable devrait continuer à être un domaine de recherche fructueux dans les années à venir.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment ajouter une nouvelle colonne dans SQL
Apr 09, 2025 pm 02:09 PM
Comment ajouter une nouvelle colonne dans SQL
Apr 09, 2025 pm 02:09 PM
Ajoutez de nouvelles colonnes à une table existante dans SQL en utilisant l'instruction ALTER TABLE. Les étapes spécifiques comprennent: la détermination des informations du nom de la table et de la colonne, rédaction des instructions de la table ALTER et exécution des instructions. Par exemple, ajoutez une colonne de messagerie à la table des clients (VARCHAR (50)): Alter Table Clients Ajouter un e-mail VARCHAR (50);
 Quelle est la syntaxe pour ajouter des colonnes dans SQL
Apr 09, 2025 pm 02:51 PM
Quelle est la syntaxe pour ajouter des colonnes dans SQL
Apr 09, 2025 pm 02:51 PM
La syntaxe pour ajouter des colonnes dans SQL est alter table table_name Ajouter Column_name data_type [pas null] [default default_value]; Lorsque Table_Name est le nom de la table, Column_name est le nouveau nom de colonne, DATA_TYPE est le type de données, et non Null Spécifie si les valeurs NULL sont autorisées, et default default_value spécifie la valeur par défaut.
 Comment définir des valeurs par défaut lors de l'ajout de colonnes dans SQL
Apr 09, 2025 pm 02:45 PM
Comment définir des valeurs par défaut lors de l'ajout de colonnes dans SQL
Apr 09, 2025 pm 02:45 PM
Définissez la valeur par défaut des colonnes nouvellement ajoutées, utilisez l'instruction ALTER TABLE: Spécifiez des colonnes Ajouter et définissez la valeur par défaut: alter table table_name Ajouter Column_name data_type default_value; Utilisez la clause CONSTRAINT pour spécifier la valeur par défaut: ALTER TABLE TABLE_NAME ADD COLUMN COLUMN_NAME DATA_TYPE CONSTRAINT DEFAULT_CONSTRAINT DEFAULT_VALUE;
 Tableau Clear SQL: Conseils d'optimisation des performances
Apr 09, 2025 pm 02:54 PM
Tableau Clear SQL: Conseils d'optimisation des performances
Apr 09, 2025 pm 02:54 PM
Conseils pour améliorer les performances de compensation de la table SQL: utilisez une table tronquée au lieu de supprimer, libre d'espace et réinitialiser la colonne d'identité. Désactivez les contraintes de clés étrangères pour éviter la suppression en cascade. Utilisez les opérations d'encapsulation des transactions pour assurer la cohérence des données. Supprimer les mégadonnées et limiter le nombre de lignes via Limit. Reconstruisez l'indice après la compensation pour améliorer l'efficacité de la requête.
 Utilisez la déclaration de suppression pour effacer les tables SQL
Apr 09, 2025 pm 03:00 PM
Utilisez la déclaration de suppression pour effacer les tables SQL
Apr 09, 2025 pm 03:00 PM
Oui, l'instruction Delete peut être utilisée pour effacer une table SQL, les étapes sont les suivantes: Utilisez l'instruction Delete: Delete de Table_Name; Remplacez Table_Name par le nom de la table à effacer.
 Comment ajouter une colonne à une table SQL
Apr 09, 2025 pm 02:06 PM
Comment ajouter une colonne à une table SQL
Apr 09, 2025 pm 02:06 PM
L'ajout d'une colonne dans une table SQL nécessite les étapes suivantes: Ouvrez l'environnement SQL et sélectionnez la base de données. Sélectionnez le tableau que vous souhaitez modifier et utiliser la clause "Ajouter la colonne" pour ajouter une colonne qui inclut le nom de la colonne, le type de données et l'opportunité d'autoriser les valeurs nulles. Exécutez l'instruction "ALTER TABLE" pour terminer l'ajout.
 Comment gérer la fragmentation de la mémoire redis?
Apr 10, 2025 pm 02:24 PM
Comment gérer la fragmentation de la mémoire redis?
Apr 10, 2025 pm 02:24 PM
La fragmentation de la mémoire redis fait référence à l'existence de petites zones libres dans la mémoire allouée qui ne peut pas être réaffectée. Les stratégies d'adaptation comprennent: Redémarrer Redis: effacer complètement la mémoire, mais le service d'interruption. Optimiser les structures de données: utilisez une structure plus adaptée à Redis pour réduire le nombre d'allocations et de versions de mémoire. Ajustez les paramètres de configuration: utilisez la stratégie pour éliminer les paires de valeurs clés les moins récemment utilisées. Utilisez le mécanisme de persistance: sauvegardez régulièrement les données et redémarrez Redis pour nettoyer les fragments. Surveillez l'utilisation de la mémoire: découvrez les problèmes en temps opportun et prenez des mesures.
 phpmyadmin crée un tableau de données
Apr 10, 2025 pm 11:00 PM
phpmyadmin crée un tableau de données
Apr 10, 2025 pm 11:00 PM
Pour créer un tableau de données à l'aide de PhpMyAdmin, les étapes suivantes sont essentielles: connectez-vous à la base de données et cliquez sur le nouvel onglet. Nommez le tableau et sélectionnez le moteur de stockage (InnODB recommandé). Ajouter les détails de la colonne en cliquant sur le bouton Ajouter une colonne, y compris le nom de la colonne, le type de données, s'il faut autoriser les valeurs nuls et d'autres propriétés. Sélectionnez une ou plusieurs colonnes comme clés principales. Cliquez sur le bouton Enregistrer pour créer des tables et des colonnes.






