Fusionnant deux modèles sans aucun obstacle, la connexion linéaire de grands modèles ResNet ne prend que quelques secondes, inspirant de nouvelles recherches sur les réseaux neuronaux

Le deep learning a pu réaliser de tels résultats grâce à sa capacité à résoudre des problèmes d'optimisation non convexes à grande échelle avec une relative facilité. Bien que l'optimisation non convexe soit NP-difficile, certains algorithmes simples, généralement des variantes de la descente de gradient stochastique (SGD), ont montré une efficacité surprenante pour adapter réellement de grands réseaux de neurones.

Dans cet article, plusieurs chercheurs de l'Université de Washington ont écrit "Git Re-Basin: Merging Models modulo Permutation Symmetries". Ils ont étudié l'efficacité déraisonnable de l'algorithme SGD sur les problèmes d'optimisation non convexes de grande dimension dans l'apprentissage profond. . Ils s'inspirent de trois questions :

1. Pourquoi SGD fonctionne bien dans l'optimisation de paysages de perte d'apprentissage profond non convexes de grande dimension, tout en étant robuste dans d'autres paramètres d'optimisation non convexes tels que l'apprentissage des politiques, l'optimisation de trajectoire et la recommandation. systèmes Diminution significative ?

2. Où est le minimum local ? Pourquoi la perte diminue-t-elle de manière douce et monotone lors d'une interpolation linéaire entre les poids d'initialisation et les poids d'entraînement finaux ?

3. Pourquoi deux modèles formés indépendamment avec un ordre d'initialisation aléatoire et de traitement par lots de données différents obtiennent-ils presque les mêmes performances ? De plus, pourquoi leurs courbes de perte d’entraînement se ressemblent-elles ? Variabilité, de sorte que différents entraînements montreront presque les mêmes performances.

Pourquoi cela se produit-il ? En 2019, Brea et al. ont remarqué que les unités cachées dans les réseaux de neurones présentaient une symétrie d'arrangement. En termes simples : nous pouvons échanger deux unités quelconques dans la couche cachée du réseau, et la fonctionnalité du réseau restera la même. Entezari et al. 2021 ont émis l'hypothèse que ces symétries de permutation pourraient nous permettre de connecter linéairement des points dans l'espace de poids sans compromettre les pertes.

Ci-dessous, nous utilisons un exemple de l'un des auteurs de l'article pour illustrer l'objectif principal de l'article, afin que tout le monde le comprenne plus clairement.

Supposons que vous ayez entraîné un modèle A et que votre ami ait entraîné un modèle B, les données d'entraînement des deux modèles peuvent être différentes. Ce n'est pas grave, grâce au Git Re-Basin proposé dans cet article, vous pouvez fusionner les deux modèles A+B dans l'espace poids sans nuire à la perte.

​

Les auteurs de l'article ont déclaré que Git Re-Basin peut être appliqué à n'importe quel réseau neuronal (NN). Ils ont démontré pour la première fois qu'il existe deux modèles formés indépendamment (pas de pré-entraînement). (ResNets), une connectivité linéaire sans obstacle est possible.

Ils ont découvert que la capacité de fusion est une propriété de la formation SGD, la fusion ne fonctionne pas à l'initialisation, mais un changement de phase se produit, donc la fusion deviendra possible avec le temps.

Ils ont également constaté que la largeur du modèle est étroitement liée à la fusion, c'est-à-dire que plus large est mieux.

​

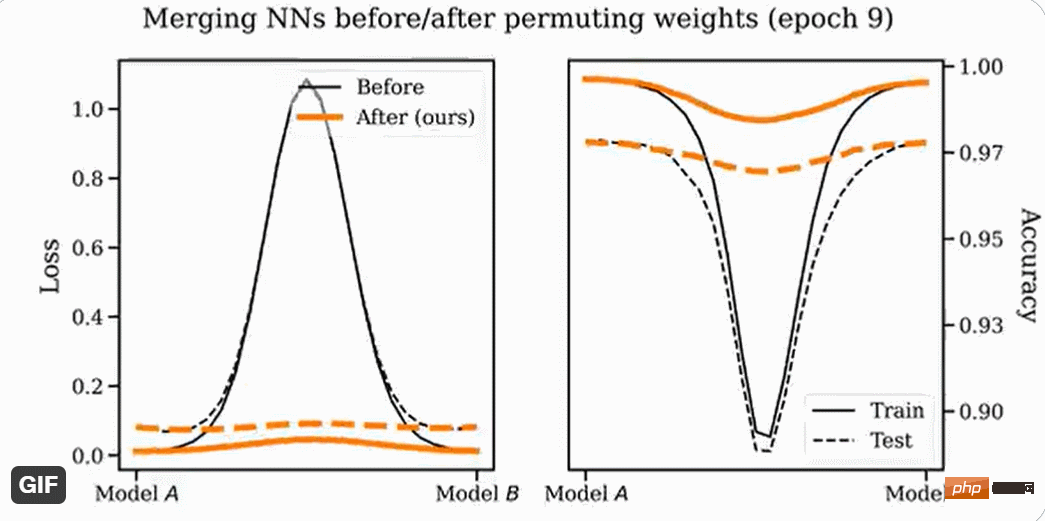
De plus, toutes les architectures ne peuvent pas être fusionnées : VGG semble être plus difficile à fusionner que ResNets.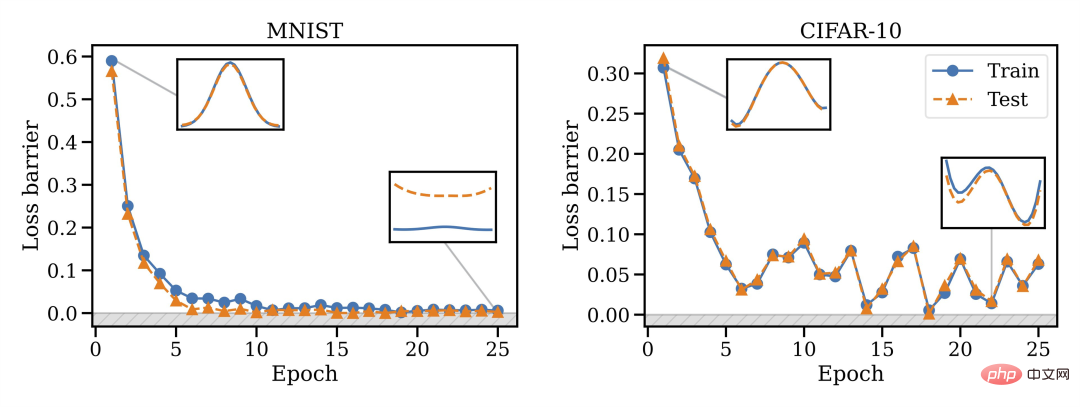

Cette méthode de fusion présente d'autres avantages, vous pouvez entraîner le modèle sur des ensembles de données disjoints et biaisés, puis les fusionner dans l'espace de pondération. Par exemple, vous disposez de certaines données aux États-Unis et d’autres dans l’UE. Pour une raison quelconque, les données ne peuvent pas être mélangées. Vous pouvez d'abord entraîner des modèles distincts, puis fusionner les poids et enfin généraliser à l'ensemble de données fusionné.

​

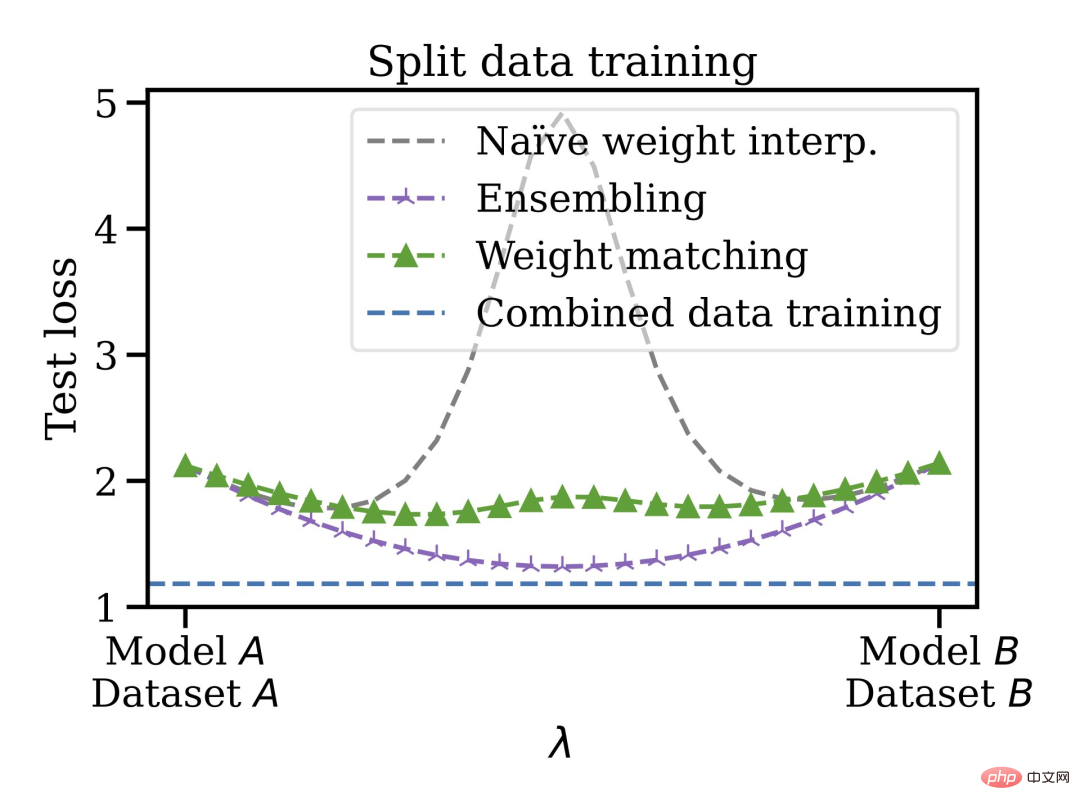
Ainsi, les modèles formés peuvent être mélangés sans avoir besoin de pré-entraînement ou de réglage fin. L'auteur a exprimé son intérêt à connaître l'orientation future du développement de la connexion en mode linéaire et de la réparation de modèles, qui pourraient être appliquées à des domaines tels que l'apprentissage fédéré, la formation distribuée et l'optimisation de l'apprentissage profond.

Enfin, il est mentionné que l'algorithme de correspondance de poids du chapitre 3.2 ne prend que 10 secondes environ à exécuter, ce qui permet de gagner beaucoup de temps. Le chapitre 3 de l'article présente également trois méthodes pour faire correspondre les unités du modèle A et du modèle B. Les amis qui ne connaissent pas bien l'algorithme de correspondance peuvent vérifier l'article original.

Commentaires des internautes et clarifications de l'auteur

Cet article a déclenché une discussion animée sur Twitter, et le co-fondateur de PyTorch, Soumith Chintala, a déclaré que si cette recherche pouvait être déplacée dans un cadre plus large, la direction qu'elle pourrait atteindre serait plus grande. La fusion de deux modèles (y compris les pondérations) peut étendre le développement de modèles ML et peut jouer un rôle énorme dans le co-développement open source de modèles.

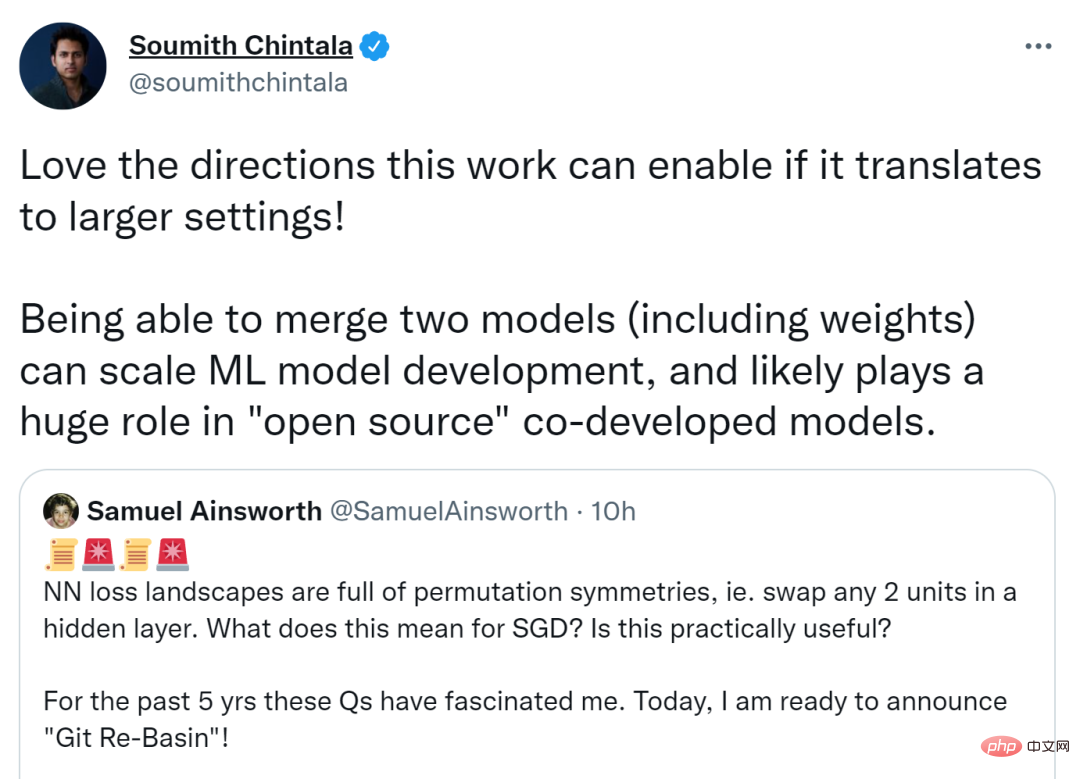
D'autres pensent que si l'invariance par permutation peut capturer la plupart des équivalences avec autant d'efficacité, elle inspirera la recherche théorique sur les réseaux de neurones.

Samuel Ainsworth, premier auteur de l'article et titulaire d'un doctorat de l'Université de Washington, a également répondu à quelques questions soulevées par les internautes.

Tout d'abord, quelqu'un a demandé : "Y a-t-il des conseils dans le document sur le ciblage de bassins uniques lors de l'entraînement ? S'il existait un moyen d'abstraire les permutations, alors l'entraînement pourrait être plus rapide

Ainsworth Il a répondu que." il n'y avait pas pensé. Il espère vraiment pouvoir s’entraîner plus vite d’une manière ou d’une autre, mais jusqu’à présent, cela s’est avéré très difficile. Le problème est que SGD est essentiellement une recherche locale, il n'est donc pas si simple d'exploiter une géométrie d'ordre supérieur. Peut-être que la formation distribuée est la voie à suivre.

​

Certaines personnes ont également demandé si cela était applicable aux RNN et aux Transformers ? Ainsworth dit que cela fonctionne en principe, mais il ne l'a pas encore expérimenté. Le temps nous le dira.

​

Finalement, quelqu'un a demandé : « Cela semble très important pour que la formation distribuée devienne une réalité ? Le DDPM (Denoising Diffusion Probabilistic Model) n'utilise-t-il pas des blocs résiduels ResNet ? »

Ainsworth a répondu que Bien qu'il ne soit pas lui-même très familier avec DDPM, il a déclaré sans ambages que l'utiliser pour une formation distribuée serait très excitant.

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!